| {"year": "2022", "tier": "T2", "problem_label": "1", "problem_type": null, "exam": "EGMO", "problem": "Let $A B C$ be an acute-angled triangle in which $B C<A B$ and $B C<C A$. Let point $P$ lie on segment $A B$ and point $Q$ lie on segment $A C$ such that $P \\neq B, Q \\neq C$ and $B Q=B C=C P$. Let $T$ be the circumcentre of triangle $A P Q, H$ the orthocentre of triangle $A B C$, and $S$ the point of intersection of the lines $B Q$ and $C P$. Prove that $T, H$ and $S$ are collinear.\n\nProposed by: Netherlands", "solution": "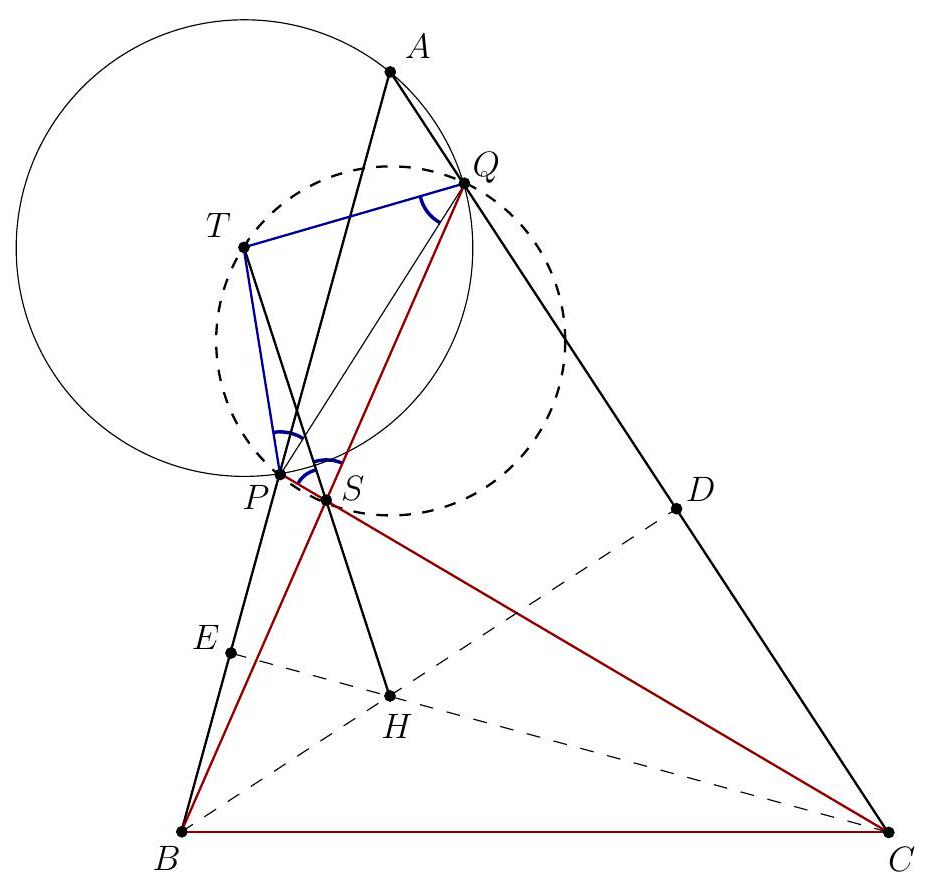\n\nWe show that $T$ and $H$ are both on the angle bisector $\\ell$ of $\\angle B S C$.\nWe first prove that $H \\in \\ell$. The altitude $C H$ in triangle $A B C$ is also the altitude in isosceles triangle $P B C$ with $C P=C B$. Therefore, $C H$ is also the angle bisector of $\\angle P C B$ and hence also of $\\angle S C B$. Analogously, $B H$ is the angle bisector of $\\angle S B C$. We conclude that $H$, as the intersection of two angle bisectors of $\\triangle B S C$, is also on the third angle bisector, which is $\\ell$.\n\nWe now prove that $T \\in \\ell$.\nVariant 1. In the isosceles triangles $\\triangle B C P$ and $\\triangle C B Q$ we see that $\\angle B C P=180^{\\circ}-2 \\angle B$ and $\\angle C B Q=180^{\\circ}-2 \\angle C$. This yields $\\angle P S Q=\\angle B S C=180^{\\circ}-\\left(180^{\\circ}-2 \\angle B\\right)-\\left(180^{\\circ}-2 \\angle C\\right)=$ $180^{\\circ}-2 \\angle A$. Furthermore, $\\angle P T Q=2 \\angle P A Q=2 \\angle A$ ( $T$ being circumcentre of $\\left.\\triangle A P Q\\right)$. Now $\\angle P T Q+\\angle P S Q=180^{\\circ}$, so $P T Q S$ is a cyclic quadrilateral. From $P T=T Q$ we then obtain that $\\angle P S T=\\angle P Q T=\\angle Q P T=\\angle Q S T$, so $T$ is on the angle bisector $\\angle P S Q$, which is also $\\ell$.\n\nWe conclude that $T, S$ and $H$ are collinear.\nVariant 2. Let $R$ be the second intersection of $B Q$ and $\\odot A P Q$.\n$A P R Q$ is cyclic quadrilateral, so $\\angle P R S=\\angle A, \\angle A P R=\\angle B Q C=\\angle C$. On the other hand $\\angle B P C=\\angle B$. Therefore $\\angle R P S=180^{\\circ}-\\angle B-\\angle C=\\angle A$. Hence, the triangle $P R S$ is isosceles with $S P=S R$; then $\\ell$ is the perpendicular bisector of the chord $P R$ in the circle that passes through $T$.\n\nNote that if $B Q$ is tangent to $\\odot A P Q$, then $C P$ is also tangent to $\\odot A P Q$ and triangle $A B C$ is isosceles, so $T, S$ and $H$ lie on the altitude from $A$.\n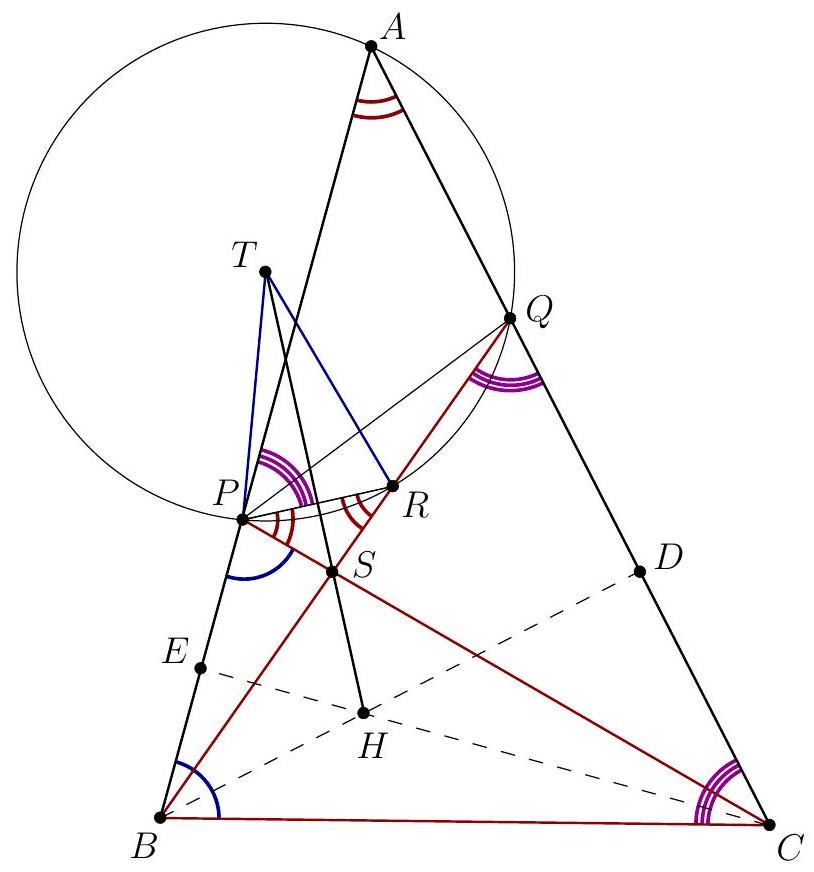\n\nRemark. The fact that $C P$ is also tangent to $\\odot A P Q$ could be shown with $P T Q S$ beeing a cyclic quadrilateral like in the first variant of the solution. Otherwise we can consider $R$ the second intersection of $C P$ and $\\odot A P Q$ and prove that triangle $Q R S$ is isosceles.\n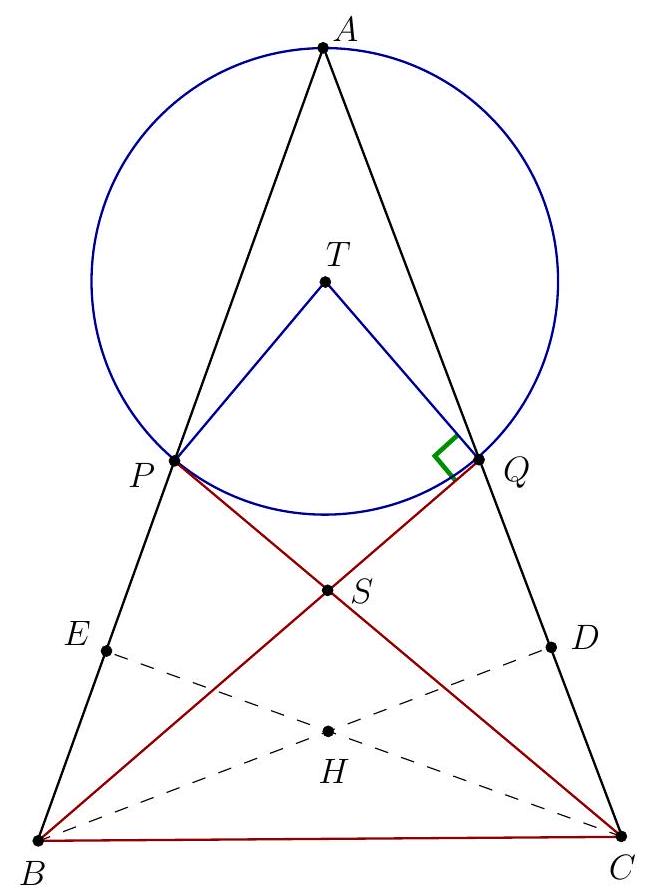\n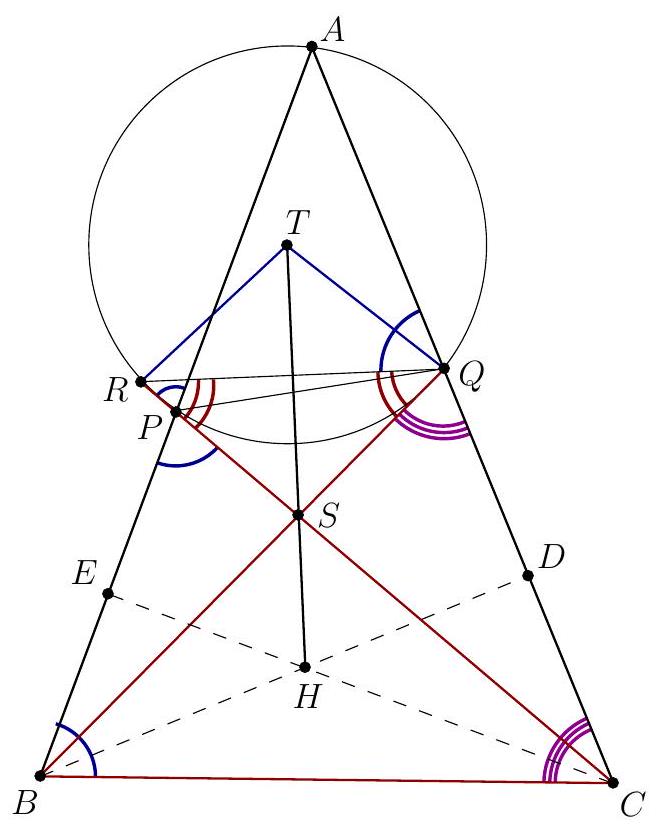", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 1.", "solution_match": "# Solution 1."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "1", "problem_type": null, "exam": "EGMO", "problem": "Let $A B C$ be an acute-angled triangle in which $B C<A B$ and $B C<C A$. Let point $P$ lie on segment $A B$ and point $Q$ lie on segment $A C$ such that $P \\neq B, Q \\neq C$ and $B Q=B C=C P$. Let $T$ be the circumcentre of triangle $A P Q, H$ the orthocentre of triangle $A B C$, and $S$ the point of intersection of the lines $B Q$ and $C P$. Prove that $T, H$ and $S$ are collinear.\n\nProposed by: Netherlands", "solution": "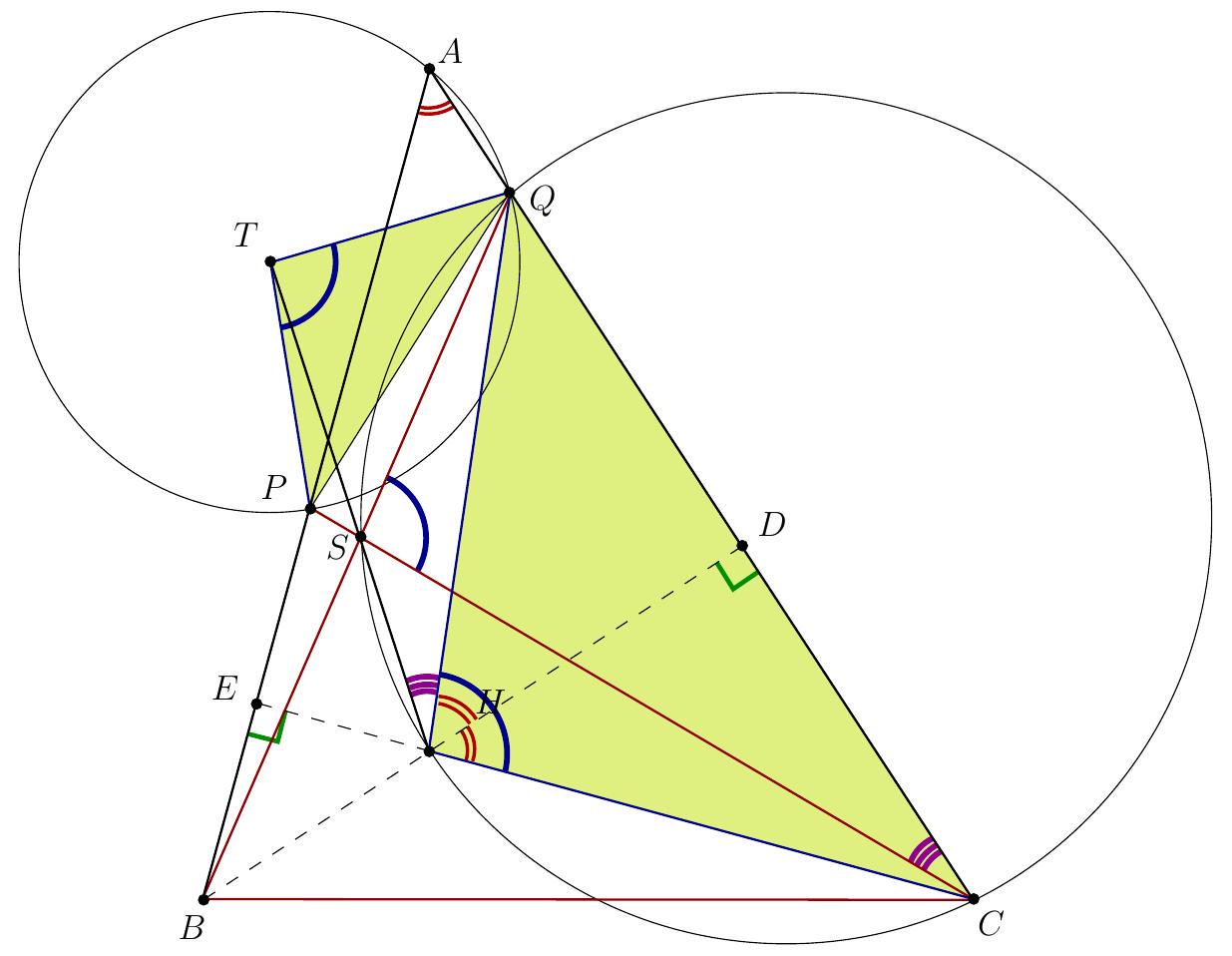\n\nIn the same way as in the previous solution, we see that $\\angle P S Q=180^{\\circ}-2 \\angle A$, so $\\angle C S Q=2 \\angle A$. From the cyclic quadrilateral $A E H D$ (with $E$ and $D$ feet of the altitudes $C H$ and $B H$ ) we see that $\\angle D H C=\\angle D A E=\\angle A$. Since $B H$ is the perpendicular bisector of $C Q$, we have $\\angle D H Q=\\angle A$ as well, so $\\angle C H Q=2 \\angle A$. From $\\angle C H Q=2 \\angle A=\\angle C S Q$, we see $C H S Q$ is a cyclic quadrilateral. This means $\\angle Q H S=\\angle Q C S$.\n\nSince triangles $P T Q$ and $C H Q$ are both isosceles with apex $2 \\angle A$, we get $\\triangle P T Q \\sim \\triangle C H Q$. We see that one can be obtained from the other by a spiral similarity centered at $Q$, so we also obtain $\\triangle Q T H \\sim \\triangle Q P C$. This means that $\\angle Q H T=\\angle Q C P$. Combining this with $\\angle Q H S=\\angle Q C S$, we see that $\\angle Q H T=\\angle Q C P=\\angle Q C S=\\angle Q H S$. So $\\angle Q H T=\\angle Q H S$, which means that $T, S$ and $H$ are collinear.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 1.", "solution_match": "# Solution 2."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "1", "problem_type": null, "exam": "EGMO", "problem": "Let $A B C$ be an acute-angled triangle in which $B C<A B$ and $B C<C A$. Let point $P$ lie on segment $A B$ and point $Q$ lie on segment $A C$ such that $P \\neq B, Q \\neq C$ and $B Q=B C=C P$. Let $T$ be the circumcentre of triangle $A P Q, H$ the orthocentre of triangle $A B C$, and $S$ the point of intersection of the lines $B Q$ and $C P$. Prove that $T, H$ and $S$ are collinear.\n\nProposed by: Netherlands", "solution": "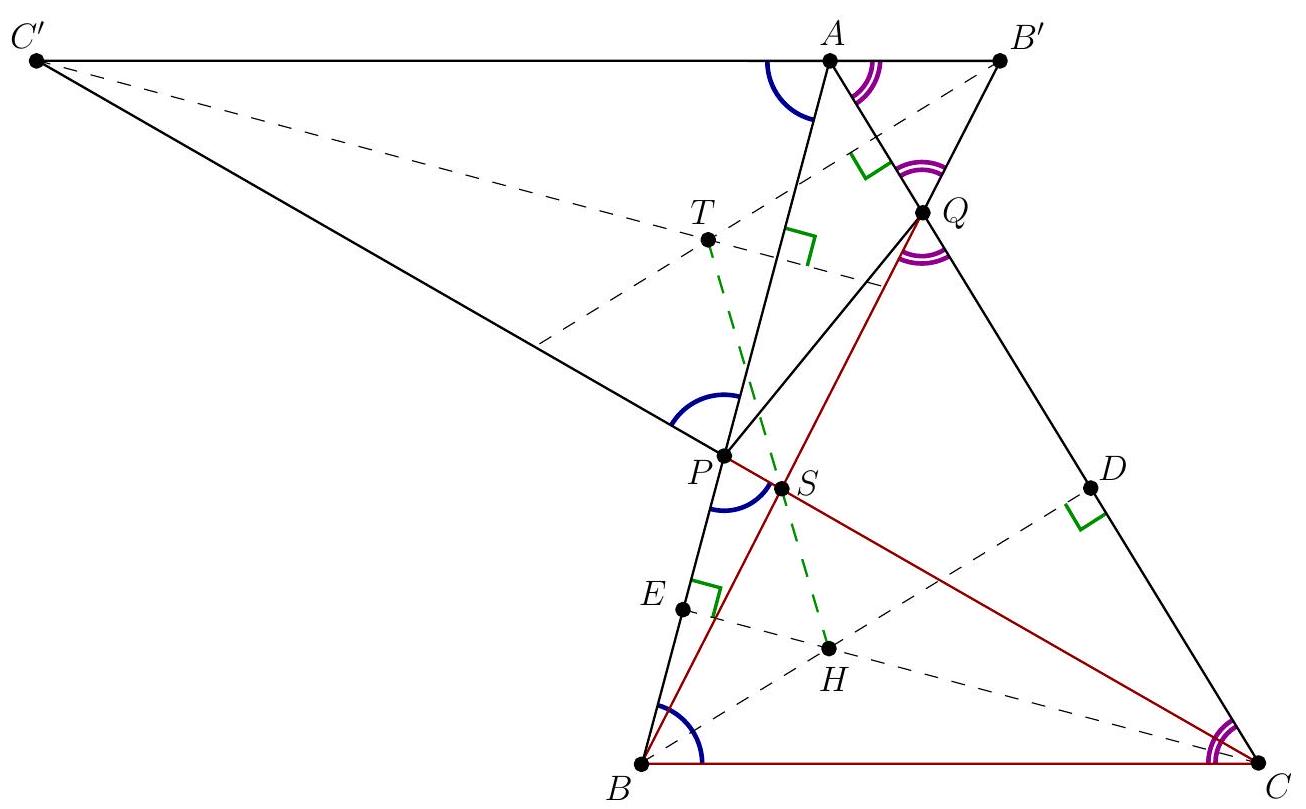\n\nLet us draw a parallel $f$ to $B C$ through $A$. Let $B^{\\prime}=B Q \\cap f, C^{\\prime}=C P \\cap f$. Then $A Q B^{\\prime} \\sim C Q B$ and $A P C^{\\prime} \\sim B P C$, therefore both $Q A B^{\\prime}$ and $A P C^{\\prime}$ will be isosceles.\n\nAlso, $B C S \\sim B^{\\prime} C^{\\prime} S$ with respect to the similarity with center $S$, therefore if we take the image of the line $B H$ (which is the perpendicular bisector of the segment $C Q$ ) through this transformation, it will go through the point $B^{\\prime}$, and be perpendicular to $A Q$ (as the image of $C Q$ is parallel to $C Q$ ). As $A Q B^{\\prime}$ is isosceles, this line is the perpendicular bisector of the segment $A Q$. This means it goes through $T$, the circumcenter of $A P Q$. Similarly on the other side the image of $C H$ also goes through $T$. This means that the image of $H$ with respect to the similarity though $S$ will be $T$, so $T, S, H$ are collinear.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 1.", "solution_match": "# Solution 3."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "First, all such functions $f$ satisfy the conditions, as $v_{p}(a) \\neq v_{p}(b)$ implies $v_{p}(a+b)=$ $\\min \\left(v_{p}(a), v_{p}(b)\\right)$. Plugging $a, b=1$ into (1) gives $f(1)=1$. Also, a simple induction gives that $f\\left(\\prod_{i=1}^{k} p_{i}^{a_{i}}\\right)=\\prod_{i=1}^{k} f\\left(p_{i}\\right)^{a_{i}}$. Let $S$ be the set of all primes $p$ such that $f(p) \\neq 1$. If $|S|=1$, then $S=\\{p\\}$ and $f(p)=a$ for some $a \\neq 1$, and thus $f(n)=a^{v_{p}(n)}$ for all $n$. If $S=\\emptyset$ then $f(n)=1$ for all $n$, which can be also written in the above form for $a=1$.\n\nNow suppose that $S$ contains at least two primes. Let $p<q$ be the two smallest elements of $S$. Since all prime divisors of $q-p$ are smaller than $q$ and not equal to $p, f(q-p)=1$. Using (2) for $p$ and $q-p$ gives us that some two of $f(p) \\neq 1, f(p-q)=1$ and $f(q) \\neq 1$ are equal, meaning that $f(p)=f(q)$. Let $t \\geq 2$ be the smallest integer such that $p^{t}>q$, and let $p^{t}=a q+b$ with $0 \\leq b<q$. Since $q \\geq p^{t-1}$ and $q$ is not divisible by $p$, we have $q>p^{t-1}$, so $a<p$, and thus $f(a)=1$. Therefore $a q$ is not divisible by $p$, thus neither is $b$, and since $b<q, f(b)=1$. Now using (2) for $a q$ and $b$ we get that some two of $f(a q)=f(a) f(q)=f(q)=f(p), f(b)=1$ and $f(a q+b)=f\\left(p^{t}\\right)=f(p)^{t}$ are equal, which is a contradiction.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution 1. "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "1B (for the main part).\n\nSuppose that there are two primes, $p<q$ such that $f(p)>1$ and $f(q)>1$, and these are the two smallest such primes.\n$1<p-q<q$ and it is not divisible by $p$ and $q$, therefore its prime factors are smaller than $q$, so we conclude $f(q-p)=1$. By (2), two of $f(q-p)=1, f(q-p)>1$ and $f(q)>1$ are equal, so $f(q)=f(p)=a$.\n\nIf $p^{2}<q$ then $q-p^{2}$ is not divisible by $p$ and $q$, so we conclude $f\\left(q-p^{2}\\right)=1$ in the same way. Then $f\\left(p^{2}\\right)=f(p)^{2}=a^{2}, f\\left(q-p^{2}\\right)=1$ and $f(q)=a$ are distinct, contradicting (2). Hence, $q<p^{2}$.\n\nLet $c=\\left\\lfloor p^{2} / q\\right\\rfloor$; then $0<c<p$, so $f(c)=1$. By $0<p^{2}-c q<q$, we get $f\\left(p^{2}-c q\\right)=1$. Now $f\\left(p^{2}-c q\\right)=1, f\\left(p^{2}\\right)=a^{2}$ and $f(c q)=a$ are distinct, contradicting (2) again.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "# Solution "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "Suppose there exists a positive integer $n$ such that $f(n) \\neq 1$ and $f(n+1) \\neq 1$. We know that $f(1)=1$, so by $(2)$ two of $f(n) \\neq 1, f(n+1) \\neq 1$ and $f(1)=1$ are equal, therefore $f(n)=f(n+1)$.\n$f\\left(n^{2}\\right)=f(n)^{2} \\neq 1$ and $f\\left(n^{2}-1\\right)=f(n+1) f(n-1)=f(n) f(n-1) \\neq 1$, but by (2) two of $f(1)=1, f\\left(n^{2}-1\\right) \\neq 1$ and $f\\left(n^{2}\\right) \\neq 1$ are equal, so $f\\left(n^{2}-1\\right)=f\\left(n^{2}\\right)$ and thus $f(n) f(n-1)=f(n)^{2}$, therefore $f(n-1)=f(n)$.\n\nThen for $n-1$, it is also true that $f(n-1) \\neq 1$ and $f(n-1+1) \\neq 1$, so the same proof applies, $f(n-1-1)=f(n-1)$ and so on. By induction we get that $f(n)=f(1)$, which is a contradiction, as $f(1)=1$ and we assumed that $f(n) \\neq 1$. Therefore, there can't be any $n$ for which $f(n) \\neq 1$ and $f(n+1) \\neq 1$.\n\nNow suppose there are two primes, $p \\neq q \\in S$ such that $f(p) \\neq 1$ and $f(q) \\neq 1$. Then by the Chinese remainder theorem, there exists a number $n$ such that $p \\mid n$ and $q \\mid n+1$, so $f(p) \\mid f(n)$ and $f(q) \\mid f(n+1)$ thus $f(n) \\neq 1$ and $f(n+1) \\neq 1$. This is a contradiction, so $S$ can't have two distinct elements.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "# Solution 2 (for the main part)."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "(for the second part).\n\nClaim 3.1. If $f(m)>1$ for some $m \\in \\mathbb{N}$, then there are less than $m$ different prime numbers $p_{i}$ with $f\\left(p_{i}\\right)>1$.\nProof. On the one hand, if $f(m)=c>1$, then for any $n \\in \\mathbb{N}$, there is some $k \\in\\{n+1, n+2 \\ldots, n+m\\}$ such that $f(k) \\in\\{1, c\\}$. To show this, it is enough to see that condition (2) implies that for any $n \\in \\mathbb{N}$\n\n- if $f(n)=c$, then $f(n+1) \\in\\{1, c\\}$;\n- if $f(n)=1$, then $f(n+m) \\in\\{1, c\\}$.\n\nOn the other hand, if we suppose that there are $m$ different prime numbers $p_{1}, p_{2}, \\ldots, p_{m}$, then we know (by the Chinese Remainder Theorem) that for any number $t \\in \\mathbb{N}$, there exists a number $n_{t} \\in \\mathbb{N}$ such that $p_{k}^{t} \\mid n_{t}+k$ for each $k \\in\\{1,2, \\ldots, m\\}$. Hence for each $k$, we have\n\n$$\nf\\left(n_{t}+k\\right) \\geq f\\left(p_{i}^{t}\\right)=f\\left(p_{i}\\right)^{t} \\geq 2^{t} .\n$$\n\nIf $2^{t}>c$, then it means that $f(k)>c$ for all $k \\in\\left\\{n_{t}+1, n_{t}+2 \\ldots, n_{t}+m\\right\\}$.\nNow we can suppose that for some $m \\geq 2$, the set of primes with $f(p)>1$ is $S=\\left\\{p_{1}, p_{2}, \\ldots, p_{m}\\right\\}$. Now let $S_{1}$ and $S_{2}$ be two disjoint nonempty subsets such that $S_{1} \\cup S_{2}=S$. Let $a=\\prod_{p_{i} \\in S_{1}} p_{i}$ and $b=\\prod_{p_{j} \\in S_{2}} p_{j}$.\n\nNow for any $k, \\ell \\in \\mathbb{N}, a^{k}+b^{\\ell}$ is coprime to all primes in $S$, hence $f\\left(a^{k}+b^{\\ell}\\right)=1$. It is easy to see that we can choose $k$ and $\\ell$ such that $f\\left(a^{k}\\right) \\neq f\\left(b^{\\ell}\\right)$, which contradicts condition (2).", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "# Solution 3 (Joseph Myers) "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "Let $p$ the minimal (prime) number with $f(p)=c>1$.\nClaim 4.1. For any $k \\in \\mathbb{N}, f\\left(1+p+p^{2}+\\ldots+p^{k}\\right) \\in\\left\\{1, c, c^{2}, \\ldots, c^{k}\\right\\}$.\nProof of the claim. Use condition (2) recursively.\nNow suppose that there exists some prime $q>p$ with $f(q)>1$, and consider the following three values of $f$ :\n\n- $f(1)=1$.\n- $f\\left(p^{q-1}-1\\right)=f(p-1) f\\left(p^{q-2}+p^{q-3}+\\ldots+p+1\\right) \\in\\left\\{1, c, c^{2}, \\ldots, c^{q-2}\\right\\}$ using our claim, (note that we know $f(p-1)=1$ by the minimality of $p$ ).\nBut we also know (by Fermat's little theorem) that $q \\mid p^{q-1}-1$, hence $f(q) \\mid f\\left(p^{q-1}-1\\right)$. Therefore we have that: $f\\left(p^{q-1}-1\\right) \\in\\left\\{c, c^{2}, \\ldots, c^{q-2}\\right\\}$.\n- $f\\left(p^{q-1}\\right)=c^{q-1}$.\n\nThese are three different values, hence we have a contradiction by condition (2).", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution 4 (for the main part)."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "4B (for the main part). Let $p$ the minimal (prime) number with $f(p)=c>1$.\nLemma 4B.1. For any $k \\in \\mathbb{N}, f\\left(1+p+p^{2}+\\ldots+p^{k}\\right)=1$.\nProof of the Lemma, by induction. $k=0$ is trivial.\n$k=1$ is also easy, as $p+1$ cannot be a prime, except in the case of $p=2$, which is also easy. (If $f(2)=c>1$, then $f(3) \\in\\{1, c\\}$ by $3=1+2$ and $f(3) \\in\\left\\{1, c^{2}\\right\\}$ by $2^{2}=1+3$.)\n\nFrom now we suppose $k \\geq 2$ and $f\\left(1+p+\\ldots+p^{k-1}\\right)=1$. By condition (2), we have that:\n\n- As $f\\left(1+p+\\ldots+p^{k-1}\\right)=1$ and $f\\left(p^{k}\\right)=c^{k}$, we have that $f\\left(1+p+\\ldots+p^{k-1}\\right) \\in\\left\\{1, c^{k}\\right\\}$\n- As $f(1)=1$ and $f\\left(p+\\ldots+p^{k}\\right)=f(p) f\\left(1+p+\\ldots+p^{k-1}\\right)=c$, we also have that $f\\left(1+p+\\ldots+p^{k-1}\\right) \\in\\{1, c\\}$.\nIf $k>1, c \\neq c^{k}$, therefore $f\\left(1+p+\\ldots+p^{k}\\right)=1$.\n\nNow suppose that there exists some prime $q>p$ with $f(q)>1$. Then by condition (1),\n\n$$\nf\\left(p^{q-1}-1\\right)=f(p-1) f\\left(1+p+\\ldots+p^{q-2}\\right)\n$$\n\nhere $f(p-1)=1$ (by the minimality of $p$ ) and $f\\left(1+p+\\ldots+p^{q-2}\\right)=1$ by the lemma. But we also know (by Fermat's little theorem) that $q \\mid p^{q-1}-1$, hence $1<f(q) \\leq f\\left(p^{q-1}-1\\right.$ ), which is a contradiction.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "\nSolution "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "2", "problem_type": null, "exam": "EGMO", "problem": "Let $\\mathbb{N}=\\{1,2,3, \\ldots\\}$ be the set of all positive integers. Find all functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for any positive integers $a$ and $b$, the following two conditions hold:\n(1) $f(a b)=f(a) f(b)$, and\n(2) at least two of the numbers $f(a), f(b)$ and $f(a+b)$ are equal.\n\nProposed by: Fedir Yudin, Ukraine\nAnswer: $f(n)=a^{v_{p}(n)}$, where $a \\in \\mathbb{N}, p$ is a prime and $v_{p}(n)$ is the largest exponent of $p$ dividing $n$.", "solution": "Lemma 5.1. If $f(m) \\neq f(n)$, then $f(n+m)=f(n-m)$ (for all $n>m \\in \\mathbb{N}$ ).\nProof of the Lemma. By condition (2), $\\{f(n+m), f(n-m)\\} \\subseteq\\{f(n), f(m)\\}$. We also have that:\n\n$$\nf(n-m) f(n+m)=f\\left(n^{2}-m^{2}\\right) \\in\\left\\{f(n)^{2}, f(m)^{2}\\right\\}\n$$\n\nwhich is only possible if $f(n-m)=f(n+m)=f(n)$ or $f(n-m)=f(n+m)=f(m)$.\nNow let $p$ be the smallest (prime) number with $f(p)>1$.\nClaim 5.2. If $p$ does not divide $n$, then $f(n)=1$.\nProof of the Claim. Let $n$ be the minimal counterexample, and and let $n=d p+r$ with $0<r<p$. Here $d \\geq 1$ by the minimality of $p$.\n\nNow $1<f(d) f(p)=f(d p) \\neq f(r)=1$, hence by our lemma, $f(d p+r)=f(d p-r)=1$, contradiction.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 2.", "solution_match": "# Solution 5 (for the main part)."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "3", "problem_type": null, "exam": "EGMO", "problem": "An infinite sequence of positive integers $a_{1}, a_{2}, \\ldots$ is called good if\n(1) $a_{1}$ is a perfect square, and\n(2) for any integer $n \\geq 2, a_{n}$ is the smallest positive integer such that\n\n$$\nn a_{1}+(n-1) a_{2}+\\ldots+2 a_{n-1}+a_{n}\n$$\n\nis a perfect square.\nProve that for any good sequence $a_{1}, a_{2}, \\ldots$, there exists a positive integer $k$ such that $a_{n}=a_{k}$ for all integers $n \\geq k$.\n\nProposed by: Joe Benton and Dominic Yeo, United Kingdom", "solution": "Define the following auxiliary sequences:\n\n$$\n\\begin{array}{ll}\nb_{1}=a_{1}, & b_{n}=a_{1}+a_{2}+\\cdots+a_{n} \\\\\nc_{1}=b_{1}, & c_{n}=b_{1}+b_{2}+\\cdots+b_{n}\n\\end{array}\n$$\n\nObserve that\n\n$$\n\\begin{gathered}\nc_{n}-c_{n-1}=b_{n} \\\\\nb_{n}-b_{n-1}=\\left(c_{n}-c_{n-1}\\right)-\\left(c_{n-1}-c_{n-2}\\right)=a_{n}\n\\end{gathered}\n$$\n\nTherefore,\n\n$$\nc_{n}=\\left(2 c_{n-1}-c_{n-2}\\right)+a_{n}\n$$\n\nis the smallest square greater than $2 c_{n-1}-c_{n-2}$.\nClaim. $\\sqrt{c_{n}}-\\sqrt{c_{n-1}} \\leq \\sqrt{c_{n-1}}-\\sqrt{c_{n-2}}$\nProof 1. Let $c_{n}=m_{n}^{2}, c_{n-1}=m_{n-1}^{2}, c_{n-2}=m_{n-2}^{2}$, where the value of $c_{n}$ is momentarily permitted to exceed its minimum. Any value is permitted for which\n\n$$\nb_{n}=c_{n}-c_{n-1}>b_{n-1}=c_{n-1}-c_{n-2}\n$$\n\nFactoring,\n\n$$\n\\left(m_{n}-m_{n-1}\\right)\\left(m_{n}+m_{n-1}\\right)>\\left(m_{n-1}-m_{n-2}\\right)\\left(m_{n-1}+m_{n-2}\\right)\n$$\n\nIn the case that $m_{n}-m_{n-1}=m_{n-1}-m_{n-2}$, this inequality clearly holds, as $m_{n}+m_{n-1}>m_{n-1}+m_{n-2}$. Thus, the minimal possible value of $m_{n}$ satisfies the claimed inequality.\n\nProof 2. Denote $c_{n-1}=x^{2}, c_{n-2}=(x-d)^{2}$. Then\n\n$$\n2 c_{n-1}-c_{n-2}=2 x^{2}-(x-d)^{2}=x^{2}+2 d x-d^{2}=(x+d)^{2}-2 d^{2}<(x+d)^{2}\n$$\n\nIt follows that $c_{n} \\leq(x+d)^{2}$.\nAnd so the sequence of positive integers $\\sqrt{c_{n}}-\\sqrt{c_{n-1}}$ is decreasing. Any such sequence is eventually constant.\n\nAs a corollary, $c_{n}=(x+n d)^{2}$ for sufficiently large $n$, with fixed integers $x$ and $d$. Along the lines above, it becomes clear that $a_{n}=c_{n}-2 c_{n-1}+c_{n-2}=2 d^{2}$, so the sequence $\\left(a_{n}\\right)$ is constant.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "3", "problem_type": null, "exam": "EGMO", "problem": "An infinite sequence of positive integers $a_{1}, a_{2}, \\ldots$ is called good if\n(1) $a_{1}$ is a perfect square, and\n(2) for any integer $n \\geq 2, a_{n}$ is the smallest positive integer such that\n\n$$\nn a_{1}+(n-1) a_{2}+\\ldots+2 a_{n-1}+a_{n}\n$$\n\nis a perfect square.\nProve that for any good sequence $a_{1}, a_{2}, \\ldots$, there exists a positive integer $k$ such that $a_{n}=a_{k}$ for all integers $n \\geq k$.\n\nProposed by: Joe Benton and Dominic Yeo, United Kingdom", "solution": "We write:\n\n$$\ns_{n}^{2}=S_{n}=a_{1}+\\left(a_{1}+a_{2}\\right)+\\ldots+\\left(a_{1}+\\ldots+a_{n}\\right)\n$$\n\nSo, setting $b_{n}:=a_{1}+\\ldots+a_{n}$, we have $S_{n}=b_{1}+b_{2}+\\ldots+b_{n}$ and, in particular $S_{n+1}=S_{n}+b_{n+1}$. Now, we study the quantity $S_{n} b_{n}=+b_{1}+b_{2}+\\ldots+b_{n}+b_{n}$ in two different ways. Since $b_{n+1}$ is the smallest integer strictly greater than $b_{n}$ such that $b_{1}+\\ldots+b_{n}+b_{n+1}$ is a perfect square, we must have\n\n$$\nb_{1}+b_{2}+\\ldots+b_{n}+b_{n} \\geq\\left(s_{n+1}-1\\right)^{2}\n$$\n\nHowever, we also have\n\n$$\nb_{1}+b_{2}+\\ldots+b_{n}+b_{n}=S_{n}+b_{n}=2 S_{n}-S_{n-1}\n$$\n\nCombining, we obtain\n\n$$\ns_{n}^{2} \\geq \\frac{s_{n-1}^{2}+\\left(s_{n+1}-1\\right)^{2}}{2}>\\left(\\frac{s_{n-1}+s_{n+1}-1}{2}\\right)^{2}\n$$\n\nwhere the final inequality is strict since the sequence $\\left(s_{k}\\right)$ is strictly increasing. Taking a square root, and noting that all the $\\left(s_{n}\\right)$ are integers, one obtains $s_{n+1}-s_{n} \\leq s_{n}-s_{n-1}$.\nNow we focus on the sequence $d_{n}=s_{n+1}-s_{n} .\\left(s_{k}\\right)$ is strictly increasing thus $\\left(d_{k}\\right)$ is positive. However we proved that $d_{n+1} \\leq d_{n}$, so the sequence $\\left(d_{k}\\right)$ is eventually constant, so eventually $s_{n}=b n+c$ and $S_{n}=(b n+c)^{2}$ with some numbers $b, c$; then\n\n$$\na_{n+2}=S_{n+2}-2 S_{n+1}+S_{n}=(b(n+2)+c)^{2}-2(b(n+1)+c)^{2}+(b n+c)^{2}=2 b^{2}\n$$\n\nRemark. The key idea is to use the $D$ difference operator on the space of sequences. That is a function which takes a sequence as an input and outputs another sequence the following way: if $(x)$ is the input sequence, then\n\n$$\nD(x)=D\\left(\\left(x_{1}, x_{2}, x_{3}, x_{4}, \\ldots\\right)\\right)=\\left(x_{2}-x_{1}, x_{3}-x_{2}, x_{4}-x_{3}, \\ldots\\right)\n$$\n\nHere $D D(S)=(a)$ (with some shift), $D(s)=(d)$. This $D$ operator has some nice properties; if someone studied calculus, these properties will be familiar. $D(x+y)=D(x)+D(y) ; D(\\lambda x)=\\lambda D(x) ;(x)$ constant iff $D x$ zero ; $(x)$ is linear iff $D x$ constant ; in general $(x)$ is a polynomial with degree $l+1$ iff $D(x)$ is a polynomial with degree $l$.\n\nFirst we proved that sequence $(d)$ is eventually constant, thus $D(d)=D D(s)$ is eventually zero. Therefore the sequence $(s)$ is eventually a linear function, hence $s^{2}=S$ is eventually a quadratic polynomial, therefore $0=D D D(S)=D(a)$, so $(a)$ is constant eventually.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 3.", "solution_match": "\nSolution."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "4", "problem_type": null, "exam": "EGMO", "problem": "Given a positive integer $n \\geq 2$, determine the largest positive integer $N$ for which there exist $N+1$ real numbers $a_{0}, a_{1}, \\ldots, a_{N}$ such that\n(1) $a_{0}+a_{1}=-\\frac{1}{n}$, and\n(2) $\\left(a_{k}+a_{k-1}\\right)\\left(a_{k}+a_{k+1}\\right)=a_{k-1}-a_{k+1}$ for $1 \\leq k \\leq N-1$.\n\nProposed by: Romania", "solution": "$\\left(a_{k}+a_{k-1}\\right)\\left(a_{k}+a_{k+1}\\right)=a_{k-1}-a_{k+1}$ is equivalent to $\\left(a_{k}+a_{k-1}+1\\right)\\left(a_{k}+a_{k+1}-1\\right)=-1$. Let $b_{k}=a_{k}+a_{k+1}$. Thus we need $b_{0}, b_{1}, \\ldots$ the following way: $b_{0}=-\\frac{1}{n}$ and $\\left(b_{k-1}+1\\right)\\left(b_{k}-1\\right)=-1$. There is a proper sequence $b_{0}, b_{1}, \\ldots, b_{N-1}$ if and only if there is proper sequence $a_{0}, a_{1}, \\ldots, a_{N}$, because from a a proper $\\left(a_{k}\\right)$ sequence we can get a proper $\\left(b_{k}\\right)$ sequence with $b_{k}=a_{k}+a_{k+1}$ for $k=0,1, \\ldots, N-1$ and from a proper $\\left(b_{k}\\right)$ sequence we can get a proper $\\left(a_{k}\\right)$ sequence by arbitrarily setting $a_{0}$ and then inductively defining $a_{k}=b_{k-1}-a_{k-1}$ for $k=1,2, \\ldots, N$.\n\nWe prove by induction that $b_{k}=-\\frac{1}{n-k}$ for $k<n$. This is true for $k=0$, as $b_{0}=-\\frac{1}{n}$ and\n\n$$\nb_{k}=1-\\frac{1}{b_{k-1}+1}=1-\\frac{1}{1-\\frac{1}{n-k+1}}=-\\frac{1}{n-k}\n$$\n\nfor $k<n$. Thus there is a proper sequence $b_{0}, b_{1}, \\ldots, b_{n-1}$, but it can't be continued, because $b_{n-1}+1=$ 0 so there is no $b_{n}$ for which $\\left(b_{n-1}+1\\right)\\left(b_{n}-1\\right)=-1$.\n\nTherefore the longest proper sequence $\\left(b_{k}\\right)$ is $n$-long, so the longest proper sequence $\\left(a_{k}\\right)$ is $n+1$ long, so $N=n$.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 4.", "solution_match": "\nSolution 1. "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "4", "problem_type": null, "exam": "EGMO", "problem": "Given a positive integer $n \\geq 2$, determine the largest positive integer $N$ for which there exist $N+1$ real numbers $a_{0}, a_{1}, \\ldots, a_{N}$ such that\n(1) $a_{0}+a_{1}=-\\frac{1}{n}$, and\n(2) $\\left(a_{k}+a_{k-1}\\right)\\left(a_{k}+a_{k+1}\\right)=a_{k-1}-a_{k+1}$ for $1 \\leq k \\leq N-1$.\n\nProposed by: Romania", "solution": "The required maximum is $N=n$.\nTo rule out the case $N \\geq n+1$, it is clearly sufficient to rule out the case $N=n+1$.\nAssume for contradiction that $a_{0}, a_{1}, \\ldots, a_{n+1}$ are real numbers satisfying both conditions in the statement. It is sufficient to show that $a_{k}+a_{k+1}=0$ for some $k \\leq n$, because then $a_{k-1}-a_{k+1}=0$ so $a_{k+1}=a_{k-1}$, therefore $a_{k-1}+a_{k}=0$ and so on, by backwards recursion we get that $a_{j}+a_{j+1}=0$ for all $0 \\leq j \\leq k$, but this is a contradiction with $a_{0}+a_{1}=-\\frac{1}{n}$.\n\nTo prove that $a_{k}+a_{k+1}=0$ for some $k \\leq n$, assume that $a_{k}+a_{k+1} \\neq 0$ for all $k \\leq n$, to rewrite the second condition in the statement in the form\n\n$$\n\\frac{1}{a_{k}+a_{k+1}}-\\frac{1}{a_{k-1}+a_{k}}=1, \\quad k=1, \\ldots, n\n$$\n\nand sum both sides over the full range from $k=1$ to $n$. This gives\n\n$$\n\\frac{1}{a_{n}+a_{n+1}}-\\frac{1}{a_{0}+a_{1}}=n \\text {. }\n$$\n\nAs $a_{0}+a_{1}=-\\frac{1}{n}$, this means that $\\frac{1}{a_{n}+a_{n+1}}=0$, which is a contradiction. Consequently, $N \\leq n$.\nTo provide $n+1$ real numbers satisfying both conditions in the statement, fix $a_{0}$ and go through the telescoping procedure above to obtain\n\n$$\na_{k}=(-1)^{k} a_{0}+\\sum_{j=1}^{k} \\frac{(-1)^{k-j+1}}{n-j+1}, \\quad k=1, \\ldots, n\n$$\n\nThis concludes the proof.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 4.", "solution_match": "\nSolution 2. "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "5", "problem_type": null, "exam": "EGMO", "problem": "For all positive integers $n, k$, let $f(n, 2 k)$ be the number of ways an $n \\times 2 k$ board can be fully covered by $n k$ dominoes of size $2 \\times 1$. (For example, $f(2,2)=2$ and $f(3,2)=3$.)\nFind all positive integers $n$ such that for every positive integer $k$, the number $f(n, 2 k)$ is odd.\nProposed by: U.S.A.", "solution": "The integers $n$ with the requested property are exactly the ones of the form $2^{k}-1$.\nIn what follows, let $f(m, n)$ denote the number of domino tilings of an $m \\times n$ grid. (For convenience, we also allow $m$ and $n$ to be 0 , in which case $f(m, n)=1$.)\nClaim. $f(m, 2 n+1) \\equiv f(m, n)(\\bmod 2)$ for all $n$ and even $m$\nProof. Consider reflecting $m \\times(2 n+1)$ tilings across the central column. In this way, the tilings are grouped into singletons and pairs, so modulo $2, f(m, 2 n+1)$ is congruent to the number of singletons.\n\nIf a tiling is invariant under reflection in the central column, then every domino with one cell in that column must have both cells in that column.\n\nIn other words, the central column is filled with $\\frac{m}{2}$ vertical dominoes, splitting the remainder of the grid into two $m \\times n$ grids. Obeying the symmetry constraint, there are $f(m, n)$ tilings: each of the tilings of the left grid fixes the tiling of the right grid.\n\nClaim. $f(n, n) \\equiv 0(\\bmod 2)$ for all even $n \\geq 2$. (Recall that $f(0,0)=1$ is odd.)\nProof. Consider reflecting $n \\times n$ tilings across the diagonal. This groups the tilings into pairs, (no tiling is grouped with itself). Hence the number of $n \\times n$ tilings is even.\n\nWe are ready to complete the solution.\n\n- If $n$ is odd, the first claim shows that $n$ satisfies the property if and only if $\\frac{1}{2}(n-1)$ does.\n- If $n \\geq 2$ is even, the second claim shows that $n$ does not satisfy the property.\n- If $n=0$, then $n$ satisfies the property, as $f(m, 0)=1$ always.\n\nThis concludes the proof that the sought numbers are the ones of the form $2^{k}-1$.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 5.", "solution_match": "\nSolution."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "5", "problem_type": null, "exam": "EGMO", "problem": "For all positive integers $n, k$, let $f(n, 2 k)$ be the number of ways an $n \\times 2 k$ board can be fully covered by $n k$ dominoes of size $2 \\times 1$. (For example, $f(2,2)=2$ and $f(3,2)=3$.)\nFind all positive integers $n$ such that for every positive integer $k$, the number $f(n, 2 k)$ is odd.\nProposed by: U.S.A.", "solution": "Color the board as a chessboard. Consider the bipartite graph whose vertices are the squares and the neighbors are connected by an edge. Notice that a domino tiling described in the problem corresponds to a perfect matching in this bipartite graph, so we are interested in the number of perfect matchings.\n\nAnd that is the permanent of the (bipartite) adjacency matrix. However we need to compute it $\\bmod 2\\left(\\right.$ over $\\left.F_{2}\\right)$, so that is the determinant of that matrix.\n\nSo our goal is to decide whether the determinant is 0 or $1 \\bmod 2$, or in other world, that matrix is singular or not. From now we compute everything mod 2. Now we understand what does it mean, that a vector $v$ is in the nullspace (has eigenvalue 0 ). But each entry of $v$ is $0-1$, so in other words we choose a subset of the black squares ( $v$ is the characteristic vector of that subset). So in the language of the board, there is a nontrivial $v$ in the nullspace iff we have a subspace of black square such a way that each white square has even number of black chosen neighbors.\n\nIf $n$ is even, then we can choose a subset such a way in the $n \\times n$ square: the diagonal.\nNow we prove similar connection between $n$ and $2 n+1$ : there is a construction for $n$ iff we have one for $2 n+1 . k$ is always even. If we have a construction in $n \\times k$ then we have one in $(2 n+1) \\times k$ : we mirror the construction to the middle row.\nNow we prove that from a construction in $(2 n+1) \\times k$ we can make a construction in $n \\times k$. First, we\ndon't have any chosen black square in the middle row. Then the chosen black squares in the upper (or lower) $n \\times k$ rectangle is a construction for $n \\times k$. Second, we have some chosen black square in the middle row. Because we can find a white square in the middle row such that is has only one chosen black neighbor in the middle row. Thus this construction isn't symmetric to the horizontal line the symmetric difference of the construction and its reflection (to the vertical line) is a nontrivial vector in the nullspace, thus we can use the first case.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 5.", "solution_match": "# Solution 2."}} | |
| {"year": "2022", "tier": "T2", "problem_label": "6", "problem_type": null, "exam": "EGMO", "problem": "Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$. Let the internal angle bisectors at $A$ and $B$ meet at $X$, the internal angle bisectors at $B$ and $C$ meet at $Y$, the internal angle bisectors at $C$ and $D$ meet at $Z$, and the internal angle bisectors at $D$ and $A$ meet at $W$. Further, let $A C$ and $B D$ meet at $P$. Suppose that the points $X, Y, Z, W, O$ and $P$ are distinct.\n\nProve that $O, X, Y, Z$ and $W$ lie on the same circle if and only if $P, X, Y, Z$ and $W$ lie on the same circle.\n\nProposed by: Ethan Tan, Australia", "solution": "Let $\\Omega$ be the circumcircle of the quadrilateral $A B C D$ and let $r$ be its radius.\nFirst, notice that the points $X, Y, Z, W$ are concyclic. Indeed, using oriented (modulo $180^{\\circ}$ ) angles,\n\n$$\n\\angle(X W, X Y)+\\angle(Z Y, Z W)=\\angle(X A, X B)+\\angle(Z C, Z D)=-\\frac{\\angle A+\\angle B}{2}-\\frac{\\angle C+\\angle D}{2}=0 .\n$$\n\nLet $\\omega$ be the circle passing through these four points. Our goal is to prove that $O \\in \\omega$ occurs if and only if $P \\in \\omega$.\n\nNext, we rule out the case when $A B C D$ is a trapezium. Suppose that if $A B C D$ is an isosceles trapezium; without loss of generality say $A B \\| C D$. By symmetry, points $X, Z, O$ and $P$ lie on the symmetry axis (that is, the common perpendicular bisector of $A B$ and $C D$ ), therefore they are collinear. By the conditions of the problem, these four points are distinct and $X$ and $Z$ are on $\\omega$, so neither $O$, nor $P$ can lie on $\\omega$; therefore the problem statement is obvious. From now on we assume that $A B \\nVdash C D$ and $B C \\nVdash A D$.\n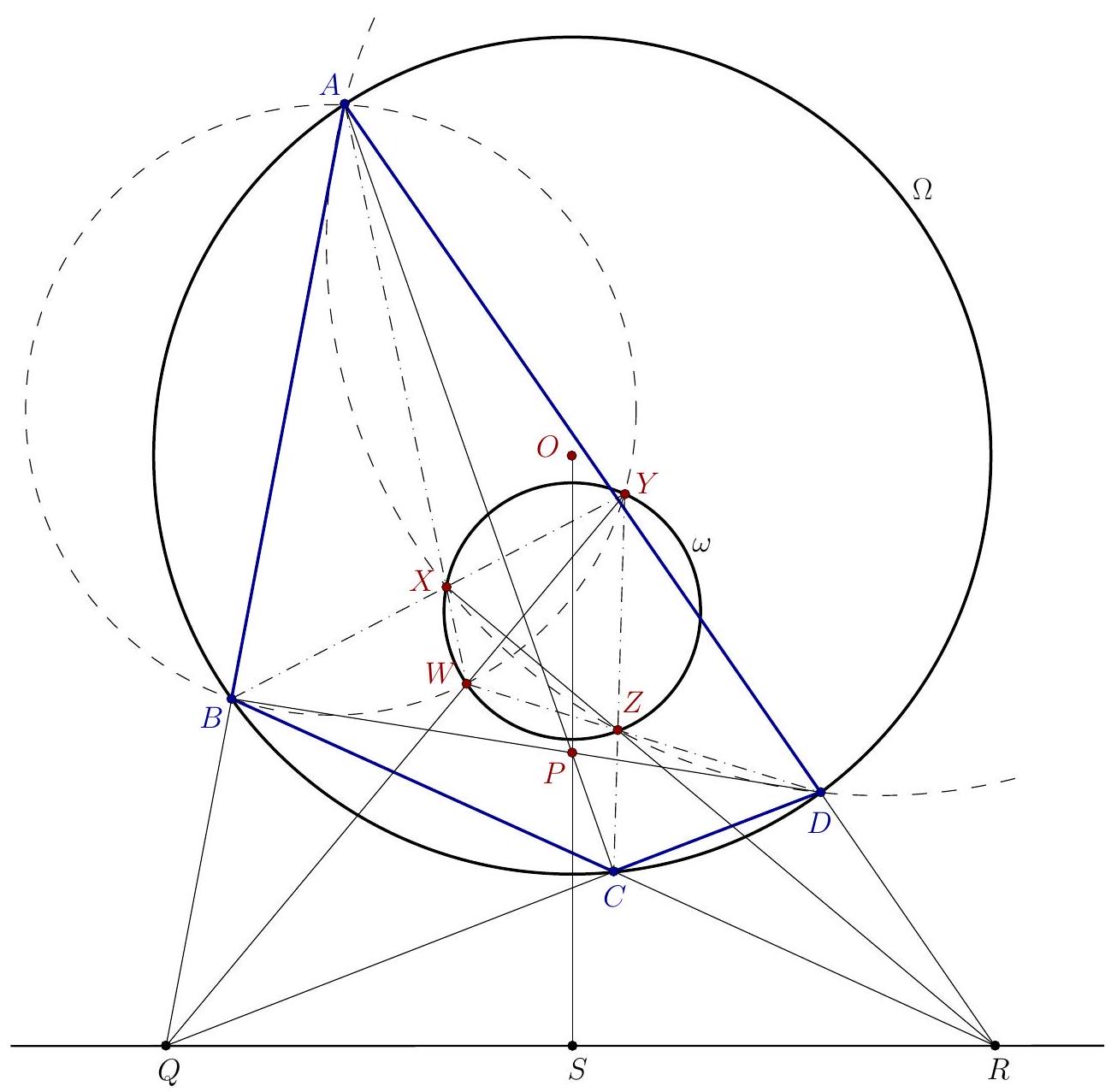\n\nLet $A B$ and $C D$ meet at $Q$, and let $B C$ and $A D$ meet at $R$. Without loss of generality, suppose that $B$ lies between $A$ and $Q$, and $D$ lies between $A$ and $R$. Now we show that line $Q R$ is the radical axis between circles $\\Omega$ and $\\omega$.\n\nPoint $W$ is the intersection point of the bisectors of $\\angle A$ and $\\angle D$, so in triangle $A D Q$, point $W$ is the incentre. Similary, $B Y$ and $C Y$ are the external bisectors of $\\angle Q B C$ and $\\angle B C Q$, so in triangle $B C Q$, point $Y$ is the excentre opposite to $Q$. Hence, both $Y$ and $W$ lie on the bisector of $\\angle D Q A$.\n\nBy $\\angle D Q A=180^{\\circ}-\\angle D-\\angle A=\\angle B-\\angle A$ we get\n\n$$\n\\angle B Y Q=\\angle Y B A-\\angle Y Q B=\\frac{\\angle B}{2}-\\frac{\\angle D Q A}{2}=\\frac{\\angle B}{2}-\\frac{\\angle B-\\angle A}{2}=\\frac{\\angle A}{2}=\\angle B A W\n$$\n\nso the points $A, B, Y, W$ are concyclic, and therefore $Q A \\cdot Q B=Q Y \\cdot Q W$; hence, $Q$ has equal power with respect to $\\Omega$ and $\\omega$. It can be seen similarly that $R$ has equal power with respect to the circles $\\Omega$ and $\\omega$. Hence, the radical axis of $\\Omega$ and $\\omega$ is line $Q R$.\n\nLet lines $O P$ and $Q R$ meet at point $S$. It is well-known that with respect to circle $A B C D$, the diagonal triangle $P Q R$ is autopolar. As consequences we have $O P \\perp Q R$, and the points $P$ and $S$ are symmetric to circle $A B C D$, so $O S \\cdot O P=r^{2}$.\n\nNotice that $P$ and $O$ lie inside $\\Omega$, so the polar line $Q R$ lies entirely outside, so $S$ is different from $P$ and $O$. Moreover,\n\n$$\nS O \\cdot S P=O S \\cdot(O S-O P)=O S^{2}-O S \\cdot O P=S O^{2}-r^{2}\n$$\n\nso $S O \\cdot S P$ is equal to the power of $S$ with respect to $\\Omega$. Since $S$ lies on the radical axis $Q R$, it has equal power with respect to the two circles; therefore, $S O \\cdot S P$ is equal to the power of $S$ with respect to $\\omega$. From this, it follows that $O \\in \\omega$ if and only if $P \\in \\omega$.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 6.", "solution_match": "\nSolution 1. "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "6", "problem_type": null, "exam": "EGMO", "problem": "Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$. Let the internal angle bisectors at $A$ and $B$ meet at $X$, the internal angle bisectors at $B$ and $C$ meet at $Y$, the internal angle bisectors at $C$ and $D$ meet at $Z$, and the internal angle bisectors at $D$ and $A$ meet at $W$. Further, let $A C$ and $B D$ meet at $P$. Suppose that the points $X, Y, Z, W, O$ and $P$ are distinct.\n\nProve that $O, X, Y, Z$ and $W$ lie on the same circle if and only if $P, X, Y, Z$ and $W$ lie on the same circle.\n\nProposed by: Ethan Tan, Australia", "solution": "We will prove that the points $X, Y, Z, W, O, P$ lie on a conic section $\\Gamma$. Five distinct points uniquely determine a conic section, therefore\n\n$$\nX, Y, Z, W, O \\text { are concyclic } \\Leftrightarrow \\Gamma \\text { is a circle } \\Leftrightarrow X, Y, Z, W, P \\text { are concyclic. }\n$$\n\n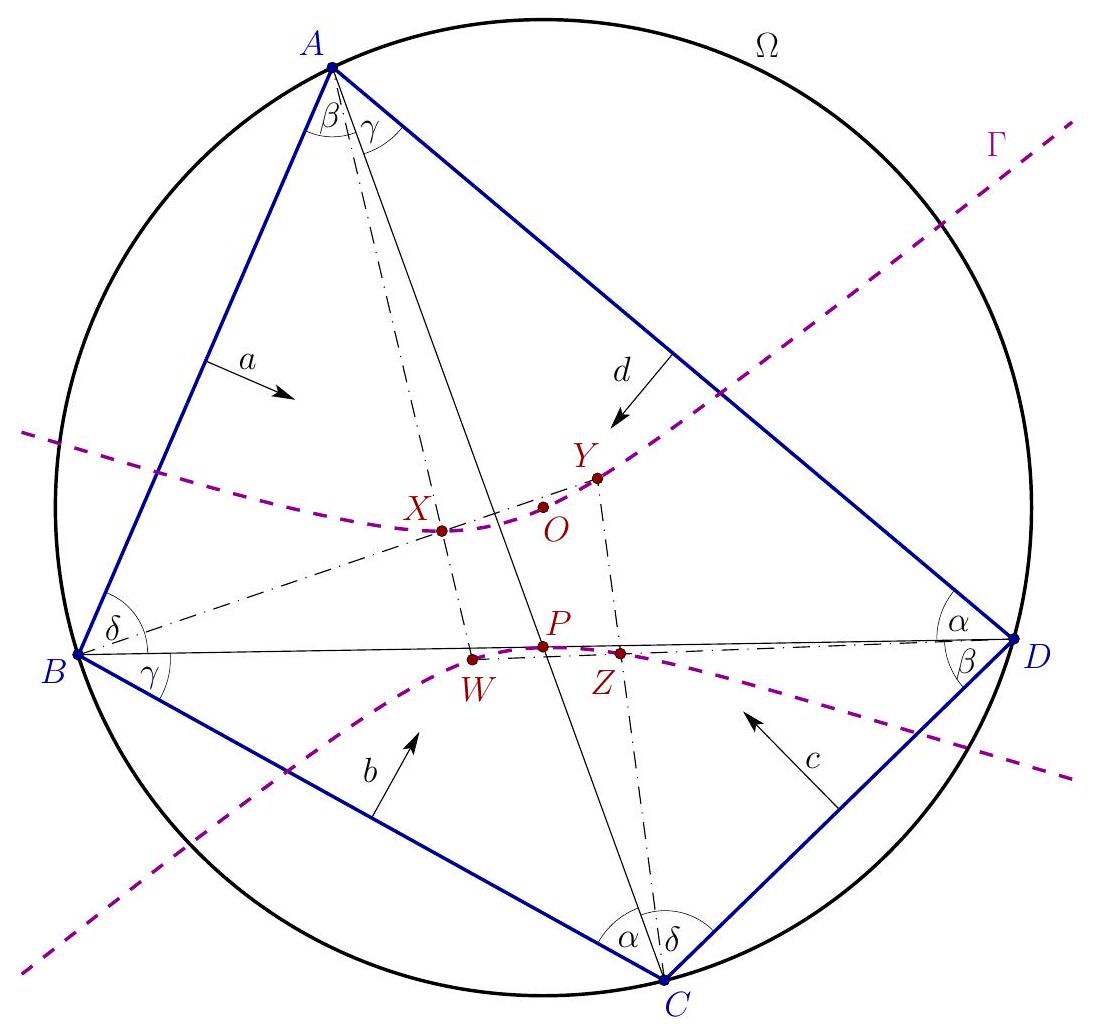\n\nLet $\\alpha=\\angle A C B=\\angle A D B, \\beta=\\angle B D C=\\angle B A C, \\gamma=\\angle C A D=\\angle C B D$ and $\\delta=\\angle D B A=$ $\\angle D C A$, where of course $\\alpha+\\beta+\\gamma+\\delta=180^{\\circ}$. For every point $\\xi$ in the plane, let $a(\\xi), b(\\xi), c(\\xi)$ and $d(\\xi)$ be the signed distances between $\\xi$ and the lines $A B, B C, C D$ and $D A$, respectively, such that the quadrilateral lies on the positive sides of these lines.\n\nThe equations of the bisectors of $\\angle A X W, \\angle B X Y, \\angle C Y Z$ and $\\angle D Z W$ are $a(\\xi)-d(\\xi)=0$, $b(\\xi)-a(\\xi)=0, c(\\xi)-b(\\xi)=0$ and $d(\\xi)-c(\\xi)=0$, respectively. Notice that the points $X, Y, Z, W$ satisfy the quadratic equations $(a(\\xi)-d(\\xi))(b(\\xi)-c(\\xi))=0$ and $(a(\\xi)-b(\\xi))(c(\\xi)-d(\\xi))=0$, so\n\n$$\na(\\xi) b(\\xi)+c(\\xi) d(\\xi)=a(\\xi) c(\\xi)+b(\\xi) d(\\xi)=a(\\xi) d(\\xi)+b(\\xi) c(\\xi) \\quad \\text { for } \\xi=X, Y, Z, W\n$$\n\nWithout loss of generality, suppose that $A B C D$ is inscribed in a unit circle. Then\n\n$$\na(O)=\\cos \\alpha, \\quad b(O)=\\cos \\beta, \\quad c(O)=\\cos \\gamma, \\quad d(O)=\\cos \\delta\n$$\n\nBy $\\frac{a(P)}{b(P)}=\\frac{B P \\cdot \\sin \\delta}{B P \\cdot \\sin \\gamma}=\\frac{1 / \\sin \\gamma}{1 / \\sin \\delta}$ and the analogous relations we can see that\n\n$$\na(P)=\\frac{k}{\\sin \\gamma}, \\quad b(P)=\\frac{k}{\\sin \\delta}, \\quad c(P)=\\frac{k}{\\sin \\alpha}, \\quad d(P)=\\frac{k}{\\sin \\beta}\n$$\n\nwith some positive number $k$.\nNow let $s=\\frac{\\sin \\alpha \\sin \\beta \\sin \\gamma \\sin \\delta}{k^{2}}$; then, by (2a) and (2b),\n\n$$\n\\begin{aligned}\na(O) b(O)-s \\cdot a(P) b(P) & =\\cos \\alpha \\cos \\beta-\\sin \\alpha \\sin \\beta=\\cos (\\alpha+\\beta) \\\\\nc(O) d(O)-s \\cdot c(P) d(P) & =\\cos (\\gamma+\\delta)=-\\cos (\\alpha+\\beta) \\\\\na(O) b(O)+c(O) d(O) & =s \\cdot(a(P) b(P)+c(P) d(P))\n\\end{aligned}\n$$\n\nanalogous calculation provides\n\n$$\n\\begin{aligned}\n& a(O) c(O)+b(O) d(O)=s \\cdot(a(P) c(P)+b(P) d(P)) \\\\\n& a(O) d(O)+b(O) c(O)=s \\cdot(a(P) d(P)+b(P) c(P))\n\\end{aligned}\n$$\n\nIn order to find the equation of the curve $\\Gamma$, choose real numbers $u, v, w$, not all zero, such that\n\n$$\n\\begin{gathered}\nu+v+w=0 \\\\\nu \\cdot(a(P) b(P)+c(P) d(P))+v \\cdot(a(P) c(P)+b(P) d(P))+w \\cdot(a(P) d(P)+b(P) c(P))=0\n\\end{gathered}\n$$\n\nThis is always possible, because this a system of two homogeneous linear equations with three variables. Then the equation of $\\Gamma$ will be\n\n$$\nf(\\xi)=u \\cdot(a(\\xi) b(\\xi)+c(\\xi) d(\\xi))+v \\cdot(a(\\xi) c(\\xi)+b(\\xi) d(\\xi))+w \\cdot(a(\\xi) d(\\xi)+b(\\xi) c(\\xi))=0\n$$\n\nAs can be seen, $f(X)=f(Y)=f(Z)=f(W)=0$ follows from (1) and (4), $f(P)=0$ follows from (5), then $f(O)=s \\cdot f(P)=0$ follows from $(3 a-3 c)$. So, the points $X, Y, Z, W, O, P$ all satisfy the equation $f(\\xi)=0$.\n\nNotice that $f(B)=u \\cdot c(B) d(B)$ and $f(A)=w \\cdot b(A) c(A)$; since at least one of $u$ and $w$ is nonzero, either $A$ or $B$ does not satisfy $(*)$. Therefore, the equation cannot degenerate to an identity.\n\nHence, the equation $f(\\xi)=0$ is at most quadratic, it is not an identity, but satisfied by $X, Y, Z, W, O, P$, so these six points lie on a conic section.", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 6.", "solution_match": "\nSolution 2. "}} | |
| {"year": "2022", "tier": "T2", "problem_label": "6", "problem_type": null, "exam": "EGMO", "problem": "Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$. Let the internal angle bisectors at $A$ and $B$ meet at $X$, the internal angle bisectors at $B$ and $C$ meet at $Y$, the internal angle bisectors at $C$ and $D$ meet at $Z$, and the internal angle bisectors at $D$ and $A$ meet at $W$. Further, let $A C$ and $B D$ meet at $P$. Suppose that the points $X, Y, Z, W, O$ and $P$ are distinct.\n\nProve that $O, X, Y, Z$ and $W$ lie on the same circle if and only if $P, X, Y, Z$ and $W$ lie on the same circle.\n\nProposed by: Ethan Tan, Australia", "solution": "Let $A^{\\prime}, B^{\\prime}, C^{\\prime}$ and $D^{\\prime}$ be the second intersection of the angle bisectors of $\\angle D A C$, $\\angle A B C, \\angle B C D$ and $\\angle C D A$ with the circumcircle of $A B C D$, respectively. Notice that $A^{\\prime}$ and $C^{\\prime}$ are the midpoints of the two arcs of $B D$ and $B^{\\prime}$ and $D^{\\prime}$ are the midpoints of arcs corresponding to $A C$ so the lines $A^{\\prime} C^{\\prime}$ and $B^{\\prime} D^{\\prime}$ intersect in $O$.\n\n\nWe will prove that the points $X, Y, Z, W, P$ and $O$ lie on a conic section. This is a more general statement because five points uniquely determine a conic sections so if $X, Y, Z, W$ and $P$ lie on a circle then this circle is the conic section so $O$ also lies on this circle. In the same way if $X, Y, Z$, $W$ and $O$ are on a circle then it also contains $P$.\n\nLet $E$ be the intersection of the lines $A^{\\prime} B$ and $C D^{\\prime}$. Let $F$ be the intersection of the lines $A^{\\prime} D$ and $B^{\\prime} C$. Finally, let $G$ be the intesection of $X Y$ and $Z W$.\n\nNow we use Pascal's theorem five times:", "metadata": {"resource_path": "EGMO/segmented/en-2022-solutions.jsonl", "problem_match": "# Problem 6.", "solution_match": "\nSolution 3. "}} | |