| {"year": "2009", "tier": "T4", "problem_label": "1", "problem_type": "Geometry", "exam": "HMMT", "problem": "A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.\n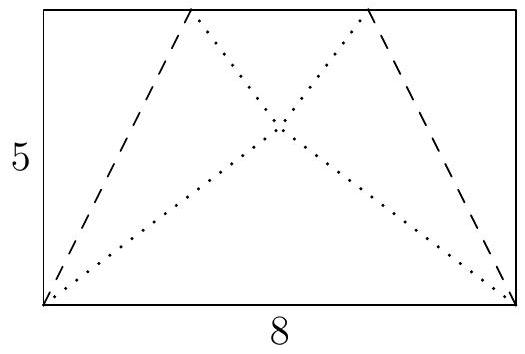", "solution": "$55 / 2$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n1. [3]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "1", "problem_type": "Geometry", "exam": "HMMT", "problem": "A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.\n", "solution": "Drawing the perpendiculars from the point of intersection of the corners to the bases of the trapezoid, we see that we have similar $3-4-5$ right triangles, and we can calculate that the length of the smaller base is 3 . Thus the area of the trapezoid is $\\frac{8+3}{2} \\cdot 5=55 / 2$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n1. [3]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "2", "problem_type": "Geometry", "exam": "HMMT", "problem": "The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?", "solution": "$2 \\sqrt{3} / 3$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n2. [3]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "2", "problem_type": "Geometry", "exam": "HMMT", "problem": "The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?", "solution": "The major diagonal has a length of $\\sqrt{3}$. The volume of the pyramid is $1 / 6$, and so its height $h$ satisfies $\\frac{1}{3} \\cdot h \\cdot \\frac{\\sqrt{3}}{4}(\\sqrt{2})^{2}=1 / 6$ since the freshly cut face is an equilateral triangle of side length $\\sqrt{2}$. Thus $h=\\sqrt{3} / 3$, and the answer follows.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n2. [3]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "3", "problem_type": "Geometry", "exam": "HMMT", "problem": "Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?", "solution": "$3 / 2$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n3. [4]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "3", "problem_type": "Geometry", "exam": "HMMT", "problem": "Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?", "solution": "The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n3. [4]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "4", "problem_type": "Geometry", "exam": "HMMT", "problem": "A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\\angle B=$ $\\angle D=90^{\\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\\prime} C^{\\prime} D^{\\prime}$ that is similar to $A B C D$ and whose incircle is $\\omega$. Let $N^{\\prime}$ be the point of tangency of $B^{\\prime} C^{\\prime}$ to $\\omega$. If $M N^{\\prime} \\| A C$, then what is the ratio of $A B: B C$ ?", "solution": "$\\frac{1+\\sqrt{5}}{2}$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n4. [4]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "4", "problem_type": "Geometry", "exam": "HMMT", "problem": "A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\\angle B=$ $\\angle D=90^{\\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\\prime} C^{\\prime} D^{\\prime}$ that is similar to $A B C D$ and whose incircle is $\\omega$. Let $N^{\\prime}$ be the point of tangency of $B^{\\prime} C^{\\prime}$ to $\\omega$. If $M N^{\\prime} \\| A C$, then what is the ratio of $A B: B C$ ?", "solution": "Let's focus on the right triangle $A B C$ and the semicircle inscribed in it since the situation is symmetric about $A C$. First we find the radius $a$ of circle $O$. Let $A B=x$ and $B C=y$. Drawing the radii $O M$ and $O N$, we see that $A M=x-a$ and $\\triangle A M O \\sim \\triangle A B C$. In other words,\n\n$$\n\\begin{aligned}\n\\frac{A M}{M O} & =\\frac{A B}{B C} \\\\\n\\frac{x-a}{a} & =\\frac{x}{y} \\\\\na & =\\frac{x y}{x+y} .\n\\end{aligned}\n$$\n\nNow we notice that the situation is homothetic about $A$. In particular,\n\n$$\n\\triangle A M O \\sim \\triangle O N C \\sim \\triangle C N^{\\prime} C^{\\prime}\n$$\n\nAlso, $C B$ and $C N^{\\prime}$ are both radii of circle $C$. Thus, when $M N^{\\prime} \\| A C^{\\prime}$, we have\n\n$$\n\\begin{aligned}\nA M & =C N^{\\prime}=C B \\\\\nx-a & =y \\\\\na=\\frac{x y}{x+y} & =x-y \\\\\nx^{2}-x y-y^{2} & =0 \\\\\nx & =\\frac{y}{2} \\pm \\sqrt{\\frac{y^{2}}{4}+y^{2}} \\\\\n\\frac{A B}{B C}=\\frac{x}{y} & =\\frac{1+\\sqrt{5}}{2} .\n\\end{aligned}\n$$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n4. [4]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "5", "problem_type": "Geometry", "exam": "HMMT", "problem": "Circle $B$ has radius $6 \\sqrt{7}$. Circle $A$, centered at point $C$, has radius $\\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.", "solution": "$168 \\pi$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n5. [4]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "5", "problem_type": "Geometry", "exam": "HMMT", "problem": "Circle $B$ has radius $6 \\sqrt{7}$. Circle $A$, centered at point $C$, has radius $\\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.", "solution": "The conditions imply that there exists a triangle such that $B$ is the circumcircle and $A$ is the incircle for the position of $A$. The distance between the circumcenter and incenter is given by $\\sqrt{(R-2 r) R}$, where $R, r$ are the circumradius and inradius, respectively. Thus the locus of $C$ is a circle concentric to $B$ with radius $2 \\sqrt{42}$. The conclusion follows.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n5. [4]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "6", "problem_type": "Geometry", "exam": "HMMT", "problem": "Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.", "solution": "$1+5 \\sqrt{2}+\\sqrt{65}$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n6. [4]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "6", "problem_type": "Geometry", "exam": "HMMT", "problem": "Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.", "solution": "Let $a$ denote the area of the triangle, $r$ the inradius, and $p$ the perimeter. Then $a=r p / 2$, so $r=2 a / p>2 a / 17$. Notice that $a=h / 2$ where $h$ is the height of the triangle from $C$ to $A B$, and $h$ is an integer since the vertices are lattice points. Thus we first guess that the inradius is minimized when $h=1$ and the area is $1 / 2$. In this case, we can now assume WLOG that $A=(0,0), B=(1,0)$, and $C=(n+1,1)$ for some nonnegative integer $n$. The perimeter of $A B C$ is $\\sqrt{n^{2}+2 n+2}+\\sqrt{n^{2}+1}+1$. Since $n=8$ yields a perimeter greater than 17 , the required triangle has $n=7$ and inradius $r=1 / p=$ $\\frac{1}{1+5 \\sqrt{2}+\\sqrt{65}}$ which yields the answer of $1 / r=1+5 \\sqrt{2}+\\sqrt{65}$. We can now verify that this is indeed\nminimal over all $h$ by noting that its perimeter is greater than $17 / 2$, which is the upper bound in the case $h \\geq 2$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n6. [4]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "7", "problem_type": "Geometry", "exam": "HMMT", "problem": "In $\\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.", "solution": "$\\frac{6 \\sqrt{37}}{5}, \\frac{21}{205} \\sqrt{7585}$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n7. [5]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "7", "problem_type": "Geometry", "exam": "HMMT", "problem": "In $\\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.", "solution": "There are two possibilities for the triangle $A B C$ based on whether $E$ is between $B$ and $C$ or not. We first consider the former case.\nWe find from the area and the Pythagorean theorem that $A E=12, A B=13$, and $A C=15$. We can then use Stewart's theorem to obtain $A D=2 \\sqrt{37}$.\nSince the area of $\\triangle A D C$ is half that of $A B C$, we have $\\frac{1}{2} A C \\cdot D F=42$, so $D F=14 / 5$. Also, $D C=14 / 2=7$ so $E D=9-7=2$.\nNotice that $A E D F$ is a cyclic quadrilateral. By Ptolemy's theorem, we have $E F \\cdot 2 \\sqrt{37}=(28 / 5) \\cdot 12+$ $2 \\cdot(54 / 5)$. Thus $E F=\\frac{6 \\sqrt{37}}{5}$ as desired.\nThe latter case is similar.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n7. [5]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "8", "problem_type": "Geometry", "exam": "HMMT", "problem": "Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.", "solution": "208", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n8. [7]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "8", "problem_type": "Geometry", "exam": "HMMT", "problem": "Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.", "solution": "Note that $\\angle A B C$ is right since\n\n$$\nB C^{2}=160^{2}=50 \\cdot 512=(A C-A B) \\cdot(A C+A B)=A C^{2}-A B^{2}\n$$\n\nConstruct point $B^{\\prime}$ such that $A B C B^{\\prime}$ is a rectangle, and construct $D^{\\prime}$ on segment $B^{\\prime} C$ such that $A D=A D^{\\prime}$. Then\n\n$$\nB^{\\prime} D^{\\prime 2}=A D^{\\prime 2}-A B^{\\prime 2}=A D^{2}-B C^{2}=(A D-B C)(A D+B C)=18 \\cdot 338=78^{2}\n$$\n\nIt follows that $C D^{\\prime}=B^{\\prime} C-B^{\\prime} D^{\\prime}=153=C D$; thus, points $D$ and $D^{\\prime}$ coincide, and $A B \\| C D$. Let $M$ denote the midpoint of segment $A D$, and denote the orthogonal projections $M$ to lines $A B$ and $B C$ by $P$ and $Q$ respectively. Then $Q$ is the midpoint of $B C$ and $A P=39$, so that $P B=A B-A P=192$ and\n\n$$\nB M=P Q=\\sqrt{80^{2}+192^{2}}=16 \\sqrt{5^{2}+12^{2}}=208\n$$", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n8. [7]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "9", "problem_type": "Geometry", "exam": "HMMT", "problem": "Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\\angle A B C$ and $\\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.", "solution": "14", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n9. [7]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "9", "problem_type": "Geometry", "exam": "HMMT", "problem": "Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\\angle A B C$ and $\\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.", "solution": "As the incenter of triangle $A B C$, point $P$ has many properties. Extend $A P$ past $P$ to its intersection with the circumcircle of triangle $A B C$, and call this intersection $M$. Now observe that\n\n$$\n\\angle P B M=\\angle P B C+\\angle C B M=\\angle P B C+\\angle C A M=\\beta+\\alpha=90-\\gamma\n$$\n\nwhere $\\alpha, \\beta$, and $\\gamma$ are the half-angles of triangle $A B C$. Since\n\n$$\n\\angle B M P=\\angle B M A=\\angle B C A=2 \\gamma\n$$\n\nit follows that $B M=M P=C M$. Let $Q$ denote the intersection of $A M$ and $B C$, and observe that $\\triangle A Q B \\sim \\triangle C Q M$ and $\\triangle A Q C \\sim \\triangle B Q M$; some easy algebra gives\n\n$$\nA M / B C=(A B \\cdot A C+B M \\cdot C M) /(A C \\cdot C M+A B \\cdot B M)\n$$\n\nWriting $(a, b, c, d, x)=(B C, A C, A B, M P, A P)$, this is $(x+d) / a=\\left(b c+d^{2}\\right) /((b+c) d)$. Ptolemy's theorem applied to $A B C D$ gives $a(d+x)=d(b+c)$. Multiplying the two gives $(d+x)^{2}=b c+d^{2}$. We easily solve for $d=\\left(b c-x^{2}\\right) /(2 x)=8$ and $a=d(b+c) /(d+x)=14$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n9. [7]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "10", "problem_type": "Geometry", "exam": "HMMT", "problem": "Points $A$ and $B$ lie on circle $\\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\\ell$ passes through $P$ and is tangent to $\\omega$. The tangents to $\\omega$ at points $A$ and $B$ intersect $\\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.", "solution": "9", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n10. [8]", "solution_match": "\nAnswer: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "10", "problem_type": "Geometry", "exam": "HMMT", "problem": "Points $A$ and $B$ lie on circle $\\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\\ell$ passes through $P$ and is tangent to $\\omega$. The tangents to $\\omega$ at points $A$ and $B$ intersect $\\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.", "solution": "Say that $\\ell$ be tangent to $\\omega$ at point $T$. Observing equal tangents, write\n\n$$\nC D=C T+D T=B C+A D=5 .\n$$\n\nLet the tangents to $\\omega$ at $A$ and $B$ intersect each other at $Q$. Working from Menelaus applied to triangle $C D Q$ and line $A B$ gives\n\n$$\n\\begin{aligned}\n-1 & =\\frac{D A}{A Q} \\cdot \\frac{Q B}{B C} \\cdot \\frac{C P}{P D} \\\\\n& =\\frac{D A}{B C} \\cdot \\frac{C P}{P C+C D} \\\\\n& =\\frac{3}{2} \\cdot \\frac{C P}{P C+5},\n\\end{aligned}\n$$\n\nfrom which $P C=10$. By power of a point, $P T^{2}=A P \\cdot B P$, or $12^{2}=B P \\cdot(B P+7)$, from which $B P=9$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl", "problem_match": "\n10. [8]", "solution_match": "\nSolution: "}} | |