| {"year": "2009", "tier": "T4", "problem_label": "1", "problem_type": null, "exam": "HMMT", "problem": "What are the chromatic numbers of each of the three graphs shown below? Draw a coloring having the minimum number of colors for each. Label the vertices with symbols to indicate the color of each vertex. (For example, you may mark a vertex \"R\" if you wish to indicate that it is colored red.)\n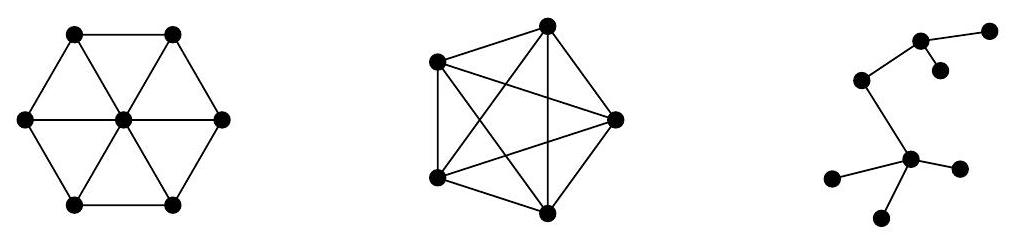", "solution": "The chromatic numbers of the three graphs are 3,5 , and 2 , respectively.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n1. [6]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "2", "problem_type": null, "exam": "HMMT", "problem": "In a connected graph, it is possible to reach any vertex from any other vertex by following the edges. A tree is a connected graph with $n$ vertices and $n-1$ edges for some positive integer $n$. Suppose $n \\geq 2$. What is the chromatic number of a tree having $n$ vertices? Prove your answer.", "solution": "The chromatic number of any tree is 2 . We show this by induction on the size of the tree. A tree with 2 nodes can clearly be 2 -colored. Now, suppose a tree of size $n-1$ can be colored in 2 colors. Given a tree of size $n$, choose any leaf (node with only one edge coming out of it), say $l$, of the tree, and color it red. The node it is adjacent to, say $x$, must be colored a different color, say blue. Using the inductive hypothesis, we can 2-color the tree formed by removing $l$, and we can choose the color of $x$ to be blue and the other color to be red. Thus the entire tree on $n$ vertices can be two-colored, completing the induction.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n2. [6]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "3", "problem_type": null, "exam": "HMMT", "problem": "Let $n \\geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.\nFor a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.", "solution": "We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3 . Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an $n-1$-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n3. [8]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "4", "problem_type": null, "exam": "HMMT", "problem": "Let $G$ be a finite graph in which every vertex has degree less than or equal to $k$. Prove that the chromatic number of $G$ is less than or equal to $k+1$.", "solution": "Using a greedy algorithm we find a good coloring with $k+1$ colors. Order the vertices and color them one by one - since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n4. [10]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "5", "problem_type": null, "exam": "HMMT", "problem": "A $k$-clique of a graph is a set of $k$ vertices such that all pairs of vertices in the clique are adjacent. The clique number of a graph is the size of the largest clique in the graph. Does there exist a graph which has a clique number smaller than its chromatic number?", "solution": "Consider a graph with 5 vertices arranged in a circle, with each vertex connected to its two neighbors. If only two colors are used, it is impossible to alternate colors to avoid using the same color on two adjacent vertices, so the chromatic number is 3 . Its clique number is 2 , so we have found such a graph.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n5. [10]", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "6", "problem_type": null, "exam": "HMMT", "problem": "(a) [5] If a single vertex (and all its incident edges) is removed from a finite graph, show that the graph's chromatic number cannot decrease by more than 1.", "solution": "Suppose the chromatic number of the graph was $C$, and removing a single vertex resulted in a graph with chromatic number at most $C-2$. Then we can color the remaining graph with at most $C-2$ colors. Replacing the vertex and its edges, we can then choose any color not already used to form a coloring of the original graph using at most $C-1$ colors, contradicting the fact that $C$ is the chromatic number of the graph.\n(b) [15] Show that, for any $n>2$, there are infinitely many graphs with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n6. ", "solution_match": "\nSolution: "}} | |
| {"year": "2009", "tier": "T4", "problem_label": "6", "problem_type": null, "exam": "HMMT", "problem": "(a) [5] If a single vertex (and all its incident edges) is removed from a finite graph, show that the graph's chromatic number cannot decrease by more than 1.", "solution": "Let $k>0$ be an odd number, and let $G$ be a graph with $k$ vertices arranged in a circle, with each vertex connected to its two neighbors. If $n=3$, these graphs can be arbitrarily large, and are the graphs we need. If $n>3$, let $H$ be a complete graph on $n-3$ vertices, and let $J$ be the graph created by adding an edge from every vertex in $G$ to every vertex in $H$. Then $n-3$ colors are needed to color $H$ and another 3 are needed to color $G$, so $n$ colors is both necessary and sufficient for a good coloring of $J$. Now, say a vertex is removed from $J$. There are two cases:\nIf the vertex was removed from $G$, then the remaining vertices in $G$ can be colored with 2 colors, because the cycle has been broken. A set of $n-3$ different colors can be used to color $H$, so only $n-1$ colors are needed to color the reduced graph. On the other hand, if the vertex was removed from $H$, then $n-4$ colors are used to color $H$ and 3 used to color $G$. So removing any vertex decreases the chromatic number of $J$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl", "problem_match": "\n6. ", "solution_match": "\nSolution: "}} | |