| {"year": "2010", "tier": "T4", "problem_label": "1", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "Let $S=\\{1,2,3,4,5,6,7,8,9,10\\}$. How many (potentially empty) subsets $T$ of $S$ are there such that, for all $x$, if $x$ is in $T$ and $2 x$ is in $S$ then $2 x$ is also in $T$ ?", "solution": "180 We partition the elements of $S$ into the following subsets: $\\{1,2,4,8\\},\\{3,6\\},\\{5,10\\}$, $\\{7\\},\\{9\\}$. Consider the first subset, $\\{1,2,4,8\\}$. Say 2 is an element of $T$. Because $2 \\cdot 2=4$ is in $S, 4$ must also be in $T$. Furthermore, since $4 \\cdot 2=8$ is in $S, 8$ must also be in $T$. So if $T$ contains 2 , it must also contain 4 and 8 . Similarly, if $T$ contains 1 , it must also contain 2,4 , and 8 . So $T$ can contain the following subsets of the subset $\\{1,2,4,8\\}$ : the empty set, $\\{8\\},\\{4,8\\},\\{2,4,8\\}$, or $\\{1,2,4,8\\}$. This gives 5 possibilities for the first subset. In general, we see that if $T$ contains an element $q$ of one of these subsets, it must also contain the elements in that subset that are larger than $q$, because we created the subsets for this to be true. So there are 3 possibilities for $\\{3,6\\}, 3$ for $\\{5,10\\}, 2$ for $\\{7\\}$, and 2 for $\\{9\\}$. This gives a total of $5 \\cdot 3 \\cdot 3 \\cdot 2 \\cdot 2=180$ possible subsets $T$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n1. [2]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "2", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0! and 1! to be distinct.", "solution": "39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain 3 !, 4 !, 5 !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \\cdot 2 \\cdot 2 \\cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n2. [3]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "3", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "How many ways are there to choose 2010 functions $f_{1}, \\ldots, f_{2010}$ from $\\{0,1\\}$ to $\\{0,1\\}$ such that $f_{2010} \\circ f_{2009} \\circ \\cdots \\circ f_{1}$ is constant? Note: a function $g$ is constant if $g(a)=g(b)$ for all $a, b$ in the domain of $g$.", "solution": "$4^{2010}-2^{2010}$ If all 2010 functions are bijective ${ }^{1}$, then the composition $f_{2010} \\circ f_{2009} \\circ \\cdots \\circ f_{1}$ will be bijective also, and therefore not constant. If, however, one of $f_{1}, \\ldots, f_{2010}$ is not bijective, say $f_{k}$, then $f_{k}(0)=f_{k}(1)=q$, so $f_{2010} \\circ f_{2009} \\circ \\cdots \\circ f_{k+1} \\circ f_{k} \\circ \\cdots f_{1}(0)=f_{2010} \\circ f_{2009} \\circ \\cdots \\circ f_{k+1}(q)=$ $f_{2010} \\circ f_{2009} \\circ \\cdots \\circ f_{k+1} \\circ f_{k} \\circ \\cdots f_{1}(1)$. So the composition will be constant unless all $f_{i}$ are bijective. Since there are 4 possible functions ${ }^{2}$ from $\\{0,1\\}$ to $\\{0,1\\}$ and 2 of them are bijective, we subtract the cases where all the functions are bijective from the total to get $4^{2010}-2^{2010}$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n3. [4]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "4", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).\n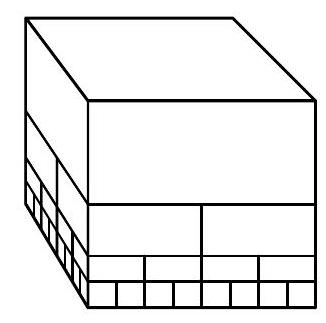", "solution": "3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \\cdot 4 \\cdot 7 \\cdot 10 \\cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \\cdot 4 \\cdot 4 \\cdot 4 \\cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \\cdot 4 \\cdot 7 \\cdot 10 \\cdot 13-1 \\cdot 4 \\cdot 4 \\cdot 4 \\cdot 4=3384$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n4. [4]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "5", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "John needs to pay 2010 dollars for his dinner. He has an unlimited supply of 2, 5, and 10 dollar notes. In how many ways can he pay?", "solution": "20503\nLet the number of 2,5 , and 10 dollar notes John can use be $x, y$, and $z$ respectively. We wish to find the number of nonnegative integer solutions to $2 x+5 y+10 z=2010$. Consider this equation $\\bmod 2$. Because $2 x, 10 z$, and 2010 are even, $5 y$ must also be even, so $y$ must be even. Now consider the equation mod 5 . Because $5 y, 10 z$, and 2010 are divisible by $5,2 x$ must also be divisible by 5 , so $x$ must be divisible by 5 . So both $2 x$ and $5 y$ are divisible by 10 . So the equation is equivalent to $10 x^{\\prime}+10 y^{\\prime}+10 z=2010$, or $x^{\\prime}+y^{\\prime}+z=201$, with $x^{\\prime}, y^{\\prime}$, and $z$ nonnegative integers. There is a well-known bijection between solutions of this equation and picking 2 of 203 balls in a row on the table (explained in further detail below), so there are $\\binom{203}{2}=20503$ ways.\nThe bijection between solutions of $x^{\\prime}+y^{\\prime}+z=201$ and arrangements of 203 balls in a row is as follows. Given a solution of the equation, we put $x^{\\prime}$ white balls in a row, then a black ball, then $y^{\\prime}$ white balls, then a black ball, then $z$ white balls. This is like having 203 balls in a row on a table and picking two of them to be black. To go from an arrangement of balls to a solution of the equation, we just read off $x^{\\prime}, y^{\\prime}$, and $z$ from the number of white balls in a row. There are $\\binom{203}{2}$ ways to choose 2 of 203 balls to be black, so there are $\\binom{203}{2}$ solutions to $x^{\\prime}+y^{\\prime}+z=201$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n5. [5]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "6", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "An ant starts out at $(0,0)$. Each second, if it is currently at the square $(x, y)$, it can move to $(x-1, y-1),(x-1, y+1),(x+1, y-1)$, or $(x+1, y+1)$. In how many ways can it end up at $(2010,2010)$ after 4020 seconds?", "solution": "$\\binom{4020}{1005}^{2}$ Note that each of the coordinates either increases or decreases the $x$ and $y$ coordinates by 1. In order to reach 2010 after 4020 steps, each of the coordinates must be increased 3015 times and decreased 1005 times. A permutation of 3015 plusses and 1005 minuses for each of $x$ and $y$ uniquely corresponds to a path the ant could take to $(2010,2010)$, because we can take ordered pairs from the two lists and match them up to a valid step the ant can take. So the number of ways the ant can end up at $(2010,2010)$ after 4020 seconds is equal to the number of ways to arrange plusses and minuses for both $x$ and $y$, or $\\left(\\binom{4020}{1005}\\right)^{2}$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n6. [5]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "7", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "For each integer $x$ with $1 \\leq x \\leq 10$, a point is randomly placed at either $(x, 1)$ or $(x,-1)$ with equal probability. What is the expected area of the convex hull of these points? Note: the convex hull of a finite set is the smallest convex polygon containing it.", "solution": "$\\frac{1793}{\\frac{1728}{128}}$ Let $n=10$. Given a random variable $X$, let $\\mathbb{E}(X)$ denote its expected value. If all points are collinear, then the convex hull has area zero. This happens with probability $\\frac{2}{2^{n}}$ (either all points are at $y=1$ or all points are at $y=-1$ ). Otherwise, the points form a trapezoid with height 2 (the trapezoid is possibly degenerate, but this won't matter for our calculation). Let $x_{1, l}$ be the $x$-coordinate of the left-most point at $y=1$ and $x_{1, r}$ be the $x$-coordinate of the right-most point at $y=1$. Define $x_{-1, l}$ and $x_{-1, r}$ similarly for $y=-1$. Then the area of the trapezoid is\n\n$$\n2 \\cdot \\frac{\\left(x_{1, r}-x_{1, l}\\right)+\\left(x_{-1, r}-x_{-1, l}\\right)}{2}=x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l} .\n$$\n\nThe expected area of the convex hull (assuming the points are not all collinear) is then, by linearity of expectation,\n\n$$\n\\mathbb{E}\\left(x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l}\\right)=\\mathbb{E}\\left(x_{1, r}\\right)+\\mathbb{E}\\left(x_{-1, r}\\right)-\\mathbb{E}\\left(x_{1, l}\\right)-\\mathbb{E}\\left(x_{-1, l}\\right) .\n$$\n\nWe need only compute the expected values given in the above equation. Note that $x_{1, r}$ is equal to $k$ with probability $\\frac{2^{k-1}}{2^{n}-2}$, except that it is equal to $n$ with probability $\\frac{2^{n-1}-1}{2^{n}-2}$ (the denominator is $2^{n}-2$ instead of $2^{n}$ because we need to exclude the case where all points are collinear). Therefore, the expected value of $x_{1, r}$ is equal to\n\n$$\n\\begin{aligned}\n& \\frac{1}{2^{n}-2}\\left(\\left(\\sum_{k=1}^{n} k \\cdot 2^{k-1}\\right)-n \\cdot 1\\right) \\\\\n& \\quad=\\frac{1}{2^{n}-2}\\left(\\left(1+2+\\cdots+2^{n-1}\\right)+\\left(2+4+\\cdots+2^{n-1}\\right)+\\cdots+2^{n-1}-n\\right) \\\\\n& =\\frac{1}{2^{n}-2}\\left(\\left(2^{n}-1\\right)+\\left(2^{n}-2\\right)+\\cdots+\\left(2^{n}-2^{n-1}\\right)-n\\right) \\\\\n& =\\frac{1}{2^{n}-2}\\left(n \\cdot 2^{n}-\\left(2^{n}-1\\right)-n\\right) \\\\\n& \\quad=(n-1) \\frac{2^{n}-1}{2^{n}-2}\n\\end{aligned}\n$$\n\nSimilarly, the expected value of $x_{-1, r}$ is also $(n-1) \\frac{2^{n}-1}{2^{n}-2}$. By symmetry, the expected value of both $x_{1, l}$ and $x_{-1, l}$ is $n+1-(n-1) \\frac{\\frac{2}{n}^{n}-1}{2^{n}-2}$. This says that if the points are not all collinear then the expected area is $2 \\cdot\\left((n-1) \\frac{2^{n}-1}{2^{n-1}-1}-(n+1)\\right)$. So, the expected area is\n\n$$\n\\begin{aligned}\n\\frac{2}{2^{n}} \\cdot 0+(1- & \\left.\\frac{2}{2^{n}}\\right) \\cdot 2 \\cdot\\left((n-1) \\frac{2^{n}-1}{2^{n-1}-1}-(n+1)\\right) \\\\\n& =2 \\cdot \\frac{2^{n-1}-1}{2^{n-1}} \\cdot\\left((n-1) \\frac{2^{n}-1}{2^{n-1}-1}-(n+1)\\right) \\\\\n& =2 \\cdot \\frac{(n-1)\\left(2^{n}-1\\right)-(n+1)\\left(2^{n-1}-1\\right)}{2^{n-1}} \\\\\n& =2 \\cdot \\frac{((2 n-2)-(n+1)) 2^{n-1}+2}{2^{n-1}} \\\\\n& =2 n-6+\\frac{1}{2^{n-3}}\n\\end{aligned}\n$$\n\nPlugging in $n=10$, we get $14+\\frac{1}{128}=\\frac{1793}{128}$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n7. [6]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "8", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "How many functions $f$ from $\\{-1005, \\ldots, 1005\\}$ to $\\{-2010, \\ldots, 2010\\}$ are there such that the following two conditions are satisfied?\n\n- If $a<b$ then $f(a)<f(b)$.\n- There is no $n$ in $\\{-1005, \\ldots, 1005\\}$ such that $|f(n)|=|n|$.", "solution": "$\\cdots$ Note: the intended answer was $\\binom{4019}{2011}$, but the original answer was incorrect. The correct answer is:\n1173346782666677300072441773814388000553179587006710786401225043842699552460942166630860 5302966355504513409792805200762540756742811158611534813828022157596601875355477425764387 2333935841666957750009216404095352456877594554817419353494267665830087436353494075828446 0070506487793628698617665091500712606599653369601270652785265395252421526230453391663029 1476263072382369363170971857101590310272130771639046414860423440232291348986940615141526 0247281998288175423628757177754777309519630334406956881890655029018130367627043067425502 2334151384481231298380228052789795136259575164777156839054346649261636296328387580363485 2904329986459861362633348204891967272842242778625137520975558407856496002297523759366027\n\n1506637984075036473724713869804364399766664507880042495122618597629613572449327653716600 6715747717529280910646607622693561789482959920478796128008380531607300324374576791477561 5881495035032334387221203759898494171708240222856256961757026746724252966598328065735933 6668742613422094179386207330487537984173936781232801614775355365060827617078032786368164 8860839124954588222610166915992867657815394480973063139752195206598739798365623873142903 28539769699667459275254643229234106717245366005816917271187760792\n\nThis obviously cannot be computed by hand, but there is a polynomial-time dynamic programming algorithm that will compute it.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n8. [6]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "9", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "Rosencrantz and Guildenstern are playing a game where they repeatedly flip coins. Rosencrantz wins if 1 heads followed by 2009 tails appears. Guildenstern wins if 2010 heads come in a row. They will flip coins until someone wins. What is the probability that Rosencrantz wins?", "solution": "$\\frac{2^{2009}-1}{3 \\cdot 2^{2008}-1}$ We can assume the first throw is heads (because neither player can win starting from a string of only tails). Let $x$ be the probability that Rosencrantz wins. Let $y$ be the probability that Rosencrantz wins after HT.\n\nWhenever there is a string of less than 2009 tails followed by a heads, the heads basically means the two are starting from the beginning, where Rosencrantz has probability $x$ of winning.\nWe also know that $x=y\\left(1-\\frac{1}{2^{2009}}\\right)$. This is because from the initial heads there is a $\\left(1-\\frac{1}{2^{2009}}\\right)$ chance Rosencrantz doesn't lose, and in this case the last two flips are HT, in which case Rosencrantz has probability $y$ of winning.\nIf the first two throws are HT, there is a $\\frac{1}{2^{2008}}$ chance Rosencrantz wins; otherwise, there is eventually a heads, and so we are back in the case of starting from a heads, which corresponds to $x$. Therefore, $y=\\frac{1}{2^{2008}}+x\\left(1-\\frac{1}{2^{2008}}\\right)$. Putting this together with the previous equation, we get:\n\n$$\n\\begin{aligned}\nx & =\\left(\\frac{1}{2^{2008}}+x\\left(1-\\frac{1}{2^{2008}}\\right)\\right)\\left(1-\\frac{1}{2^{2009}}\\right) \\\\\n\\Longrightarrow \\quad x & =\\left(\\frac{1+2^{2008} x-x}{2^{2008}}\\right)\\left(\\frac{2^{2009}-1}{\\left.2^{2009}\\right)}\\right. \\\\\n\\Longrightarrow \\quad 2^{4017} x & =x\\left(2^{4017}-2^{2009}-2^{2008}+1\\right)+2^{2009}-1 \\\\\n\\Longrightarrow \\quad x & =\\frac{2^{2009}-1}{2^{2009}+2^{2008}-1},\n\\end{aligned}\n$$\n\nso the answer is $\\frac{2^{2009}-1}{2^{2009}+2^{2008}-1}=\\frac{2^{2009}-1}{3 \\cdot 2^{2008}-1}$.", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n9. [7]", "solution_match": "\nAnswer: "}} | |
| {"year": "2010", "tier": "T4", "problem_label": "10", "problem_type": "Combinatorics", "exam": "HMMT", "problem": "In a $16 \\times 16$ table of integers, each row and column contains at most 4 distinct integers. What is the maximum number of distinct integers that there can be in the whole table?", "solution": "49 First, we show that 50 is too big. Assume for sake of contradiction that a labeling with at least 50 distinct integers exists. By the Pigeonhole Principle, there must be at least one row, say the first row, with at least 4 distinct integers in it; in this case, that is exactly 4 , since that is the maximum number of distinct integers in one row. Then, in the remaining 15 rows there must be at least 46 distinct integers (these 46 will also be distinct from the 4 in the first row). Using Pigeonhole again, there will be another row, say the second row, with 4 distinct integers in it. Call the set of integers in the first and second rows $S$. Because the 4 distinct integers in the second row are distinct from the 4 in the first row, there are 8 distinct values in the first two rows, so $|S|=8$. Now consider the subcolumns containing the cells in rows 3 to 16 . In each subcolumn, there are at most 2 values not in $S$, because there are already two distinct values in that column from the cells in the first two rows. So, the maximum number of distinct values in the table is $16 \\cdot 2+8=40$, a contradiction. So a valid labeling must have fewer than 50 distinct integers. Below, we show by example that 49 is attainable.\n\n| 1 | 17 | 33 | - | - | - | - | - | - | - | - | - | - | - | - | - |\n| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |\n| - | 2 | 18 | 34 | - | - | - | - | - | - | - | - | - | - | - | - |\n| - | - | 3 | 19 | 35 | - | - | - | - | - | - | - | - | - | - | - |\n| - | - | - | 4 | 20 | 36 | - | - | - | - | - | - | - | - | - | - |\n| - | - | - | - | 5 | 21 | 37 | - | - | - | - | - | - | - | - | - |\n| - | - | - | - | - | 6 | 22 | 38 | - | - | - | - | - | - | - | - |\n| - | - | - | - | - | - | 7 | 23 | 39 | - | - | - | - | - | - | - |\n| - | - | - | - | - | - | - | 8 | 24 | 40 | - | - | - | - | - | - |\n| - | - | - | - | - | - | - | - | 9 | 25 | 41 | - | - | - | - | - |\n| - | - | - | - | - | - | - | - | - | 10 | 26 | 42 | - | - | - | - |\n| - | - | - | - | - | - | - | - | - | - | 11 | 27 | 43 | - | - | - |\n| - | - | - | - | - | - | - | - | - | - | - | 12 | 28 | 44 | - | - |\n| - | - | - | - | - | - | - | - | - | - | - | - | 13 | 29 | 45 | - |\n| - | - | - | - | - | - | - | - | - | - | - | - | - | 14 | 30 | 46 |\n| 47 | - | - | - | - | - | - | - | - | - | - | - | - | - | 15 | 31 |\n| 32 | 48 | - | - | - | - | - | - | - | - | - | - | - | - | - | 16 |\n\nCells that do not contain a number are colored with color 49 .", "metadata": {"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl", "problem_match": "\n10. [8]", "solution_match": "\nAnswer: "}} | |