| {"year": "2007", "tier": "T0", "problem_label": "A1", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Given a sequence $a_{1}, a_{2}, \\ldots, a_{n}$ of real numbers. For each $i(1 \\leq i \\leq n)$ define $$ d_{i}=\\max \\left\\{a_{j}: 1 \\leq j \\leq i\\right\\}-\\min \\left\\{a_{j}: i \\leq j \\leq n\\right\\} $$ and let $$ d=\\max \\left\\{d_{i}: 1 \\leq i \\leq n\\right\\} $$ (a) Prove that for arbitrary real numbers $x_{1} \\leq x_{2} \\leq \\ldots \\leq x_{n}$, $$ \\max \\left\\{\\left|x_{i}-a_{i}\\right|: 1 \\leq i \\leq n\\right\\} \\geq \\frac{d}{2} $$ (b) Show that there exists a sequence $x_{1} \\leq x_{2} \\leq \\ldots \\leq x_{n}$ of real numbers such that we have equality in (1). (New Zealand)", "solution": "(a) Let $1 \\leq p \\leq q \\leq r \\leq n$ be indices for which $$ d=d_{q}, \\quad a_{p}=\\max \\left\\{a_{j}: 1 \\leq j \\leq q\\right\\}, \\quad a_{r}=\\min \\left\\{a_{j}: q \\leq j \\leq n\\right\\} $$ and thus $d=a_{p}-a_{r}$. (These indices are not necessarily unique.) 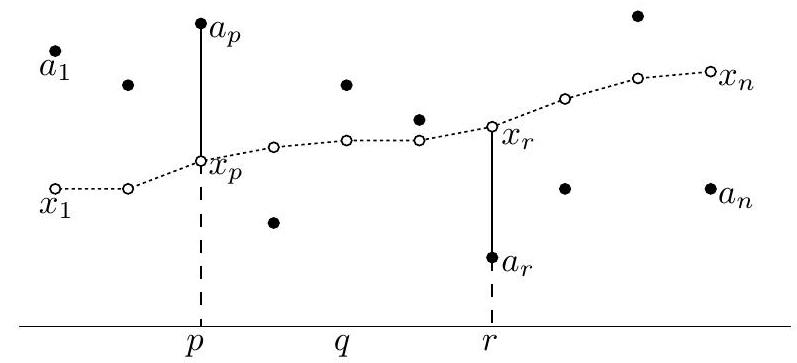 For arbitrary real numbers $x_{1} \\leq x_{2} \\leq \\ldots \\leq x_{n}$, consider just the two quantities $\\left|x_{p}-a_{p}\\right|$ and $\\left|x_{r}-a_{r}\\right|$. Since $$ \\left(a_{p}-x_{p}\\right)+\\left(x_{r}-a_{r}\\right)=\\left(a_{p}-a_{r}\\right)+\\left(x_{r}-x_{p}\\right) \\geq a_{p}-a_{r}=d, $$ we have either $a_{p}-x_{p} \\geq \\frac{d}{2}$ or $x_{r}-a_{r} \\geq \\frac{d}{2}$. Hence, $$ \\max \\left\\{\\left|x_{i}-a_{i}\\right|: 1 \\leq i \\leq n\\right\\} \\geq \\max \\left\\{\\left|x_{p}-a_{p}\\right|,\\left|x_{r}-a_{r}\\right|\\right\\} \\geq \\max \\left\\{a_{p}-x_{p}, x_{r}-a_{r}\\right\\} \\geq \\frac{d}{2} $$ (b) Define the sequence $\\left(x_{k}\\right)$ as $$ x_{1}=a_{1}-\\frac{d}{2}, \\quad x_{k}=\\max \\left\\{x_{k-1}, a_{k}-\\frac{d}{2}\\right\\} \\quad \\text { for } 2 \\leq k \\leq n $$ We show that we have equality in (1) for this sequence. By the definition, sequence $\\left(x_{k}\\right)$ is non-decreasing and $x_{k}-a_{k} \\geq-\\frac{d}{2}$ for all $1 \\leq k \\leq n$. Next we prove that $$ x_{k}-a_{k} \\leq \\frac{d}{2} \\quad \\text { for all } 1 \\leq k \\leq n $$ Consider an arbitrary index $1 \\leq k \\leq n$. Let $\\ell \\leq k$ be the smallest index such that $x_{k}=x_{\\ell}$. We have either $\\ell=1$, or $\\ell \\geq 2$ and $x_{\\ell}>x_{\\ell-1}$. In both cases, $$ x_{k}=x_{\\ell}=a_{\\ell}-\\frac{d}{2} $$ Since $$ a_{\\ell}-a_{k} \\leq \\max \\left\\{a_{j}: 1 \\leq j \\leq k\\right\\}-\\min \\left\\{a_{j}: k \\leq j \\leq n\\right\\}=d_{k} \\leq d $$ equality (3) implies $$ x_{k}-a_{k}=a_{\\ell}-a_{k}-\\frac{d}{2} \\leq d-\\frac{d}{2}=\\frac{d}{2} $$ We obtained that $-\\frac{d}{2} \\leq x_{k}-a_{k} \\leq \\frac{d}{2}$ for all $1 \\leq k \\leq n$, so $$ \\max \\left\\{\\left|x_{i}-a_{i}\\right|: 1 \\leq i \\leq n\\right\\} \\leq \\frac{d}{2} $$ We have equality because $\\left|x_{1}-a_{1}\\right|=\\frac{d}{2}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A1", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Given a sequence $a_{1}, a_{2}, \\ldots, a_{n}$ of real numbers. For each $i(1 \\leq i \\leq n)$ define $$ d_{i}=\\max \\left\\{a_{j}: 1 \\leq j \\leq i\\right\\}-\\min \\left\\{a_{j}: i \\leq j \\leq n\\right\\} $$ and let $$ d=\\max \\left\\{d_{i}: 1 \\leq i \\leq n\\right\\} $$ (a) Prove that for arbitrary real numbers $x_{1} \\leq x_{2} \\leq \\ldots \\leq x_{n}$, $$ \\max \\left\\{\\left|x_{i}-a_{i}\\right|: 1 \\leq i \\leq n\\right\\} \\geq \\frac{d}{2} $$ (b) Show that there exists a sequence $x_{1} \\leq x_{2} \\leq \\ldots \\leq x_{n}$ of real numbers such that we have equality in (1). (New Zealand)", "solution": "We present another construction of a sequence $\\left(x_{i}\\right)$ for part (b). For each $1 \\leq i \\leq n$, let $$ M_{i}=\\max \\left\\{a_{j}: 1 \\leq j \\leq i\\right\\} \\quad \\text { and } \\quad m_{i}=\\min \\left\\{a_{j}: i \\leq j \\leq n\\right\\} $$ For all $1 \\leq i<n$, we have $$ M_{i}=\\max \\left\\{a_{1}, \\ldots, a_{i}\\right\\} \\leq \\max \\left\\{a_{1}, \\ldots, a_{i}, a_{i+1}\\right\\}=M_{i+1} $$ and $$ m_{i}=\\min \\left\\{a_{i}, a_{i+1}, \\ldots, a_{n}\\right\\} \\leq \\min \\left\\{a_{i+1}, \\ldots, a_{n}\\right\\}=m_{i+1} . $$ Therefore sequences $\\left(M_{i}\\right)$ and $\\left(m_{i}\\right)$ are non-decreasing. Moreover, since $a_{i}$ is listed in both definitions, $$ m_{i} \\leq a_{i} \\leq M_{i} $$ To achieve equality in (1), set $$ x_{i}=\\frac{M_{i}+m_{i}}{2} . $$ Since sequences $\\left(M_{i}\\right)$ and $\\left(m_{i}\\right)$ are non-decreasing, this sequence is non-decreasing as well. From $d_{i}=M_{i}-m_{i}$ we obtain that $$ -\\frac{d_{i}}{2}=\\frac{m_{i}-M_{i}}{2}=x_{i}-M_{i} \\leq x_{i}-a_{i} \\leq x_{i}-m_{i}=\\frac{M_{i}-m_{i}}{2}=\\frac{d_{i}}{2} . $$ Therefore $$ \\max \\left\\{\\left|x_{i}-a_{i}\\right|: 1 \\leq i \\leq n\\right\\} \\leq \\max \\left\\{\\frac{d_{i}}{2}: 1 \\leq i \\leq n\\right\\}=\\frac{d}{2} $$ Since the opposite inequality has been proved in part (a), we must have equality.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A2", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Consider those functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ which satisfy the condition $$ f(m+n) \\geq f(m)+f(f(n))-1 $$ for all $m, n \\in \\mathbb{N}$. Find all possible values of $f(2007)$. $(\\mathbb{N}$ denotes the set of all positive integers.) (Bulgaria) Answer. 1, 2, .., 2008.", "solution": "Suppose that a function $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ satisfies (1). For arbitrary positive integers $m>n$, by (1) we have $$ f(m)=f(n+(m-n)) \\geq f(n)+f(f(m-n))-1 \\geq f(n), $$ so $f$ is nondecreasing. Function $f \\equiv 1$ is an obvious solution. To find other solutions, assume that $f \\not \\equiv 1$ and take the smallest $a \\in \\mathbb{N}$ such that $f(a)>1$. Then $f(b) \\geq f(a)>1$ for all integer $b \\geq a$. Suppose that $f(n)>n$ for some $n \\in \\mathbb{N}$. Then we have $$ f(f(n))=f((f(n)-n)+n) \\geq f(f(n)-n)+f(f(n))-1 $$ so $f(f(n)-n) \\leq 1$ and hence $f(n)-n<a$. Then there exists a maximal value of the expression $f(n)-n$; denote this value by $c$, and let $f(k)-k=c \\geq 1$. Applying the monotonicity together with (1), we get $$ \\begin{aligned} 2 k+c \\geq f(2 k)=f(k+k) & \\geq f(k)+f(f(k))-1 \\\\ & \\geq f(k)+f(k)-1=2(k+c)-1=2 k+(2 c-1) \\end{aligned} $$ hence $c \\leq 1$ and $f(n) \\leq n+1$ for all $n \\in \\mathbb{N}$. In particular, $f(2007) \\leq 2008$. Now we present a family of examples showing that all values from 1 to 2008 can be realized. Let $$ f_{j}(n)=\\max \\{1, n+j-2007\\} \\quad \\text { for } j=1,2, \\ldots, 2007 ; \\quad f_{2008}(n)= \\begin{cases}n, & 2007 \\not \\mid n \\\\ n+1, & 2007 \\mid n\\end{cases} $$ We show that these functions satisfy the condition (1) and clearly $f_{j}(2007)=j$. To check the condition (1) for the function $f_{j}(j \\leq 2007)$, note first that $f_{j}$ is nondecreasing and $f_{j}(n) \\leq n$, hence $f_{j}\\left(f_{j}(n)\\right) \\leq f_{j}(n) \\leq n$ for all $n \\in \\mathbb{N}$. Now, if $f_{j}(m)=1$, then the inequality (1) is clear since $f_{j}(m+n) \\geq f_{j}(n) \\geq f_{j}\\left(f_{j}(n)\\right)=f_{j}(m)+f_{j}\\left(f_{j}(n)\\right)-1$. Otherwise, $$ f_{j}(m)+f_{j}\\left(f_{j}(n)\\right)-1 \\leq(m+j-2007)+n=(m+n)+j-2007=f_{j}(m+n) . $$ In the case $j=2008$, clearly $n+1 \\geq f_{2008}(n) \\geq n$ for all $n \\in \\mathbb{N}$; moreover, $n+1 \\geq$ $f_{2008}\\left(f_{2008}(n)\\right)$ as well. Actually, the latter is trivial if $f_{2008}(n)=n$; otherwise, $f_{2008}(n)=n+1$, which implies $2007 \\not n n+1$ and hence $n+1=f_{2008}(n+1)=f_{2008}\\left(f_{2008}(n)\\right)$. So, if $2007 \\mid m+n$, then $$ f_{2008}(m+n)=m+n+1=(m+1)+(n+1)-1 \\geq f_{2008}(m)+f_{2008}\\left(f_{2008}(n)\\right)-1 . $$ Otherwise, $2007 \\not m+n$, hence $2007 \\not m$ or $2007 \\not n$. In the former case we have $f_{2008}(m)=m$, while in the latter one $f_{2008}\\left(f_{2008}(n)\\right)=f_{2008}(n)=n$, providing $$ f_{2008}(m)+f_{2008}\\left(f_{2008}(n)\\right)-1 \\leq(m+n+1)-1=f_{2008}(m+n) . $$ Comment. The examples above are not unique. The values $1,2, \\ldots, 2008$ can be realized in several ways. Here we present other two constructions for $j \\leq 2007$, without proof: $$ g_{j}(n)=\\left\\{\\begin{array}{ll} 1, & n<2007, \\\\ j, & n=2007, \\\\ n, & n>2007 ; \\end{array} \\quad h_{j}(n)=\\max \\left\\{1,\\left\\lfloor\\frac{j n}{2007}\\right\\rfloor\\right\\}\\right. $$ Also the example for $j=2008$ can be generalized. In particular, choosing a divisor $d>1$ of 2007 , one can set $$ f_{2008, d}(n)= \\begin{cases}n, & d \\nless\\{n \\\\ n+1, & d \\mid n\\end{cases} $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A3", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $n$ be a positive integer, and let $x$ and $y$ be positive real numbers such that $x^{n}+y^{n}=1$. Prove that $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right)<\\frac{1}{(1-x)(1-y)} $$ (Estonia)", "solution": "For each real $t \\in(0,1)$, $$ \\frac{1+t^{2}}{1+t^{4}}=\\frac{1}{t}-\\frac{(1-t)\\left(1-t^{3}\\right)}{t\\left(1+t^{4}\\right)}<\\frac{1}{t} $$ Substituting $t=x^{k}$ and $t=y^{k}$, $$ 0<\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}<\\sum_{k=1}^{n} \\frac{1}{x^{k}}=\\frac{1-x^{n}}{x^{n}(1-x)} \\quad \\text { and } \\quad 0<\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}<\\sum_{k=1}^{n} \\frac{1}{y^{k}}=\\frac{1-y^{n}}{y^{n}(1-y)} $$ Since $1-y^{n}=x^{n}$ and $1-x^{n}=y^{n}$, $$ \\frac{1-x^{n}}{x^{n}(1-x)}=\\frac{y^{n}}{x^{n}(1-x)}, \\quad \\frac{1-y^{n}}{y^{n}(1-y)}=\\frac{x^{n}}{y^{n}(1-y)} $$ and therefore $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right)<\\frac{y^{n}}{x^{n}(1-x)} \\cdot \\frac{x^{n}}{y^{n}(1-y)}=\\frac{1}{(1-x)(1-y)} . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A3", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $n$ be a positive integer, and let $x$ and $y$ be positive real numbers such that $x^{n}+y^{n}=1$. Prove that $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right)<\\frac{1}{(1-x)(1-y)} $$ (Estonia)", "solution": "We prove $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right)<\\frac{\\left(\\frac{1+\\sqrt{2}}{2} \\ln 2\\right)^{2}}{(1-x)(1-y)}<\\frac{0.7001}{(1-x)(1-y)} $$ The idea is to estimate each term on the left-hand side with the same constant. To find the upper bound for the expression $\\frac{1+x^{2 k}}{1+x^{4 k}}$, consider the function $f(t)=\\frac{1+t}{1+t^{2}}$ in interval $(0,1)$. Since $$ f^{\\prime}(t)=\\frac{1-2 t-t^{2}}{\\left(1+t^{2}\\right)^{2}}=\\frac{(\\sqrt{2}+1+t)(\\sqrt{2}-1-t)}{\\left(1+t^{2}\\right)^{2}} $$ the function increases in interval $(0, \\sqrt{2}-1]$ and decreases in $[\\sqrt{2}-1,1)$. Therefore the maximum is at point $t_{0}=\\sqrt{2}-1$ and $$ f(t)=\\frac{1+t}{1+t^{2}} \\leq f\\left(t_{0}\\right)=\\frac{1+\\sqrt{2}}{2}=\\alpha . $$ Applying this to each term on the left-hand side of (1), we obtain $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right) \\leq n \\alpha \\cdot n \\alpha=(n \\alpha)^{2} $$ To estimate $(1-x)(1-y)$ on the right-hand side, consider the function $$ g(t)=\\ln \\left(1-t^{1 / n}\\right)+\\ln \\left(1-(1-t)^{1 / n}\\right) . $$ Substituting $s$ for $1-t$, we have $$ -n g^{\\prime}(t)=\\frac{t^{1 / n-1}}{1-t^{1 / n}}-\\frac{s^{1 / n-1}}{1-s^{1 / n}}=\\frac{1}{s t}\\left(\\frac{(1-t) t^{1 / n}}{1-t^{1 / n}}-\\frac{(1-s) s^{1 / n}}{1-s^{1 / n}}\\right)=\\frac{h(t)-h(s)}{s t} . $$ The function $$ h(t)=t^{1 / n} \\frac{1-t}{1-t^{1 / n}}=\\sum_{i=1}^{n} t^{i / n} $$ is obviously increasing for $t \\in(0,1)$, hence for these values of $t$ we have $$ g^{\\prime}(t)>0 \\Longleftrightarrow h(t)<h(s) \\Longleftrightarrow t<s=1-t \\Longleftrightarrow t<\\frac{1}{2} . $$ Then, the maximum of $g(t)$ in $(0,1)$ is attained at point $t_{1}=1 / 2$ and therefore $$ g(t) \\leq g\\left(\\frac{1}{2}\\right)=2 \\ln \\left(1-2^{-1 / n}\\right), \\quad t \\in(0,1) $$ Substituting $t=x^{n}$, we have $1-t=y^{n},(1-x)(1-y)=\\exp g(t)$ and hence $$ (1-x)(1-y)=\\exp g(t) \\leq\\left(1-2^{-1 / n}\\right)^{2} $$ Combining (2) and (3), we get $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right) \\leq(\\alpha n)^{2} \\cdot 1 \\leq(\\alpha n)^{2} \\frac{\\left(1-2^{-1 / n}\\right)^{2}}{(1-x)(1-y)}=\\frac{\\left(\\alpha n\\left(1-2^{-1 / n}\\right)\\right)^{2}}{(1-x)(1-y)} $$ Applying the inequality $1-\\exp (-t)<t$ for $t=\\frac{\\ln 2}{n}$, we obtain $$ \\alpha n\\left(1-2^{-1 / n}\\right)=\\alpha n\\left(1-\\exp \\left(-\\frac{\\ln 2}{n}\\right)\\right)<\\alpha n \\cdot \\frac{\\ln 2}{n}=\\alpha \\ln 2=\\frac{1+\\sqrt{2}}{2} \\ln 2 . $$ Hence, $$ \\left(\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}\\right)\\left(\\sum_{k=1}^{n} \\frac{1+y^{2 k}}{1+y^{4 k}}\\right)<\\frac{\\left(\\frac{1+\\sqrt{2}}{2} \\ln 2\\right)^{2}}{(1-x)(1-y)} $$ Comment. It is a natural idea to compare the sum $S_{n}(x)=\\sum_{k=1}^{n} \\frac{1+x^{2 k}}{1+x^{4 k}}$ with the integral $I_{n}(x)=$ $\\int_{0}^{n} \\frac{1+x^{2 t}}{1+x^{4 t}} \\mathrm{~d} t$. Though computing the integral is quite standard, many difficulties arise. First, the integrand $\\frac{1+x^{2 k}}{1+x^{4 k}}$ has an increasing segment and, depending on $x$, it can have a decreasing segment as well. So comparing $S_{n}(x)$ and $I_{n}(x)$ is not completely obvious. We can add a term to fix the estimate, e.g. $S_{n} \\leq I_{n}+(\\alpha-1)$, but then the final result will be weak for the small values of $n$. Second, we have to minimize $(1-x)(1-y) I_{n}(x) I_{n}(y)$ which leads to very unpleasant computations. However, by computer search we found that the maximum of $I_{n}(x) I_{n}(y)$ is at $x=y=2^{-1 / n}$, as well as the maximum of $S_{n}(x) S_{n}(y)$, and the latter is less. Hence, one can conjecture that the exact constant which can be put into the numerator on the right-hand side of (1) is $$ \\left(\\ln 2 \\cdot \\int_{0}^{1} \\frac{1+4^{-t}}{1+16^{-t}} \\mathrm{~d} t\\right)^{2}=\\frac{1}{4}\\left(\\frac{1}{2} \\ln \\frac{17}{2}+\\arctan 4-\\frac{\\pi}{4}\\right)^{2} \\approx 0.6484 $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A4", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find all functions $f: \\mathbb{R}^{+} \\rightarrow \\mathbb{R}^{+}$such that $$ f(x+f(y))=f(x+y)+f(y) $$ for all $x, y \\in \\mathbb{R}^{+}$. (Symbol $\\mathbb{R}^{+}$denotes the set of all positive real numbers.) (Thaliand) Answer. $f(x)=2 x$.", "solution": "First we show that $f(y)>y$ for all $y \\in \\mathbb{R}^{+}$. Functional equation (1) yields $f(x+f(y))>f(x+y)$ and hence $f(y) \\neq y$ immediately. If $f(y)<y$ for some $y$, then setting $x=y-f(y)$ we get $$ f(y)=f((y-f(y))+f(y))=f((y-f(y))+y)+f(y)>f(y) $$ contradiction. Therefore $f(y)>y$ for all $y \\in \\mathbb{R}^{+}$. For $x \\in \\mathbb{R}^{+}$define $g(x)=f(x)-x$; then $f(x)=g(x)+x$ and, as we have seen, $g(x)>0$. Transforming (1) for function $g(x)$ and setting $t=x+y$, $$ \\begin{aligned} f(t+g(y)) & =f(t)+f(y) \\\\ g(t+g(y))+t+g(y) & =(g(t)+t)+(g(y)+y) \\end{aligned} $$ and therefore $$ g(t+g(y))=g(t)+y \\quad \\text { for all } t>y>0 $$ Next we prove that function $g(x)$ is injective. Suppose that $g\\left(y_{1}\\right)=g\\left(y_{2}\\right)$ for some numbers $y_{1}, y_{2} \\in \\mathbb{R}^{+}$. Then by $(2)$, $$ g(t)+y_{1}=g\\left(t+g\\left(y_{1}\\right)\\right)=g\\left(t+g\\left(y_{2}\\right)\\right)=g(t)+y_{2} $$ for all $t>\\max \\left\\{y_{1}, y_{2}\\right\\}$. Hence, $g\\left(y_{1}\\right)=g\\left(y_{2}\\right)$ is possible only if $y_{1}=y_{2}$. Now let $u, v$ be arbitrary positive numbers and $t>u+v$. Applying (2) three times, $$ g(t+g(u)+g(v))=g(t+g(u))+v=g(t)+u+v=g(t+g(u+v)) \\text {. } $$ By the injective property we conclude that $t+g(u)+g(v)=t+g(u+v)$, hence $$ g(u)+g(v)=g(u+v) . $$ Since function $g(v)$ is positive, equation (3) also shows that $g$ is an increasing function. Finally we prove that $g(x)=x$. Combining (2) and (3), we obtain $$ g(t)+y=g(t+g(y))=g(t)+g(g(y)) $$ and hence $$ g(g(y))=y $$ Suppose that there exists an $x \\in \\mathbb{R}^{+}$such that $g(x) \\neq x$. By the monotonicity of $g$, if $x>g(x)$ then $g(x)>g(g(x))=x$. Similarly, if $x<g(x)$ then $g(x)<g(g(x))=x$. Both cases lead to contradiction, so there exists no such $x$. We have proved that $g(x)=x$ and therefore $f(x)=g(x)+x=2 x$ for all $x \\in \\mathbb{R}^{+}$. This function indeed satisfies the functional equation (1). Comment. It is well-known that the additive property (3) together with $g(x) \\geq 0$ (for $x>0$ ) imply $g(x)=c x$. So, after proving (3), it is sufficient to test functions $f(x)=(c+1) x$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A4", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find all functions $f: \\mathbb{R}^{+} \\rightarrow \\mathbb{R}^{+}$such that $$ f(x+f(y))=f(x+y)+f(y) $$ for all $x, y \\in \\mathbb{R}^{+}$. (Symbol $\\mathbb{R}^{+}$denotes the set of all positive real numbers.) (Thaliand) Answer. $f(x)=2 x$.", "solution": "We prove that $f(y)>y$ and introduce function $g(x)=f(x)-x>0$ in the same way as in For arbitrary $t>y>0$, substitute $x=t-y$ into (1) to obtain $$ f(t+g(y))=f(t)+f(y) $$ which, by induction, implies $$ f(t+n g(y))=f(t)+n f(y) \\quad \\text { for all } t>y>0, n \\in \\mathbb{N} \\text {. } $$ Take two arbitrary positive reals $y$ and $z$ and a third fixed number $t>\\max \\{y, z\\}$. For each positive integer $k$, let $\\ell_{k}=\\left\\lfloor k \\frac{g(y)}{g(z)}\\right\\rfloor$. Then $t+k g(y)-\\ell_{k} g(z) \\geq t>z$ and, applying (4) twice, $$ \\begin{aligned} f\\left(t+k g(y)-\\ell_{k} g(z)\\right)+\\ell_{k} f(z) & =f(t+k g(y))=f(t)+k f(y) \\\\ 0<\\frac{1}{k} f\\left(t+k g(y)-\\ell_{k} g(z)\\right) & =\\frac{f(t)}{k}+f(y)-\\frac{\\ell_{k}}{k} f(z) . \\end{aligned} $$ As $k \\rightarrow \\infty$ we get $$ 0 \\leq \\lim _{k \\rightarrow \\infty}\\left(\\frac{f(t)}{k}+f(y)-\\frac{\\ell_{k}}{k} f(z)\\right)=f(y)-\\frac{g(y)}{g(z)} f(z)=f(y)-\\frac{f(y)-y}{f(z)-z} f(z) $$ and therefore $$ \\frac{f(y)}{y} \\leq \\frac{f(z)}{z} $$ Exchanging variables $y$ and $z$, we obtain the reverse inequality. Hence, $\\frac{f(y)}{y}=\\frac{f(z)}{z}$ for arbitrary $y$ and $z$; so function $\\frac{f(x)}{x}$ is constant, $f(x)=c x$. Substituting back into (1), we find that $f(x)=c x$ is a solution if and only if $c=2$. So the only solution for the problem is $f(x)=2 x$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A5", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $c>2$, and let $a(1), a(2), \\ldots$ be a sequence of nonnegative real numbers such that $$ a(m+n) \\leq 2 a(m)+2 a(n) \\text { for all } m, n \\geq 1 \\text {, } $$ and $$ a\\left(2^{k}\\right) \\leq \\frac{1}{(k+1)^{c}} \\quad \\text { for all } k \\geq 0 $$ Prove that the sequence $a(n)$ is bounded. (Croatia)", "solution": "For convenience, define $a(0)=0$; then condition (1) persists for all pairs of nonnegative indices. Lemma 1. For arbitrary nonnegative indices $n_{1}, \\ldots, n_{k}$, we have $$ a\\left(\\sum_{i=1}^{k} n_{i}\\right) \\leq \\sum_{i=1}^{k} 2^{i} a\\left(n_{i}\\right) $$ and $$ a\\left(\\sum_{i=1}^{k} n_{i}\\right) \\leq 2 k \\sum_{i=1}^{k} a\\left(n_{i}\\right) $$ Proof. Inequality (3) is proved by induction on $k$. The base case $k=1$ is trivial, while the induction step is provided by $a\\left(\\sum_{i=1}^{k+1} n_{i}\\right)=a\\left(n_{1}+\\sum_{i=2}^{k+1} n_{i}\\right) \\leq 2 a\\left(n_{1}\\right)+2 a\\left(\\sum_{i=1}^{k} n_{i+1}\\right) \\leq 2 a\\left(n_{1}\\right)+2 \\sum_{i=1}^{k} 2^{i} a\\left(n_{i+1}\\right)=\\sum_{i=1}^{k+1} 2^{i} a\\left(n_{i}\\right)$. To establish (4), first the inequality $$ a\\left(\\sum_{i=1}^{2^{d}} n_{i}\\right) \\leq 2^{d} \\sum_{i=1}^{2^{d}} a\\left(n_{i}\\right) $$ can be proved by an obvious induction on $d$. Then, turning to (4), we find an integer $d$ such that $2^{d-1}<k \\leq 2^{d}$ to obtain $$ a\\left(\\sum_{i=1}^{k} n_{i}\\right)=a\\left(\\sum_{i=1}^{k} n_{i}+\\sum_{i=k+1}^{2^{d}} 0\\right) \\leq 2^{d}\\left(\\sum_{i=1}^{k} a\\left(n_{i}\\right)+\\sum_{i=k+1}^{2^{d}} a(0)\\right)=2^{d} \\sum_{i=1}^{k} a\\left(n_{i}\\right) \\leq 2 k \\sum_{i=1}^{k} a\\left(n_{i}\\right) . $$ Fix an increasing unbounded sequence $0=M_{0}<M_{1}<M_{2}<\\ldots$ of real numbers; the exact values will be defined later. Let $n$ be an arbitrary positive integer and write $$ n=\\sum_{i=0}^{d} \\varepsilon_{i} \\cdot 2^{i}, \\quad \\text { where } \\varepsilon_{i} \\in\\{0,1\\} $$ Set $\\varepsilon_{i}=0$ for $i>d$, and take some positive integer $f$ such that $M_{f}>d$. Applying (3), we get $$ a(n)=a\\left(\\sum_{k=1}^{f} \\sum_{M_{k-1} \\leq i<M_{k}} \\varepsilon_{i} \\cdot 2^{i}\\right) \\leq \\sum_{k=1}^{f} 2^{k} a\\left(\\sum_{M_{k-1} \\leq i<M_{k}} \\varepsilon_{i} \\cdot 2^{i}\\right) $$ Note that there are less than $M_{k}-M_{k-1}+1$ integers in interval $\\left[M_{k-1}, M_{k}\\right)$; hence, using (4) we have $$ \\begin{aligned} a(n) & \\leq \\sum_{k=1}^{f} 2^{k} \\cdot 2\\left(M_{k}-M_{k-1}+1\\right) \\sum_{M_{k-1} \\leq i<M_{k}} \\varepsilon_{i} \\cdot a\\left(2^{i}\\right) \\\\ & \\leq \\sum_{k=1}^{f} 2^{k} \\cdot 2\\left(M_{k}-M_{k-1}+1\\right)^{2} \\max _{M_{k-1} \\leq i<M_{k}} a\\left(2^{i}\\right) \\\\ & \\leq \\sum_{k=1}^{f} 2^{k+1}\\left(M_{k}+1\\right)^{2} \\cdot \\frac{1}{\\left(M_{k-1}+1\\right)^{c}}=\\sum_{k=1}^{f}\\left(\\frac{M_{k}+1}{M_{k-1}+1}\\right)^{2} \\frac{2^{k+1}}{\\left(M_{k-1}+1\\right)^{c-2}} . \\end{aligned} $$ Setting $M_{k}=4^{k /(c-2)}-1$, we obtain $$ a(n) \\leq \\sum_{k=1}^{f} 4^{2 /(c-2)} \\frac{2^{k+1}}{\\left(4^{(k-1) /(c-2)}\\right)^{c-2}}=8 \\cdot 4^{2 /(c-2)} \\sum_{k=1}^{f}\\left(\\frac{1}{2}\\right)^{k}<8 \\cdot 4^{2 /(c-2)} $$ and the sequence $a(n)$ is bounded.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A5", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $c>2$, and let $a(1), a(2), \\ldots$ be a sequence of nonnegative real numbers such that $$ a(m+n) \\leq 2 a(m)+2 a(n) \\text { for all } m, n \\geq 1 \\text {, } $$ and $$ a\\left(2^{k}\\right) \\leq \\frac{1}{(k+1)^{c}} \\quad \\text { for all } k \\geq 0 $$ Prove that the sequence $a(n)$ is bounded. (Croatia)", "solution": "Lemma 2. Suppose that $s_{1}, \\ldots, s_{k}$ are positive integers such that $$ \\sum_{i=1}^{k} 2^{-s_{i}} \\leq 1 $$ Then for arbitrary positive integers $n_{1}, \\ldots, n_{k}$ we have $$ a\\left(\\sum_{i=1}^{k} n_{i}\\right) \\leq \\sum_{i=1}^{k} 2^{s_{i}} a\\left(n_{i}\\right) $$ Proof. Apply an induction on $k$. The base cases are $k=1$ (trivial) and $k=2$ (follows from the condition (1)). Suppose that $k>2$. We can assume that $s_{1} \\leq s_{2} \\leq \\cdots \\leq s_{k}$. Note that $$ \\sum_{i=1}^{k-1} 2^{-s_{i}} \\leq 1-2^{-s_{k-1}} $$ since the left-hand side is a fraction with the denominator $2^{s_{k-1}}$, and this fraction is less than 1. Define $s_{k-1}^{\\prime}=s_{k-1}-1$ and $n_{k-1}^{\\prime}=n_{k-1}+n_{k}$; then we have $$ \\sum_{i=1}^{k-2} 2^{-s_{i}}+2^{-s_{k-1}^{\\prime}} \\leq\\left(1-2 \\cdot 2^{-s_{k-1}}\\right)+2^{1-s_{k-1}}=1 . $$ Now, the induction hypothesis can be applied to achieve $$ \\begin{aligned} a\\left(\\sum_{i=1}^{k} n_{i}\\right)=a\\left(\\sum_{i=1}^{k-2} n_{i}+n_{k-1}^{\\prime}\\right) & \\leq \\sum_{i=1}^{k-2} 2^{s_{i}} a\\left(n_{i}\\right)+2^{s_{k-1}^{\\prime}} a\\left(n_{k-1}^{\\prime}\\right) \\\\ & \\leq \\sum_{i=1}^{k-2} 2^{s_{i}} a\\left(n_{i}\\right)+2^{s_{k-1}-1} \\cdot 2\\left(a\\left(n_{k-1}\\right)+a\\left(n_{k}\\right)\\right) \\\\ & \\leq \\sum_{i=1}^{k-2} 2^{s_{i}} a\\left(n_{i}\\right)+2^{s_{k-1}} a\\left(n_{k-1}\\right)+2^{s_{k}} a\\left(n_{k}\\right) . \\end{aligned} $$ Let $q=c / 2>1$. Take an arbitrary positive integer $n$ and write $$ n=\\sum_{i=1}^{k} 2^{u_{i}}, \\quad 0 \\leq u_{1}<u_{2}<\\cdots<u_{k} $$ Choose $s_{i}=\\left\\lfloor\\log _{2}\\left(u_{i}+1\\right)^{q}\\right\\rfloor+d(i=1, \\ldots, k)$ for some integer $d$. We have $$ \\sum_{i=1}^{k} 2^{-s_{i}}=2^{-d} \\sum_{i=1}^{k} 2^{-\\left\\lfloor\\log _{2}\\left(u_{i}+1\\right)^{q}\\right\\rfloor} $$ and we choose $d$ in such a way that $$ \\frac{1}{2}<\\sum_{i=1}^{k} 2^{-s_{i}} \\leq 1 $$ In particular, this implies $$ 2^{d}<2 \\sum_{i=1}^{k} 2^{-\\left\\lfloor\\log _{2}\\left(u_{i}+1\\right)^{q}\\right\\rfloor}<4 \\sum_{i=1}^{k} \\frac{1}{\\left(u_{i}+1\\right)^{q}} $$ Now, by Lemma 2 we obtain $$ \\begin{aligned} a(n)=a\\left(\\sum_{i=1}^{k} 2^{u_{i}}\\right) & \\leq \\sum_{i=1}^{k} 2^{s_{i}} a\\left(2^{u_{i}}\\right) \\leq \\sum_{i=1}^{k} 2^{d}\\left(u_{i}+1\\right)^{q} \\cdot \\frac{1}{\\left(u_{i}+1\\right)^{2 q}} \\\\ & =2^{d} \\sum_{i=1}^{k} \\frac{1}{\\left(u_{i}+1\\right)^{q}}<4\\left(\\sum_{i=1}^{k} \\frac{1}{\\left(u_{i}+1\\right)^{q}}\\right)^{2} \\end{aligned} $$ which is bounded since $q>1$. Comment 1. In fact, Lemma 2 (applied to the case $n_{i}=2^{u_{i}}$ only) provides a sharp bound for any $a(n)$. Actually, let $b(k)=\\frac{1}{(k+1)^{c}}$ and consider the sequence $$ a(n)=\\min \\left\\{\\sum_{i=1}^{k} 2^{s_{i}} b\\left(u_{i}\\right) \\mid k \\in \\mathbb{N}, \\quad \\sum_{i=1}^{k} 2^{-s_{i}} \\leq 1, \\quad \\sum_{i=1}^{k} 2^{u_{i}}=n\\right\\} $$ We show that this sequence satisfies the conditions of the problem. Take two arbitrary indices $m$ and $n$. Let $$ \\begin{aligned} & a(m)=\\sum_{i=1}^{k} 2^{s_{i}} b\\left(u_{i}\\right), \\quad \\sum_{i=1}^{k} 2^{-s_{i}} \\leq 1, \\quad \\sum_{i=1}^{k} 2^{u_{i}}=m ; \\\\ & a(n)=\\sum_{i=1}^{l} 2^{r_{i}} b\\left(w_{i}\\right), \\quad \\sum_{i=1}^{l} 2^{-r_{i}} \\leq 1, \\quad \\sum_{i=1}^{l} 2^{w_{i}}=n . \\end{aligned} $$ Then we have $$ \\sum_{i=1}^{k} 2^{-1-s_{i}}+\\sum_{i=1}^{l} 2^{-1-r_{i}} \\leq \\frac{1}{2}+\\frac{1}{2}=1, \\quad \\sum_{i=1}^{k} 2^{u_{i}}+\\sum_{i=1}^{l} 2^{w_{i}}=m+n $$ so by (5) we obtain $$ a(n+m) \\leq \\sum_{i=1}^{k} 2^{1+s_{i}} b\\left(u_{i}\\right)+\\sum_{i=1}^{l} 2^{1+r_{i}} b\\left(w_{i}\\right)=2 a(m)+2 a(n) . $$ Comment 2. The condition $c>2$ is sharp; we show that the sequence (5) is not bounded if $c \\leq 2$. First, we prove that for an arbitrary $n$ the minimum in (5) is attained with a sequence $\\left(u_{i}\\right)$ consisting of distinct numbers. To the contrary, assume that $u_{k-1}=u_{k}$. Replace $u_{k-1}$ and $u_{k}$ by a single number $u_{k-1}^{\\prime}=u_{k}+1$, and $s_{k-1}$ and $s_{k}$ by $s_{k-1}^{\\prime}=\\min \\left\\{s_{k-1}, s_{k}\\right\\}$. The modified sequences provide a better bound since $$ 2^{s_{k-1}^{\\prime}} b\\left(u_{k-1}^{\\prime}\\right)=2^{s_{k-1}^{\\prime}} b\\left(u_{k}+1\\right)<2^{s_{k-1}} b\\left(u_{k-1}\\right)+2^{s_{k}} b\\left(u_{k}\\right) $$ (we used the fact that $b(k)$ is decreasing). This is impossible. Hence, the claim is proved, and we can assume that the minimum is attained with $u_{1}<\\cdots<u_{k}$; then $$ n=\\sum_{i=1}^{k} 2^{u_{i}} $$ is simply the binary representation of $n$. (In particular, it follows that $a\\left(2^{n}\\right)=b(n)$ for each $n$.) Now we show that the sequence $\\left(a\\left(2^{k}-1\\right)\\right)$ is not bounded. For some $s_{1}, \\ldots, s_{k}$ we have $$ a\\left(2^{k}-1\\right)=a\\left(\\sum_{i=1}^{k} 2^{i-1}\\right)=\\sum_{i=1}^{k} 2^{s_{i}} b(i-1)=\\sum_{i=1}^{k} \\frac{2^{s_{i}}}{i^{c}} . $$ By the Cauchy-Schwarz inequality we get $$ a\\left(2^{k}-1\\right)=a\\left(2^{k}-1\\right) \\cdot 1 \\geq\\left(\\sum_{i=1}^{k} \\frac{2^{s_{i}}}{i^{c}}\\right)\\left(\\sum_{i=1}^{k} \\frac{1}{2^{s_{i}}}\\right) \\geq\\left(\\sum_{i=1}^{k} \\frac{1}{i^{c / 2}}\\right)^{2}, $$ which is unbounded. For $c \\leq 2$, it is also possible to show a concrete counterexample. Actually, one can prove that the sequence $$ a\\left(\\sum_{i=1}^{k} 2^{u_{i}}\\right)=\\sum_{i=1}^{k} \\frac{i}{\\left(u_{i}+1\\right)^{2}} \\quad\\left(0 \\leq u_{1}<\\ldots<u_{k}\\right) $$ satisfies (1) and (2) but is not bounded.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A6", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $a_{1}, a_{2}, \\ldots, a_{100}$ be nonnegative real numbers such that $a_{1}^{2}+a_{2}^{2}+\\ldots+a_{100}^{2}=1$. Prove that $$ a_{1}^{2} a_{2}+a_{2}^{2} a_{3}+\\ldots+a_{100}^{2} a_{1}<\\frac{12}{25} $$ (Poland)", "solution": "Let $S=\\sum_{k=1}^{100} a_{k}^{2} a_{k+1}$. (As usual, we consider the indices modulo 100, e.g. we set $a_{101}=a_{1}$ and $a_{102}=a_{2}$.) Applying the Cauchy-Schwarz inequality to sequences $\\left(a_{k+1}\\right)$ and $\\left(a_{k}^{2}+2 a_{k+1} a_{k+2}\\right)$, and then the AM-GM inequality to numbers $a_{k+1}^{2}$ and $a_{k+2}^{2}$, $$ \\begin{aligned} (3 S)^{2} & =\\left(\\sum_{k=1}^{100} a_{k+1}\\left(a_{k}^{2}+2 a_{k+1} a_{k+2}\\right)\\right)^{2} \\leq\\left(\\sum_{k=1}^{100} a_{k+1}^{2}\\right)\\left(\\sum_{k=1}^{100}\\left(a_{k}^{2}+2 a_{k+1} a_{k+2}\\right)^{2}\\right) \\\\ & =1 \\cdot \\sum_{k=1}^{100}\\left(a_{k}^{2}+2 a_{k+1} a_{k+2}\\right)^{2}=\\sum_{k=1}^{100}\\left(a_{k}^{4}+4 a_{k}^{2} a_{k+1} a_{k+2}+4 a_{k+1}^{2} a_{k+2}^{2}\\right) \\\\ & \\leq \\sum_{k=1}^{100}\\left(a_{k}^{4}+2 a_{k}^{2}\\left(a_{k+1}^{2}+a_{k+2}^{2}\\right)+4 a_{k+1}^{2} a_{k+2}^{2}\\right)=\\sum_{k=1}^{100}\\left(a_{k}^{4}+6 a_{k}^{2} a_{k+1}^{2}+2 a_{k}^{2} a_{k+2}^{2}\\right) . \\end{aligned} $$ Applying the trivial estimates $$ \\sum_{k=1}^{100}\\left(a_{k}^{4}+2 a_{k}^{2} a_{k+1}^{2}+2 a_{k}^{2} a_{k+2}^{2}\\right) \\leq\\left(\\sum_{k=1}^{100} a_{k}^{2}\\right)^{2} \\quad \\text { and } \\quad \\sum_{k=1}^{100} a_{k}^{2} a_{k+1}^{2} \\leq\\left(\\sum_{i=1}^{50} a_{2 i-1}^{2}\\right)\\left(\\sum_{j=1}^{50} a_{2 j}^{2}\\right) $$ we obtain that $$ (3 S)^{2} \\leq\\left(\\sum_{k=1}^{100} a_{k}^{2}\\right)^{2}+4\\left(\\sum_{i=1}^{50} a_{2 i-1}^{2}\\right)\\left(\\sum_{j=1}^{50} a_{2 j}^{2}\\right) \\leq 1+\\left(\\sum_{i=1}^{50} a_{2 i-1}^{2}+\\sum_{j=1}^{50} a_{2 j}^{2}\\right)^{2}=2, $$ hence $$ S \\leq \\frac{\\sqrt{2}}{3} \\approx 0.4714<\\frac{12}{25}=0.48 $$ Comment 1. By applying the Lagrange multiplier method, one can see that the maximum is attained at values of $a_{i}$ satisfying $$ a_{k-1}^{2}+2 a_{k} a_{k+1}=2 \\lambda a_{k} $$ for all $k=1,2, \\ldots, 100$. Though this system of equations seems hard to solve, it can help to find the estimate above; it may suggest to have a closer look at the expression $a_{k-1}^{2} a_{k}+2 a_{k}^{2} a_{k+1}$. Moreover, if the numbers $a_{1}, \\ldots, a_{100}$ satisfy (2), we have equality in (1). (See also Comment 3.) Comment 2. It is natural to ask what is the best constant $c_{n}$ in the inequality $$ a_{1}^{2} a_{2}+a_{2}^{2} a_{3}+\\ldots+a_{n}^{2} a_{1} \\leq c_{n}\\left(a_{1}^{2}+a_{2}^{2}+\\ldots+a_{n}^{2}\\right)^{3 / 2} $$ For $1 \\leq n \\leq 4$ one may prove $c_{n}=1 / \\sqrt{n}$ which is achieved when $a_{1}=a_{2}=\\ldots=a_{n}$. However, the situation changes completely if $n \\geq 5$. In this case we do not know the exact value of $c_{n}$. By computer search it can be found that $c_{n} \\approx 0.4514$ and it is realized for example if $$ a_{1} \\approx 0.5873, \\quad a_{2} \\approx 0.6771, \\quad a_{3} \\approx 0.4224, \\quad a_{4} \\approx 0.1344, \\quad a_{5} \\approx 0.0133 $$ and $a_{k} \\approx 0$ for $k \\geq 6$. This example also proves that $c_{n}>0.4513$. Comment 3. The solution can be improved in several ways to give somewhat better bounds for $c_{n}$. Here we show a variant which proves $c_{n}<0.4589$ for $n \\geq 5$. The value of $c_{n}$ does not change if negative values are also allowed in (3). So the problem is equivalent to maximizing $$ f\\left(a_{1}, a_{2}, \\ldots, a_{n}\\right)=a_{1}^{2} a_{2}+a_{2}^{2} a_{3}+\\ldots+a_{n}^{2} a_{1} $$ on the unit sphere $a_{1}^{2}+a_{2}^{2}+\\ldots+a_{n}^{2}=1$ in $\\mathbb{R}^{n}$. Since the unit sphere is compact, the function has a maximum and we can apply the Lagrange multiplier method; for each maximum point there exists a real number $\\lambda$ such that $$ a_{k-1}^{2}+2 a_{k} a_{k+1}=\\lambda \\cdot 2 a_{k} \\quad \\text { for all } k=1,2, \\ldots, n $$ Then $$ 3 S=\\sum_{k=1}^{n}\\left(a_{k-1}^{2} a_{k}+2 a_{k}^{2} a_{k+1}\\right)=\\sum_{k=1}^{n} 2 \\lambda a_{k}^{2}=2 \\lambda $$ and therefore $$ a_{k-1}^{2}+2 a_{k} a_{k+1}=3 S a_{k} \\quad \\text { for all } k=1,2, \\ldots, n \\text {. } $$ From (4) we can derive $$ 9 S^{2}=\\sum_{k=1}^{n}\\left(3 S a_{k}\\right)^{2}=\\sum_{k=1}^{n}\\left(a_{k-1}^{2}+2 a_{k} a_{k+1}\\right)^{2}=\\sum_{k=1}^{n} a_{k}^{4}+4 \\sum_{k=1}^{n} a_{k}^{2} a_{k+1}^{2}+4 \\sum_{k=1}^{n} a_{k}^{2} a_{k+1} a_{k+2} $$ and $$ 3 S^{2}=\\sum_{k=1}^{n} 3 S a_{k-1}^{2} a_{k}=\\sum_{k=1}^{n} a_{k-1}^{2}\\left(a_{k-1}^{2}+2 a_{k} a_{k+1}\\right)=\\sum_{k=1}^{n} a_{k}^{4}+2 \\sum_{k=1}^{n} a_{k}^{2} a_{k+1} a_{k+2} . $$ Let $p$ be a positive number. Combining (5) and (6) and applying the AM-GM inequality, $$ \\begin{aligned} (9+3 p) S^{2} & =(1+p) \\sum_{k=1}^{n} a_{k}^{4}+4 \\sum_{k=1}^{n} a_{k}^{2} a_{k+1}^{2}+(4+2 p) \\sum_{k=1}^{n} a_{k}^{2} a_{k+1} a_{k+2} \\\\ & \\leq(1+p) \\sum_{k=1}^{n} a_{k}^{4}+4 \\sum_{k=1}^{n} a_{k}^{2} a_{k+1}^{2}+\\sum_{k=1}^{n}\\left(2(1+p) a_{k}^{2} a_{k+2}^{2}+\\frac{(2+p)^{2}}{2(1+p)} a_{k}^{2} a_{k+1}^{2}\\right) \\\\ & =(1+p) \\sum_{k=1}^{n}\\left(a_{k}^{4}+2 a_{k}^{2} a_{k+1}^{2}+2 a_{k}^{2} a_{k+2}^{2}\\right)+\\left(4+\\frac{(2+p)^{2}}{2(1+p)}-2(1+p)\\right) \\sum_{k=1}^{n} a_{k}^{2} a_{k+1}^{2} \\\\ & \\leq(1+p)\\left(\\sum_{k=1}^{n} a_{k}^{2}\\right)^{2}+\\frac{8+4 p-3 p^{2}}{2(1+p)} \\sum_{k=1}^{n} a_{k}^{2} a_{k+1}^{2} \\\\ & =(1+p)+\\frac{8+4 p-3 p^{2}}{2(1+p)} \\sum_{k=1}^{n} a_{k}^{2} a_{k+1}^{2} . \\end{aligned} $$ Setting $p=\\frac{2+2 \\sqrt{7}}{3}$ which is the positive root of $8+4 p-3 p^{2}=0$, we obtain $$ S \\leq \\sqrt{\\frac{1+p}{9+3 p}}=\\sqrt{\\frac{5+2 \\sqrt{7}}{33+6 \\sqrt{7}}} \\approx 0.458879 . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A7", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $n>1$ be an integer. In the space, consider the set $$ S=\\{(x, y, z) \\mid x, y, z \\in\\{0,1, \\ldots, n\\}, x+y+z>0\\} $$ Find the smallest number of planes that jointly contain all $(n+1)^{3}-1$ points of $S$ but none of them passes through the origin. (Netherlands) Answer. $3 n$ planes.", "solution": "It is easy to find $3 n$ such planes. For example, planes $x=i, y=i$ or $z=i$ $(i=1,2, \\ldots, n)$ cover the set $S$ but none of them contains the origin. Another such collection consists of all planes $x+y+z=k$ for $k=1,2, \\ldots, 3 n$. We show that $3 n$ is the smallest possible number. Lemma 1. Consider a nonzero polynomial $P\\left(x_{1}, \\ldots, x_{k}\\right)$ in $k$ variables. Suppose that $P$ vanishes at all points $\\left(x_{1}, \\ldots, x_{k}\\right)$ such that $x_{1}, \\ldots, x_{k} \\in\\{0,1, \\ldots, n\\}$ and $x_{1}+\\cdots+x_{k}>0$, while $P(0,0, \\ldots, 0) \\neq 0$. Then $\\operatorname{deg} P \\geq k n$. Proof. We use induction on $k$. The base case $k=0$ is clear since $P \\neq 0$. Denote for clarity $y=x_{k}$. Let $R\\left(x_{1}, \\ldots, x_{k-1}, y\\right)$ be the residue of $P$ modulo $Q(y)=y(y-1) \\ldots(y-n)$. Polynomial $Q(y)$ vanishes at each $y=0,1, \\ldots, n$, hence $P\\left(x_{1}, \\ldots, x_{k-1}, y\\right)=R\\left(x_{1}, \\ldots, x_{k-1}, y\\right)$ for all $x_{1}, \\ldots, x_{k-1}, y \\in\\{0,1, \\ldots, n\\}$. Therefore, $R$ also satisfies the condition of the Lemma; moreover, $\\operatorname{deg}_{y} R \\leq n$. Clearly, $\\operatorname{deg} R \\leq \\operatorname{deg} P$, so it suffices to prove that $\\operatorname{deg} R \\geq n k$. Now, expand polynomial $R$ in the powers of $y$ : $$ R\\left(x_{1}, \\ldots, x_{k-1}, y\\right)=R_{n}\\left(x_{1}, \\ldots, x_{k-1}\\right) y^{n}+R_{n-1}\\left(x_{1}, \\ldots, x_{k-1}\\right) y^{n-1}+\\cdots+R_{0}\\left(x_{1}, \\ldots, x_{k-1}\\right) $$ We show that polynomial $R_{n}\\left(x_{1}, \\ldots, x_{k-1}\\right)$ satisfies the condition of the induction hypothesis. Consider the polynomial $T(y)=R(0, \\ldots, 0, y)$ of degree $\\leq n$. This polynomial has $n$ roots $y=1, \\ldots, n$; on the other hand, $T(y) \\not \\equiv 0$ since $T(0) \\neq 0$. Hence $\\operatorname{deg} T=n$, and its leading coefficient is $R_{n}(0,0, \\ldots, 0) \\neq 0$. In particular, in the case $k=1$ we obtain that coefficient $R_{n}$ is nonzero. Similarly, take any numbers $a_{1}, \\ldots, a_{k-1} \\in\\{0,1, \\ldots, n\\}$ with $a_{1}+\\cdots+a_{k-1}>0$. Substituting $x_{i}=a_{i}$ into $R\\left(x_{1}, \\ldots, x_{k-1}, y\\right)$, we get a polynomial in $y$ which vanishes at all points $y=0, \\ldots, n$ and has degree $\\leq n$. Therefore, this polynomial is null, hence $R_{i}\\left(a_{1}, \\ldots, a_{k-1}\\right)=0$ for all $i=0,1, \\ldots, n$. In particular, $R_{n}\\left(a_{1}, \\ldots, a_{k-1}\\right)=0$. Thus, the polynomial $R_{n}\\left(x_{1}, \\ldots, x_{k-1}\\right)$ satisfies the condition of the induction hypothesis. So, we have $\\operatorname{deg} R_{n} \\geq(k-1) n$ and $\\operatorname{deg} P \\geq \\operatorname{deg} R \\geq \\operatorname{deg} R_{n}+n \\geq k n$. Now we can finish the solution. Suppose that there are $N$ planes covering all the points of $S$ but not containing the origin. Let their equations be $a_{i} x+b_{i} y+c_{i} z+d_{i}=0$. Consider the polynomial $$ P(x, y, z)=\\prod_{i=1}^{N}\\left(a_{i} x+b_{i} y+c_{i} z+d_{i}\\right) $$ It has total degree $N$. This polynomial has the property that $P\\left(x_{0}, y_{0}, z_{0}\\right)=0$ for any $\\left(x_{0}, y_{0}, z_{0}\\right) \\in S$, while $P(0,0,0) \\neq 0$. Hence by Lemma 1 we get $N=\\operatorname{deg} P \\geq 3 n$, as desired. Comment 1. There are many other collections of $3 n$ planes covering the set $S$ but not covering the origin.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "A7", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $n>1$ be an integer. In the space, consider the set $$ S=\\{(x, y, z) \\mid x, y, z \\in\\{0,1, \\ldots, n\\}, x+y+z>0\\} $$ Find the smallest number of planes that jointly contain all $(n+1)^{3}-1$ points of $S$ but none of them passes through the origin. (Netherlands) Answer. $3 n$ planes.", "solution": "We present a different proof of the main Lemma 1. Here we confine ourselves to the case $k=3$, which is applied in the solution, and denote the variables by $x, y$ and $z$. (The same proof works for the general statement as well.) The following fact is known with various proofs; we provide one possible proof for the completeness. Lemma 2. For arbitrary integers $0 \\leq m<n$ and for an arbitrary polynomial $P(x)$ of degree $m$, $$ \\sum_{k=0}^{n}(-1)^{k}\\left(\\begin{array}{l} n \\\\ k \\end{array}\\right) P(k)=0 $$ Proof. We use an induction on $n$. If $n=1$, then $P(x)$ is a constant polynomial, hence $P(1)-P(0)=0$, and the base is proved. For the induction step, define $P_{1}(x)=P(x+1)-P(x)$. Then clearly $\\operatorname{deg} P_{1}=\\operatorname{deg} P-1=$ $m-1<n-1$, hence by the induction hypothesis we get $$ \\begin{aligned} 0 & =-\\sum_{k=0}^{n-1}(-1)^{k}\\left(\\begin{array}{c} n-1 \\\\ k \\end{array}\\right) P_{1}(k)=\\sum_{k=0}^{n-1}(-1)^{k}\\left(\\begin{array}{c} n-1 \\\\ k \\end{array}\\right)(P(k)-P(k+1)) \\\\ & =\\sum_{k=0}^{n-1}(-1)^{k}\\left(\\begin{array}{c} n-1 \\\\ k \\end{array}\\right) P(k)-\\sum_{k=0}^{n-1}(-1)^{k}\\left(\\begin{array}{c} n-1 \\\\ k \\end{array}\\right) P(k+1) \\\\ & =\\sum_{k=0}^{n-1}(-1)^{k}\\left(\\begin{array}{c} n-1 \\\\ k \\end{array}\\right) P(k)+\\sum_{k=1}^{n}(-1)^{k}\\left(\\begin{array}{c} n-1 \\\\ k-1 \\end{array}\\right) P(k) \\\\ & =P(0)+\\sum_{k=1}^{n-1}(-1)^{k}\\left(\\left(\\begin{array}{c} n-1 \\\\ k-1 \\end{array}\\right)+\\left(\\begin{array}{c} n-1 \\\\ k \\end{array}\\right)\\right) P(k)+(-1)^{n} P(n)=\\sum_{k=0}^{n}(-1)^{k}\\left(\\begin{array}{l} n \\\\ k \\end{array}\\right) P(k) . \\end{aligned} $$ Now return to the proof of Lemma 1. Suppose, to the contrary, that $\\operatorname{deg} P=N<3 n$. Consider the sum $$ \\Sigma=\\sum_{i=0}^{n} \\sum_{j=0}^{n} \\sum_{k=0}^{n}(-1)^{i+j+k}\\left(\\begin{array}{l} n \\\\ i \\end{array}\\right)\\left(\\begin{array}{l} n \\\\ j \\end{array}\\right)\\left(\\begin{array}{l} n \\\\ k \\end{array}\\right) P(i, j, k) $$ The only nonzero term in this sum is $P(0,0,0)$ and its coefficient is $\\left(\\begin{array}{l}n \\\\ 0\\end{array}\\right)^{3}=1$; therefore $\\Sigma=P(0,0,0) \\neq 0$. On the other hand, if $P(x, y, z)=\\sum_{\\alpha+\\beta+\\gamma \\leq N} p_{\\alpha, \\beta, \\gamma} x^{\\alpha} y^{\\beta} z^{\\gamma}$, then $$ \\begin{aligned} \\Sigma & =\\sum_{i=0}^{n} \\sum_{j=0}^{n} \\sum_{k=0}^{n}(-1)^{i+j+k}\\left(\\begin{array}{c} n \\\\ i \\end{array}\\right)\\left(\\begin{array}{c} n \\\\ j \\end{array}\\right)\\left(\\begin{array}{l} n \\\\ k \\end{array}\\right) \\sum_{\\alpha+\\beta+\\gamma \\leq N} p_{\\alpha, \\beta, \\gamma} i^{\\alpha} j^{\\beta} k^{\\gamma} \\\\ & =\\sum_{\\alpha+\\beta+\\gamma \\leq N} p_{\\alpha, \\beta, \\gamma}\\left(\\sum_{i=0}^{n}(-1)^{i}\\left(\\begin{array}{c} n \\\\ i \\end{array}\\right) i^{\\alpha}\\right)\\left(\\sum_{j=0}^{n}(-1)^{j}\\left(\\begin{array}{l} n \\\\ j \\end{array}\\right) j^{\\beta}\\right)\\left(\\sum_{k=0}^{n}(-1)^{k}\\left(\\begin{array}{l} n \\\\ k \\end{array}\\right) k^{\\gamma}\\right) . \\end{aligned} $$ Consider an arbitrary term in this sum. We claim that it is zero. Since $N<3 n$, one of three inequalities $\\alpha<n, \\beta<n$ or $\\gamma<n$ is valid. For the convenience, suppose that $\\alpha<n$. Applying Lemma 2 to polynomial $x^{\\alpha}$, we get $\\sum_{i=0}^{n}(-1)^{i}\\left(\\begin{array}{c}n \\\\ i\\end{array}\\right) i^{\\alpha}=0$, hence the term is zero as required. This yields $\\Sigma=0$ which is a contradiction. Therefore, $\\operatorname{deg} P \\geq 3 n$. Comment 2. The proof does not depend on the concrete coefficients in Lemma 2. Instead of this Lemma, one can simply use the fact that there exist numbers $\\alpha_{0}, \\alpha_{1}, \\ldots, \\alpha_{n}\\left(\\alpha_{0} \\neq 0\\right)$ such that $$ \\sum_{k=0}^{n} \\alpha_{k} k^{m}=0 \\quad \\text { for every } 0 \\leq m<n $$ This is a system of homogeneous linear equations in variables $\\alpha_{i}$. Since the number of equations is less than the number of variables, the only nontrivial thing is that there exists a solution with $\\alpha_{0} \\neq 0$. It can be shown in various ways.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C1", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $n>1$ be an integer. Find all sequences $a_{1}, a_{2}, \\ldots, a_{n^{2}+n}$ satisfying the following conditions: (a) $a_{i} \\in\\{0,1\\}$ for all $1 \\leq i \\leq n^{2}+n$; (b) $a_{i+1}+a_{i+2}+\\ldots+a_{i+n}<a_{i+n+1}+a_{i+n+2}+\\ldots+a_{i+2 n}$ for all $0 \\leq i \\leq n^{2}-n$. (Serbia) Answer. Such a sequence is unique. It can be defined as follows: $$ a_{u+v n}=\\left\\{\\begin{array}{ll} 0, & u+v \\leq n, \\\\ 1, & u+v \\geq n+1 \\end{array} \\quad \\text { for all } 1 \\leq u \\leq n \\text { and } 0 \\leq v \\leq n\\right. $$ The terms can be arranged into blocks of length $n$ as $$ (\\underbrace{0 \\ldots 0}_{n})(\\underbrace{0 \\ldots 0}_{n-1} 1)(\\underbrace{0 \\ldots 0}_{n-2} 11) \\ldots(\\underbrace{0 \\ldots 0}_{n-v} \\underbrace{1 \\ldots 1}_{v}) \\ldots(0 \\underbrace{1 \\ldots 1}_{n-1})(\\underbrace{1 \\ldots 1}_{n}) . $$", "solution": "Consider a sequence $\\left(a_{i}\\right)$ satisfying the conditions. For arbitrary integers $0 \\leq$ $k \\leq l \\leq n^{2}+n$ denote $S(k, l]=a_{k+1}+\\cdots+a_{l}$. (If $k=l$ then $S(k, l]=0$.) Then condition (b) can be rewritten as $S(i, i+n]<S(i+n, i+2 n]$ for all $0 \\leq i \\leq n^{2}-n$. Notice that for $0 \\leq k \\leq l \\leq m \\leq n^{2}+n$ we have $S(k, m]=S(k, l]+S(l, m]$. By condition (b), $$ 0 \\leq S(0, n]<S(n, 2 n]<\\cdots<S\\left(n^{2}, n^{2}+n\\right] \\leq n $$ We have only $n+1$ distinct integers in the interval $[0, n]$; hence, $$ S(v n,(v+1) n]=v \\quad \\text { for all } 0 \\leq v \\leq n \\text {. } $$ In particular, $S(0, n]=0$ and $S\\left(n^{2}, n^{2}+n\\right]=n$, therefore $$ \\begin{aligned} a_{1} & =a_{2}=\\ldots=a_{n}=0 \\\\ a_{n^{2}+1} & =a_{n^{2}+2}=\\ldots=a_{n^{2}+n}=1 . \\end{aligned} $$ Subdivide sequence $\\left(a_{i}\\right)$ into $n+1$ blocks, each consisting of $n$ consecutive terms, and number them from 0 to $n$. We show by induction on $v$ that the $v$ th blocks has the form $$ (\\underbrace{0 \\ldots 0}_{n-v} \\underbrace{1 \\ldots 1}_{v}) . $$ The base case $v=0$ is provided by (3). Consider the $v$ th block for $v>0$. By (2), it contains some \"ones\". Let the first \"one\" in this block be at the $u$ th position (that is, $\\left.a_{u+v n}=1\\right)$. By the induction hypothesis, the $(v-1)$ th and $v$ th blocks of $\\left(a_{i}\\right)$ have the form $$ (\\underbrace{0 \\ldots 0 \\ldots 0}_{n-v+1} \\underbrace{1 \\ldots 1}_{v-1})(\\underbrace{0 \\ldots 0}_{u-1} 1 * \\ldots *), $$ where each star can appear to be any binary digit. Observe that $u \\leq n-v+1$, since the sum in this block is $v$. Then, the fragment of length $n$ bracketed above has exactly $(v-1)+1$ ones, i. e. $S(u+(v-1) n, u+v n]=v$. Hence, $$ v=S(u+(v-1) n, u+v n]<S(u+v n, u+(v+1) n]<\\cdots<S\\left(u+(n-1) n, u+n^{2}\\right] \\leq n $$ we have $n-v+1$ distinct integers in the interval $[v, n]$, therefore $S(u+(t-1) n, u+t n]=t$ for each $t=v, \\ldots, n$. Thus, the end of sequence $\\left(a_{i}\\right)$ looks as following: 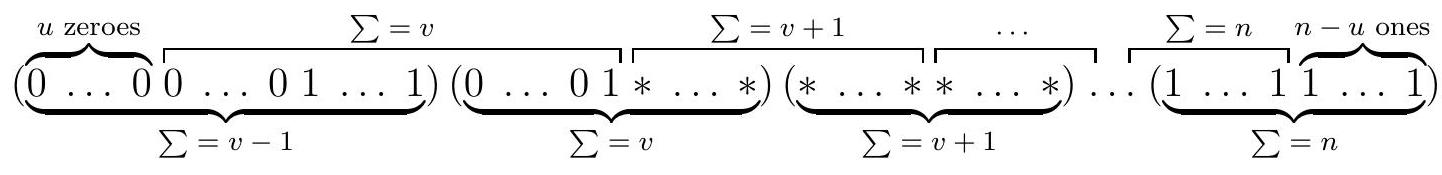 (each bracketed fragment contains $n$ terms). Computing in two ways the sum of all digits above, we obtain $n-u=v-1$ and $u=n-v+1$. Then, the first $n-v$ terms in the $v$ th block are zeroes, and the next $v$ terms are ones, due to the sum of all terms in this block. The statement is proved. We are left to check that the sequence obtained satisfies the condition. Notice that $a_{i} \\leq a_{i+n}$ for all $1 \\leq i \\leq n^{2}$. Moreover, if $1 \\leq u \\leq n$ and $0 \\leq v \\leq n-1$, then $a_{u+v n}<a_{u+v n+n}$ exactly when $u+v=n$. In this case we have $u+v n=n+v(n-1)$. Consider now an arbitrary index $0 \\leq i \\leq n^{2}-n$. Clearly, there exists an integer $v$ such that $n+v(n-1) \\in[i+1, i+n]$. Then, applying the above inequalities we obtain that condition (b) is valid.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C1", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $n>1$ be an integer. Find all sequences $a_{1}, a_{2}, \\ldots, a_{n^{2}+n}$ satisfying the following conditions: (a) $a_{i} \\in\\{0,1\\}$ for all $1 \\leq i \\leq n^{2}+n$; (b) $a_{i+1}+a_{i+2}+\\ldots+a_{i+n}<a_{i+n+1}+a_{i+n+2}+\\ldots+a_{i+2 n}$ for all $0 \\leq i \\leq n^{2}-n$. (Serbia) Answer. Such a sequence is unique. It can be defined as follows: $$ a_{u+v n}=\\left\\{\\begin{array}{ll} 0, & u+v \\leq n, \\\\ 1, & u+v \\geq n+1 \\end{array} \\quad \\text { for all } 1 \\leq u \\leq n \\text { and } 0 \\leq v \\leq n\\right. $$ The terms can be arranged into blocks of length $n$ as $$ (\\underbrace{0 \\ldots 0}_{n})(\\underbrace{0 \\ldots 0}_{n-1} 1)(\\underbrace{0 \\ldots 0}_{n-2} 11) \\ldots(\\underbrace{0 \\ldots 0}_{n-v} \\underbrace{1 \\ldots 1}_{v}) \\ldots(0 \\underbrace{1 \\ldots 1}_{n-1})(\\underbrace{1 \\ldots 1}_{n}) . $$", "solution": "Similarly to $$ S\\left(0, n^{2}+n\\right]=S(0, n]+S(n, 2 n]+\\ldots+S\\left(n^{2}, n^{2}+n\\right]=0+1+\\ldots+n $$ For an arbitrary integer $0 \\leq u \\leq n$, consider the numbers $$ S(u, u+n]<S(u+n, u+2 n]<\\ldots<S\\left(u+(n-1) n, u+n^{2}\\right] . $$ They are $n$ distinct integers from the $n+1$ possible values $0,1,2, \\ldots, n$. Denote by $m$ the \"missing\" value which is not listed. We determine $m$ from $S\\left(0, n^{2}+n\\right]$. Write this sum as $S\\left(0, n^{2}+n\\right]=S(0, u]+S(u, u+n]+S(u+n, u+2 n]+\\ldots+S\\left(u+(n-1) n, u+n^{2}\\right]+S\\left(u+n^{2}, n^{2}+n\\right]$. Since $a_{1}=a_{2}=\\ldots=a_{u}=0$ and $a_{u+n^{2}+1}=\\ldots=a_{n^{2}+n}=1$, we have $S(0, u]=0$ and $S\\left(u+n^{2}, n+n^{2}\\right]=n-u$. Then $$ 0+1+\\ldots+n=S\\left(0, n^{2}+n\\right]=0+((0+1+\\ldots+n)-m)+(n-u), $$ so $m=n-u$. Hence, the numbers listed in (5) are $0,1, \\ldots, n-u-1$ and $n-u+1, \\ldots, n$, respectively, therefore $$ S(u+v n, u+(v+1) n]=\\left\\{\\begin{array}{ll} v, & v \\leq n-u-1, \\\\ v+1, & v \\geq n-u \\end{array} \\quad \\text { for all } 0 \\leq u \\leq n, 0 \\leq v \\leq n-1\\right. $$ Conditions (6), together with (3), provide a system of linear equations in variables $a_{i}$. Now we solve this system and show that the solution is unique and satisfies conditions (a) and (b). First, observe that any solution of the system (3), (6) satisfies the condition (b). By the construction, equations (6) immediately imply (5). On the other hand, all inequalities mentioned in condition (b) are included into the chain (5) for some value of $u$. Next, note that the system (3), (6) is redundant. The numbers $S(k n,(k+1) n]$, where $1 \\leq k \\leq n-1$, appear twice in (6). For $u=0$ and $v=k$ we have $v \\leq n-u-1$, and (6) gives $S(k n,(k+1) n]=v=k$. For $u=n$ and $v=k-1$ we have $v \\geq n-u$ and we obtain the same value, $S(k n,(k+1) n]=v+1=k$. Therefore, deleting one equation from each redundant pair, we can make every sum $S(k, k+n]$ appear exactly once on the left-hand side in (6). Now, from (3), (6), the sequence $\\left(a_{i}\\right)$ can be reconstructed inductively by $a_{1}=a_{2}=\\ldots=a_{n-1}=0, \\quad a_{k+n}=S(k, k+n]-\\left(a_{k+1}+a_{k+2}+\\ldots+a_{k+n-1}\\right) \\quad\\left(0 \\leq k \\leq n^{2}\\right)$, taking the values of $S(k, k+n]$ from (6). This means first that there exists at most one solution of our system. Conversely, the constructed sequence obviously satisfies all equations (3), (6) (the only missing equation is $a_{n}=0$, which follows from $S(0, n]=0$ ). Hence it satisfies condition (b), and we are left to check condition (a) only. For arbitrary integers $1 \\leq u, t \\leq n$ we get $$ \\begin{aligned} a_{u+t n}-a_{u+(t-1) n}= & S(u+(t-1) n, u+t n]-S((u-1)+(t-1) n,(u-1)+t n] \\\\ & = \\begin{cases}(t-1)-(t-1)=0, & t \\leq n-u, \\\\ t-(t-1)=1, & t=n-u+1, \\\\ t-t=0, & t \\geq n-u+2 .\\end{cases} \\end{aligned} $$ Since $a_{u}=0$, we have $$ a_{u+v n}=a_{u+v n}-a_{u}=\\sum_{t=1}^{v}\\left(a_{u+t n}-a_{u+(t-1) n}\\right) $$ for all $1 \\leq u, v \\leq n$. If $v<n-u+1$ then all terms are 0 on the right-hand side. If $v \\geq n-u+1$, then variable $t$ attains the value $n-u+1$ once. Hence, $$ a_{u+v n}= \\begin{cases}0, & u+v \\leq n \\\\ 1, & u+v \\geq n+1\\end{cases} $$ according with (1). Note that the formula is valid for $v=0$ as well. Finally, we presented the direct formula for $\\left(a_{i}\\right)$, and we have proved that it satisfies condition (a). So, the solution is complete.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square. (Japan)", "solution": "Call the directions of the sides of the square horizontal and vertical. A horizontal or vertical line, which intersects the interior of the square but does not intersect the interior of any rectangle, will be called a splitting line. A rectangle having no point on the boundary of the square will be called an interior rectangle. Suppose, to the contrary, that there exists a dissection of the square into more than one rectangle, such that no interior rectangle and no splitting line appear. Consider such a dissection with the least possible number of rectangles. Notice that this number of rectangles is greater than 2, otherwise their common side provides a splitting line. If there exist two rectangles having a common side, then we can replace them by their union (see Figure 1). The number of rectangles was greater than 2, so in a new dissection it is greater than 1. Clearly, in the new dissection, there is also no splitting line as well as no interior rectangle. This contradicts the choice of the original dissection. Denote the initial square by $A B C D$, with $A$ and $B$ being respectively the lower left and lower right vertices. Consider those two rectangles $a$ and $b$ containing vertices $A$ and $B$, respectively. (Note that $a \\neq b$, otherwise its top side provides a splitting line.) We can assume that the height of $a$ is not greater than that of $b$. Then consider the rectangle $c$ neighboring to the lower right corner of $a$ (it may happen that $c=b$ ). By aforementioned, the heights of $a$ and $c$ are distinct. Then two cases are possible.  Figure 1 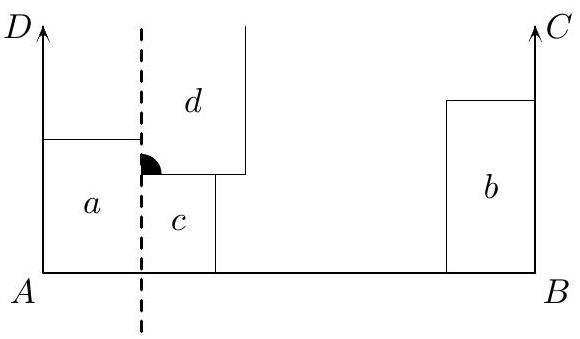 Figure 2 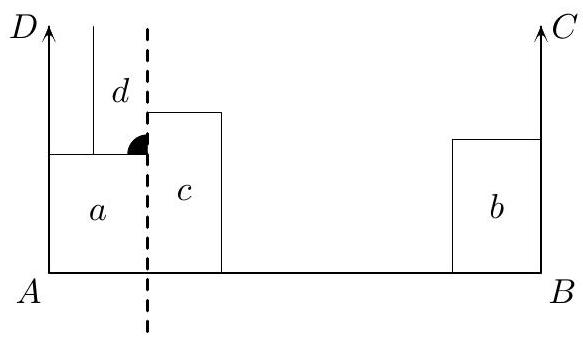 Figure 3 Case 1. The height of $c$ is less than that of $a$. Consider the rectangle $d$ which is adjacent to both $a$ and $c$, i. e. the one containing the angle marked in Figure 2. This rectangle has no common point with $B C$ (since $a$ is not higher than $b$ ), as well as no common point with $A B$ or with $A D$ (obviously). Then $d$ has a common point with $C D$, and its left side provides a splitting line. Contradiction. Case 2. The height of $c$ is greater than that of $a$. Analogously, consider the rectangle $d$ containing the angle marked on Figure 3. It has no common point with $A D$ (otherwise it has a common side with $a$ ), as well as no common point with $A B$ or with $B C$ (obviously). Then $d$ has a common point with $C D$. Hence its right side provides a splitting line, and we get the contradiction again.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square. (Japan)", "solution": "Again, we suppose the contrary. Consider an arbitrary counterexample. Then we know that each rectangle is attached to at least one side of the square. Observe that a rectangle cannot be attached to two opposite sides, otherwise one of its sides lies on a splitting line. We say that two rectangles are opposite if they are attached to opposite sides of $A B C D$. We claim that there exist two opposite rectangles having a common point. Consider the union $L$ of all rectangles attached to the left. Assume, to the contrary, that $L$ has no common point with the rectangles attached to the right. Take a polygonal line $p$ connecting the top and the bottom sides of the square and passing close from the right to the boundary of $L$ (see Figure 4). Then all its points belong to the rectangles attached either to the top or to the bottom. Moreover, the upper end-point of $p$ belongs to a rectangle attached to the top, and the lower one belongs to an other rectangle attached to the bottom. Hence, there is a point on $p$ where some rectangles attached to the top and to the bottom meet each other. So, there always exists a pair of neighboring opposite rectangles. 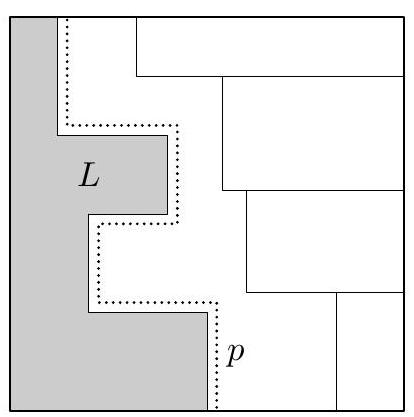 Figure 4 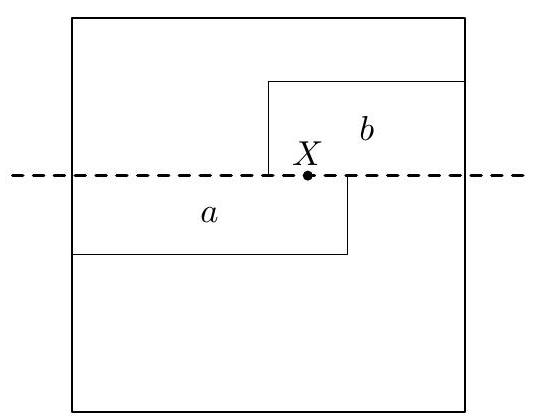 Figure 5 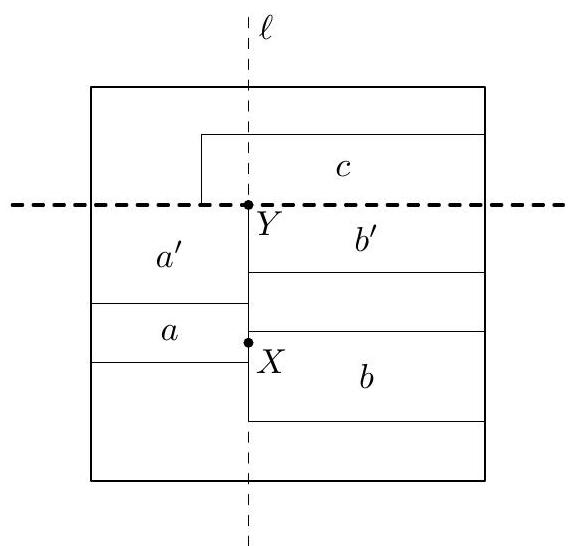 Figure 6 Now, take two opposite neighboring rectangles $a$ and $b$. We can assume that $a$ is attached to the left and $b$ is attached to the right. Let $X$ be their common point. If $X$ belongs to their horizontal sides (in particular, $X$ may appear to be a common vertex of $a$ and $b$ ), then these sides provide a splitting line (see Figure 5). Otherwise, $X$ lies on the vertical sides. Let $\\ell$ be the line containing these sides. Since $\\ell$ is not a splitting line, it intersects the interior of some rectangle. Let $c$ be such a rectangle, closest to $X$; we can assume that $c$ lies above $X$. Let $Y$ be the common point of $\\ell$ and the bottom side of $c$ (see Figure 6). Then $Y$ is also a vertex of two rectangles lying below $c$. So, let $Y$ be the upper-right and upper-left corners of the rectangles $a^{\\prime}$ and $b^{\\prime}$, respectively. Then $a^{\\prime}$ and $b^{\\prime}$ are situated not lower than $a$ and $b$, respectively (it may happen that $a=a^{\\prime}$ or $b=b^{\\prime}$ ). We claim that $a^{\\prime}$ is attached to the left. If $a=a^{\\prime}$ then of course it is. If $a \\neq a^{\\prime}$ then $a^{\\prime}$ is above $a$, below $c$ and to the left from $b^{\\prime}$. Hence, it can be attached to the left only. Analogously, $b^{\\prime}$ is attached to the right. Now, the top sides of these two rectangles pass through $Y$, hence they provide a splitting line again. This last contradiction completes the proof.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C3", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Find all positive integers $n$, for which the numbers in the set $S=\\{1,2, \\ldots, n\\}$ can be colored red and blue, with the following condition being satisfied: the set $S \\times S \\times S$ contains exactly 2007 ordered triples $(x, y, z)$ such that (i) $x, y, z$ are of the same color and (ii) $x+y+z$ is divisible by $n$. (Netherlands) Answer. $n=69$ and $n=84$.", "solution": "Suppose that the numbers $1,2, \\ldots, n$ are colored red and blue. Denote by $R$ and $B$ the sets of red and blue numbers, respectively; let $|R|=r$ and $|B|=b=n-r$. Call a triple $(x, y, z) \\in S \\times S \\times S$ monochromatic if $x, y, z$ have the same color, and bichromatic otherwise. Call a triple $(x, y, z)$ divisible if $x+y+z$ is divisible by $n$. We claim that there are exactly $r^{2}-r b+b^{2}$ divisible monochromatic triples. For any pair $(x, y) \\in S \\times S$ there exists a unique $z_{x, y} \\in S$ such that the triple $\\left(x, y, z_{x, y}\\right)$ is divisible; so there are exactly $n^{2}$ divisible triples. Furthermore, if a divisible triple $(x, y, z)$ is bichromatic, then among $x, y, z$ there are either one blue and two red numbers, or vice versa. In both cases, exactly one of the pairs $(x, y),(y, z)$ and $(z, x)$ belongs to the set $R \\times B$. Assign such pair to the triple $(x, y, z)$. Conversely, consider any pair $(x, y) \\in R \\times B$, and denote $z=z_{x, y}$. Since $x \\neq y$, the triples $(x, y, z),(y, z, x)$ and $(z, x, y)$ are distinct, and $(x, y)$ is assigned to each of them. On the other hand, if $(x, y)$ is assigned to some triple, then this triple is clearly one of those mentioned above. So each pair in $R \\times B$ is assigned exactly three times. Thus, the number of bichromatic divisible triples is three times the number of elements in $R \\times B$, and the number of monochromatic ones is $n^{2}-3 r b=(r+b)^{2}-3 r b=r^{2}-r b+b^{2}$, as claimed. So, to find all values of $n$ for which the desired coloring is possible, we have to find all $n$, for which there exists a decomposition $n=r+b$ with $r^{2}-r b+b^{2}=2007$. Therefore, $9 \\mid r^{2}-r b+b^{2}=(r+b)^{2}-3 r b$. From this it consequently follows that $3|r+b, 3| r b$, and then $3|r, 3| b$. Set $r=3 s, b=3 c$. We can assume that $s \\geq c$. We have $s^{2}-s c+c^{2}=223$. Furthermore, $$ 892=4\\left(s^{2}-s c+c^{2}\\right)=(2 c-s)^{2}+3 s^{2} \\geq 3 s^{2} \\geq 3 s^{2}-3 c(s-c)=3\\left(s^{2}-s c+c^{2}\\right)=669 $$ so $297 \\geq s^{2} \\geq 223$ and $17 \\geq s \\geq 15$. If $s=15$ then $$ c(15-c)=c(s-c)=s^{2}-\\left(s^{2}-s c+c^{2}\\right)=15^{2}-223=2 $$ which is impossible for an integer $c$. In a similar way, if $s=16$ then $c(16-c)=33$, which is also impossible. Finally, if $s=17$ then $c(17-c)=66$, and the solutions are $c=6$ and $c=11$. Hence, $(r, b)=(51,18)$ or $(r, b)=(51,33)$, and the possible values of $n$ are $n=51+18=69$ and $n=51+33=84$. Comment. After the formula for the number of monochromatic divisible triples is found, the solution can be finished in various ways. The one presented is aimed to decrease the number of considered cases.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C4", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $A_{0}=\\left(a_{1}, \\ldots, a_{n}\\right)$ be a finite sequence of real numbers. For each $k \\geq 0$, from the sequence $A_{k}=\\left(x_{1}, \\ldots, x_{n}\\right)$ we construct a new sequence $A_{k+1}$ in the following way. 1. We choose a partition $\\{1, \\ldots, n\\}=I \\cup J$, where $I$ and $J$ are two disjoint sets, such that the expression $$ \\left|\\sum_{i \\in I} x_{i}-\\sum_{j \\in J} x_{j}\\right| $$ attains the smallest possible value. (We allow the sets $I$ or $J$ to be empty; in this case the corresponding sum is 0 .) If there are several such partitions, one is chosen arbitrarily. 2. We set $A_{k+1}=\\left(y_{1}, \\ldots, y_{n}\\right)$, where $y_{i}=x_{i}+1$ if $i \\in I$, and $y_{i}=x_{i}-1$ if $i \\in J$. Prove that for some $k$, the sequence $A_{k}$ contains an element $x$ such that $|x| \\geq n / 2$. (Iran)", "solution": "Lemma. Suppose that all terms of the sequence $\\left(x_{1}, \\ldots, x_{n}\\right)$ satisfy the inequality $\\left|x_{i}\\right|<a$. Then there exists a partition $\\{1,2, \\ldots, n\\}=I \\cup J$ into two disjoint sets such that $$ \\left|\\sum_{i \\in I} x_{i}-\\sum_{j \\in J} x_{j}\\right|<a $$ Proof. Apply an induction on $n$. The base case $n=1$ is trivial. For the induction step, consider a sequence $\\left(x_{1}, \\ldots, x_{n}\\right)(n>1)$. By the induction hypothesis there exists a splitting $\\{1, \\ldots, n-1\\}=I^{\\prime} \\cup J^{\\prime}$ such that $$ \\left|\\sum_{i \\in I^{\\prime}} x_{i}-\\sum_{j \\in J^{\\prime}} x_{j}\\right|<a $$ For convenience, suppose that $\\sum_{i \\in I^{\\prime}} x_{i} \\geq \\sum_{j \\in J^{\\prime}} x_{j}$. If $x_{n} \\geq 0$ then choose $I=I^{\\prime}, J=J \\cup\\{n\\}$; otherwise choose $I=I^{\\prime} \\cup\\{n\\}, J=J^{\\prime}$. In both cases, we have $\\sum_{i \\in I^{\\prime}} x_{i}-\\sum_{j \\in J^{\\prime}} x_{j} \\in[0, a)$ and $\\left|x_{n}\\right| \\in[0, a)$; hence $$ \\sum_{i \\in I} x_{i}-\\sum_{j \\in J} x_{j}=\\sum_{i \\in I^{\\prime}} x_{i}-\\sum_{j \\in J^{\\prime}} x_{j}-\\left|x_{n}\\right| \\in(-a, a) $$ as desired. Let us turn now to the problem. To the contrary, assume that for all $k$, all the numbers in $A_{k}$ lie in interval $(-n / 2, n / 2)$. Consider an arbitrary sequence $A_{k}=\\left(b_{1}, \\ldots, b_{n}\\right)$. To obtain the term $b_{i}$, we increased and decreased number $a_{i}$ by one several times. Therefore $b_{i}-a_{i}$ is always an integer, and there are not more than $n$ possible values for $b_{i}$. So, there are not more than $n^{n}$ distinct possible sequences $A_{k}$, and hence two of the sequences $A_{1}, A_{2}, \\ldots, A_{n^{n}+1}$ should be identical, say $A_{p}=A_{q}$ for some $p<q$. For any positive integer $k$, let $S_{k}$ be the sum of squares of elements in $A_{k}$. Consider two consecutive sequences $A_{k}=\\left(x_{1}, \\ldots, x_{n}\\right)$ and $A_{k+1}=\\left(y_{1}, \\ldots, y_{n}\\right)$. Let $\\{1,2, \\ldots, n\\}=I \\cup J$ be the partition used in this step - that is, $y_{i}=x_{i}+1$ for all $i \\in I$ and $y_{j}=x_{j}-1$ for all $j \\in J$. Since the value of $\\left|\\sum_{i \\in I} x_{i}-\\sum_{j \\in J} x_{j}\\right|$ is the smallest possible, the Lemma implies that it is less than $n / 2$. Then we have $S_{k+1}-S_{k}=\\sum_{i \\in I}\\left(\\left(x_{i}+1\\right)^{2}-x_{i}^{2}\\right)+\\sum_{j \\in J}\\left(\\left(x_{j}-1\\right)^{2}-x_{j}^{2}\\right)=n+2\\left(\\sum_{i \\in I} x_{i}-\\sum_{j \\in J} x_{j}\\right)>n-2 \\cdot \\frac{n}{2}=0$. Thus we obtain $S_{q}>S_{q-1}>\\cdots>S_{p}$. This is impossible since $A_{p}=A_{q}$ and hence $S_{p}=S_{q}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "In the Cartesian coordinate plane define the strip $S_{n}=\\{(x, y) \\mid n \\leq x<n+1\\}$ for every integer $n$. Assume that each strip $S_{n}$ is colored either red or blue, and let $a$ and $b$ be two distinct positive integers. Prove that there exists a rectangle with side lengths $a$ and $b$ such that its vertices have the same color. (Romania)", "solution": "If $S_{n}$ and $S_{n+a}$ have the same color for some integer $n$, then we can choose the rectangle with vertices $(n, 0) \\in S_{n},(n, b) \\in S_{n},(n+a, 0) \\in S_{n+a}$, and $(n+a, b) \\in S_{n+a}$, and we are done. So it can be assumed that $S_{n}$ and $S_{n+a}$ have opposite colors for each $n$. Similarly, it also can be assumed that $S_{n}$ and $S_{n+b}$ have opposite colors. Then, by induction on $|p|+|q|$, we obtain that for arbitrary integers $p$ and $q$, strips $S_{n}$ and $S_{n+p a+q b}$ have the same color if $p+q$ is even, and these two strips have opposite colors if $p+q$ is odd. Let $d=\\operatorname{gcd}(a, b), a_{1}=a / d$ and $b_{1}=b / d$. Apply the result above for $p=b_{1}$ and $q=-a_{1}$. The strips $S_{0}$ and $S_{0+b_{1} a-a_{1} b}$ are identical and therefore they have the same color. Hence, $a_{1}+b_{1}$ is even. By the construction, $a_{1}$ and $b_{1}$ are coprime, so this is possible only if both are odd. Without loss of generality, we can assume $a>b$. Then $a_{1}>b_{1} \\geq 1$, so $a_{1} \\geq 3$. Choose integers $k$ and $\\ell$ such that $k a_{1}-\\ell b_{1}=1$ and therefore $k a-\\ell b=d$. Since $a_{1}$ and $b_{1}$ are odd, $k+\\ell$ is odd as well. Hence, for every integer $n$, strips $S_{n}$ and $S_{n+k a-\\ell b}=S_{n+d}$ have opposite colors. This also implies that the coloring is periodic with period $2 d$, i.e. strips $S_{n}$ and $S_{n+2 d}$ have the same color for every $n$.  Figure 1 We will construct the desired rectangle $A B C D$ with $A B=C D=a$ and $B C=A D=b$ in a position such that vertex $A$ lies on the $x$-axis, and the projection of side $A B$ onto the $x$-axis is of length $2 d$ (see Figure 1). This is possible since $a=a_{1} d>2 d$. The coordinates of the vertices will have the forms $$ A=(t, 0), \\quad B=\\left(t+2 d, y_{1}\\right), \\quad C=\\left(u+2 d, y_{2}\\right), \\quad D=\\left(u, y_{3}\\right) . $$ Let $\\varphi=\\sqrt{a_{1}^{2}-4}$. By Pythagoras' theorem, $$ y_{1}=B B_{0}=\\sqrt{a^{2}-4 d^{2}}=d \\sqrt{a_{1}^{2}-4}=d \\varphi \\text {. } $$ So, by the similar triangles $A D D_{0}$ and $B A B_{0}$, we have the constraint $$ u-t=A D_{0}=\\frac{A D}{A B} \\cdot B B_{0}=\\frac{b d}{a} \\varphi $$ for numbers $t$ and $u$. Computing the numbers $y_{2}$ and $y_{3}$ is not required since they have no effect to the colors. Observe that the number $\\varphi$ is irrational, because $\\varphi^{2}$ is an integer, but $\\varphi$ is not: $a_{1}>\\varphi \\geq$ $\\sqrt{a_{1}^{2}-2 a_{1}+2}>a_{1}-1$. By the periodicity, points $A$ and $B$ have the same color; similarly, points $C$ and $D$ have the same color. Furthermore, these colors depend only on the values of $t$ and $u$. So it is sufficient to choose numbers $t$ and $u$ such that vertices $A$ and $D$ have the same color. Let $w$ be the largest positive integer such that there exist $w$ consecutive strips $S_{n_{0}}, S_{n_{0}+1}, \\ldots$, $S_{n_{0}+w-1}$ with the same color, say red. (Since $S_{n_{0}+d}$ must be blue, we have $w \\leq d$.) We will choose $t$ from the interval $\\left(n_{0}, n_{0}+w\\right)$.  Figure 2 Consider the interval $I=\\left(n_{0}+\\frac{b d}{a} \\varphi, n_{0}+\\frac{b d}{a} \\varphi+w\\right)$ on the $x$-axis (see Figure 2). Its length is $w$, and the end-points are irrational. Therefore, this interval intersects $w+1$ consecutive strips. Since at most $w$ consecutive strips may have the same color, interval $I$ must contain both red and blue points. Choose $u \\in I$ such that the line $x=u$ is red and set $t=u-\\frac{b d}{a} \\varphi$, according to the constraint (1). Then $t \\in\\left(n_{0}, n_{0}+w\\right)$ and $A=(t, 0)$ is red as well as $D=\\left(u, y_{3}\\right)$. Hence, variables $u$ and $t$ can be set such that they provide a rectangle with four red vertices. Comment. The statement is false for squares, i.e. in the case $a=b$. If strips $S_{2 k a}, S_{2 k a+1}, \\ldots$, $S_{(2 k+1) a-1}$ are red, and strips $S_{(2 k+1) a}, S_{(2 k+1) a+1}, \\ldots, S_{(2 k+2) a-1}$ are blue for every integer $k$, then each square of size $a \\times a$ has at least one red and at least one blue vertex as well.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C6", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "In a mathematical competition some competitors are friends; friendship is always mutual. Call a group of competitors a clique if each two of them are friends. The number of members in a clique is called its size. It is known that the largest size of cliques is even. Prove that the competitors can be arranged in two rooms such that the largest size of cliques in one room is the same as the largest size of cliques in the other room. (Russia)", "solution": "We present an algorithm to arrange the competitors. Let the two rooms be Room $A$ and Room B. We start with an initial arrangement, and then we modify it several times by sending one person to the other room. At any state of the algorithm, $A$ and $B$ denote the sets of the competitors in the rooms, and $c(A)$ and $c(B)$ denote the largest sizes of cliques in the rooms, respectively. Step 1. Let $M$ be one of the cliques of largest size, $|M|=2 m$. Send all members of $M$ to Room $A$ and all other competitors to Room B. Since $M$ is a clique of the largest size, we have $c(A)=|M| \\geq c(B)$. Step 2. While $c(A)>c(B)$, send one person from Room $A$ to Room $B$.  Note that $c(A)>c(B)$ implies that Room $A$ is not empty. In each step, $c(A)$ decreases by one and $c(B)$ increases by at most one. So at the end we have $c(A) \\leq c(B) \\leq c(A)+1$. We also have $c(A)=|A| \\geq m$ at the end. Otherwise we would have at least $m+1$ members of $M$ in Room $B$ and at most $m-1$ in Room $A$, implying $c(B)-c(A) \\geq(m+1)-(m-1)=2$. Step 3. Let $k=c(A)$. If $c(B)=k$ then $S T O P$. If we reached $c(A)=c(B)=k$ then we have found the desired arrangement. In all other cases we have $c(B)=k+1$. From the estimate above we also know that $k=|A|=|A \\cap M| \\geq m$ and $|B \\cap M| \\leq m$. Step 4. If there exists a competitor $x \\in B \\cap M$ and a clique $C \\subset B$ such that $|C|=k+1$ and $x \\notin C$, then move $x$ to Room $A$ and $S T O P$.  After moving $x$ back to Room $A$, we will have $k+1$ members of $M$ in Room $A$, thus $c(A)=k+1$. Due to $x \\notin C, c(B)=|C|$ is not decreased, and after this step we have $c(A)=c(B)=k+1$. If there is no such competitor $x$, then in Room $B$, all cliques of size $k+1$ contain $B \\cap M$ as a subset. Step 5. While $c(B)=k+1$, choose a clique $C \\subset B$ such that $|C|=k+1$ and move one member of $C \\backslash M$ to Room $A$.  Note that $|C|=k+1>m \\geq|B \\cap M|$, so $C \\backslash M$ cannot be empty. Every time we move a single person from Room $B$ to Room $A$, so $c(B)$ decreases by at most 1. Hence, at the end of this loop we have $c(B)=k$. In Room $A$ we have the clique $A \\cap M$ with size $|A \\cap M|=k$ thus $c(A) \\geq k$. We prove that there is no clique of larger size there. Let $Q \\subset A$ be an arbitrary clique. We show that $|Q| \\leq k$.  In Room $A$, and specially in set $Q$, there can be two types of competitors: - Some members of $M$. Since $M$ is a clique, they are friends with all members of $B \\cap M$. - Competitors which were moved to Room $A$ in Step 5. Each of them has been in a clique with $B \\cap M$ so they are also friends with all members of $B \\cap M$. Hence, all members of $Q$ are friends with all members of $B \\cap M$. Sets $Q$ and $B \\cap M$ are cliques themselves, so $Q \\cup(B \\cap M)$ is also a clique. Since $M$ is a clique of the largest size, $$ |M| \\geq|Q \\cup(B \\cap M)|=|Q|+|B \\cap M|=|Q|+|M|-|A \\cap M| $$ therefore $$ |Q| \\leq|A \\cap M|=k $$ Finally, after Step 5 we have $c(A)=c(B)=k$. Comment. Obviously, the statement is false without the assumption that the largest clique size is even.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C7", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $\\alpha<\\frac{3-\\sqrt{5}}{2}$ be a positive real number. Prove that there exist positive integers $n$ and $p>\\alpha \\cdot 2^{n}$ for which one can select $2 p$ pairwise distinct subsets $S_{1}, \\ldots, S_{p}, T_{1}, \\ldots, T_{p}$ of the set $\\{1,2, \\ldots, n\\}$ such that $S_{i} \\cap T_{j} \\neq \\varnothing$ for all $1 \\leq i, j \\leq p$. (Austria)", "solution": "Let $k$ and $m$ be positive integers (to be determined later) and set $n=k m$. Decompose the set $\\{1,2, \\ldots, n\\}$ into $k$ disjoint subsets, each of size $m$; denote these subsets by $A_{1}, \\ldots, A_{k}$. Define the following families of sets: $$ \\begin{aligned} \\mathcal{S} & =\\left\\{S \\subset\\{1,2, \\ldots, n\\}: \\forall i S \\cap A_{i} \\neq \\varnothing\\right\\} \\\\ \\mathcal{T}_{1} & =\\left\\{T \\subset\\{1,2, \\ldots, n\\}: \\quad \\exists i A_{i} \\subset T\\right\\}, \\quad \\mathcal{T}=\\mathcal{T}_{1} \\backslash \\mathcal{S} . \\end{aligned} $$ For each set $T \\in \\mathcal{T} \\subset \\mathcal{T}_{1}$, there exists an index $1 \\leq i \\leq k$ such that $A_{i} \\subset T$. Then for all $S \\in \\mathcal{S}$, $S \\cap T \\supset S \\cap A_{i} \\neq \\varnothing$. Hence, each $S \\in \\mathcal{S}$ and each $T \\in \\mathcal{T}$ have at least one common element. Below we show that the numbers $m$ and $k$ can be chosen such that $|\\mathcal{S}|,|\\mathcal{T}|>\\alpha \\cdot 2^{n}$. Then, choosing $p=\\min \\{|\\mathcal{S}|,|\\mathcal{T}|\\}$, one can select the desired $2 p$ sets $S_{1}, \\ldots, S_{p}$ and $T_{1}, \\ldots, T_{p}$ from families $\\mathcal{S}$ and $\\mathcal{T}$, respectively. Since families $\\mathcal{S}$ and $\\mathcal{T}$ are disjoint, sets $S_{i}$ and $T_{j}$ will be pairwise distinct. To count the sets $S \\in \\mathcal{S}$, observe that each $A_{i}$ has $2^{m}-1$ nonempty subsets so we have $2^{m}-1$ choices for $S \\cap A_{i}$. These intersections uniquely determine set $S$, so $$ |\\mathcal{S}|=\\left(2^{m}-1\\right)^{k} $$ Similarly, if a set $H \\subset\\{1,2, \\ldots, n\\}$ does not contain a certain set $A_{i}$ then we have $2^{m}-1$ choices for $H \\cap A_{i}$ : all subsets of $A_{i}$, except $A_{i}$ itself. Therefore, the complement of $\\mathcal{T}_{1}$ contains $\\left(2^{m}-1\\right)^{k}$ sets and $$ \\left|\\mathcal{T}_{1}\\right|=2^{k m}-\\left(2^{m}-1\\right)^{k} . $$ Next consider the family $\\mathcal{S} \\backslash \\mathcal{T}_{1}$. If a set $S$ intersects all $A_{i}$ but does not contain any of them, then there exists $2^{m}-2$ possible values for each $S \\cap A_{i}$ : all subsets of $A_{i}$ except $\\varnothing$ and $A_{i}$. Therefore the number of such sets $S$ is $\\left(2^{m}-2\\right)^{k}$, so $$ \\left|\\mathcal{S} \\backslash \\mathcal{T}_{1}\\right|=\\left(2^{m}-2\\right)^{k} $$ From (1), (2), and (3) we obtain $$ |\\mathcal{T}|=\\left|\\mathcal{T}_{1}\\right|-\\left|\\mathcal{S} \\cap \\mathcal{T}_{1}\\right|=\\left|\\mathcal{T}_{1}\\right|-\\left(|\\mathcal{S}|-\\left|\\mathcal{S} \\backslash \\mathcal{T}_{1}\\right|\\right)=2^{k m}-2\\left(2^{m}-1\\right)^{k}+\\left(2^{m}-2\\right)^{k} $$ Let $\\delta=\\frac{3-\\sqrt{5}}{2}$ and $k=k(m)=\\left[2^{m} \\log \\frac{1}{\\delta}\\right]$. Then $$ \\lim _{m \\rightarrow \\infty} \\frac{|\\mathcal{S}|}{2^{k m}}=\\lim _{m \\rightarrow \\infty}\\left(1-\\frac{1}{2^{m}}\\right)^{k}=\\exp \\left(-\\lim _{m \\rightarrow \\infty} \\frac{k}{2^{m}}\\right)=\\delta $$ and similarly $$ \\lim _{m \\rightarrow \\infty} \\frac{|\\mathcal{T}|}{2^{k m}}=1-2 \\lim _{m \\rightarrow \\infty}\\left(1-\\frac{1}{2^{m}}\\right)^{k}+\\lim _{m \\rightarrow \\infty}\\left(1-\\frac{2}{2^{m}}\\right)^{k}=1-2 \\delta+\\delta^{2}=\\delta $$ Hence, if $m$ is sufficiently large then $\\frac{|\\mathcal{S}|}{2^{m k}}$ and $\\frac{|\\mathcal{T}|}{2^{m k}}$ are greater than $\\alpha$ (since $\\alpha<\\delta$ ). So $|\\mathcal{S}|,|\\mathcal{T}|>\\alpha \\cdot 2^{m k}=\\alpha \\cdot 2^{n}$. Comment. It can be proved that the constant $\\frac{3-\\sqrt{5}}{2}$ is sharp. Actually, if $S_{1}, \\ldots, S_{p}, T_{1}, \\ldots, T_{p}$ are distinct subsets of $\\{1,2, \\ldots, n\\}$ such that each $S_{i}$ intersects each $T_{j}$, then $p<\\frac{3-\\sqrt{5}}{2} \\cdot 2^{n}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "C8", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Given a convex $n$-gon $P$ in the plane. For every three vertices of $P$, consider the triangle determined by them. Call such a triangle good if all its sides are of unit length. Prove that there are not more than $\\frac{2}{3} n$ good triangles. (Ukraine)", "solution": "Consider all good triangles containing a certain vertex $A$. The other two vertices of any such triangle lie on the circle $\\omega_{A}$ with unit radius and center $A$. Since $P$ is convex, all these vertices lie on an arc of angle less than $180^{\\circ}$. Let $L_{A} R_{A}$ be the shortest such arc, oriented clockwise (see Figure 1). Each of segments $A L_{A}$ and $A R_{A}$ belongs to a unique good triangle. We say that the good triangle with side $A L_{A}$ is assigned counterclockwise to $A$, and the second one, with side $A R_{A}$, is assigned clockwise to $A$. In those cases when there is a single good triangle containing vertex $A$, this triangle is assigned to $A$ twice. There are at most two assignments to each vertex of the polygon. (Vertices which do not belong to any good triangle have no assignment.) So the number of assignments is at most $2 n$. Consider an arbitrary good triangle $A B C$, with vertices arranged clockwise. We prove that $A B C$ is assigned to its vertices at least three times. Then, denoting the number of good triangles by $t$, we obtain that the number $K$ of all assignments is at most $2 n$, while it is not less than $3 t$. Then $3 t \\leq K \\leq 2 n$, as required. Actually, we prove that triangle $A B C$ is assigned either counterclockwise to $C$ or clockwise to $B$. Then, by the cyclic symmetry of the vertices, we obtain that triangle $A B C$ is assigned either counterclockwise to $A$ or clockwise to $C$, and either counterclockwise to $B$ or clockwise to $A$, providing the claim.  Figure 1  Figure 2 Assume, to the contrary, that $L_{C} \\neq A$ and $R_{B} \\neq A$. Denote by $A^{\\prime}, B^{\\prime}, C^{\\prime}$ the intersection points of circles $\\omega_{A}, \\omega_{B}$ and $\\omega_{C}$, distinct from $A, B, C$ (see Figure 2). Let $C L_{C} L_{C}^{\\prime}$ be the good triangle containing $C L_{C}$. Observe that the angle of $\\operatorname{arc} L_{C} A$ is less than $120^{\\circ}$. Then one of the points $L_{C}$ and $L_{C}^{\\prime}$ belongs to $\\operatorname{arc} B^{\\prime} A$ of $\\omega_{C}$; let this point be $X$. In the case when $L_{C}=B^{\\prime}$ and $L_{C}^{\\prime}=A$, choose $X=B^{\\prime}$. Analogously, considering the good triangle $B R_{B}^{\\prime} R_{B}$ which contains $B R_{B}$ as an edge, we see that one of the points $R_{B}$ and $R_{B}^{\\prime}$ lies on arc $A C^{\\prime}$ of $\\omega_{B}$. Denote this point by $Y, Y \\neq A$. Then angles $X A Y, Y A B, B A C$ and $C A X$ (oriented clockwise) are not greater than $180^{\\circ}$. Hence, point $A$ lies in quadrilateral $X Y B C$ (either in its interior or on segment $X Y$ ). This is impossible, since all these five points are vertices of $P$. Hence, each good triangle has at least three assignments, and the statement is proved. Comment 1. Considering a diameter $A B$ of the polygon, one can prove that every good triangle containing either $A$ or $B$ has at least four assignments. This observation leads to $t \\leq\\left\\lfloor\\frac{2}{3}(n-1)\\right\\rfloor$. Comment 2. The result $t \\leq\\left\\lfloor\\frac{2}{3}(n-1)\\right\\rfloor$ is sharp. To construct a polygon with $n=3 k+1$ vertices and $t=2 k$ triangles, take a rhombus $A B_{1} C_{1} D_{1}$ with unit side length and $\\angle B_{1}=60^{\\circ}$. Then rotate it around $A$ by small angles obtaining rhombi $A B_{2} C_{2} D_{2}, \\ldots, A B_{k} C_{k} D_{k}$ (see Figure 3). The polygon $A B_{1} \\ldots B_{k} C_{1} \\ldots C_{k} D_{1} \\ldots D_{k}$ has $3 k+1$ vertices and contains $2 k$ good triangles. The construction for $n=3 k$ and $n=3 k-1$ can be obtained by deleting vertices $D_{n}$ and $D_{n-1}$. 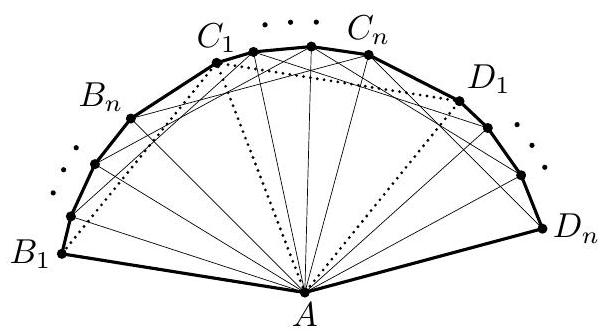 Figure 3", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G1", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "In triangle $A B C$, the angle bisector at vertex $C$ intersects the circumcircle and the perpendicular bisectors of sides $B C$ and $C A$ at points $R, P$, and $Q$, respectively. The midpoints of $B C$ and $C A$ are $S$ and $T$, respectively. Prove that triangles $R Q T$ and $R P S$ have the same area. (Czech Republic)", "solution": "If $A C=B C$ then triangle $A B C$ is isosceles, triangles $R Q T$ and $R P S$ are symmetric about the bisector $C R$ and the statement is trivial. If $A C \\neq B C$ then it can be assumed without loss of generality that $A C<B C$.  Denote the circumcenter by $O$. The right triangles $C T Q$ and $C S P$ have equal angles at vertex $C$, so they are similar, $\\angle C P S=\\angle C Q T=\\angle O Q P$ and $$ \\frac{Q T}{P S}=\\frac{C Q}{C P} $$ Let $\\ell$ be the perpendicular bisector of chord $C R$; of course, $\\ell$ passes through the circumcenter $O$. Due to the equal angles at $P$ and $Q$, triangle $O P Q$ is isosceles with $O P=O Q$. Then line $\\ell$ is the axis of symmetry in this triangle as well. Therefore, points $P$ and $Q$ lie symmetrically on line segment $C R$, $$ R P=C Q \\quad \\text { and } \\quad R Q=C P $$ Triangles $R Q T$ and $R P S$ have equal angles at vertices $Q$ and $P$, respectively. Then $$ \\frac{\\operatorname{area}(R Q T)}{\\operatorname{area}(R P S)}=\\frac{\\frac{1}{2} \\cdot R Q \\cdot Q T \\cdot \\sin \\angle R Q T}{\\frac{1}{2} \\cdot R P \\cdot P S \\cdot \\sin \\angle R P S}=\\frac{R Q}{R P} \\cdot \\frac{Q T}{P S} $$ Substituting (1) and (2), $$ \\frac{\\operatorname{area}(R Q T)}{\\operatorname{area}(R P S)}=\\frac{R Q}{R P} \\cdot \\frac{Q T}{P S}=\\frac{C P}{C Q} \\cdot \\frac{C Q}{C P}=1 $$ Hence, $\\operatorname{area}(R Q T)=\\operatorname{area}(R S P)$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G1", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "In triangle $A B C$, the angle bisector at vertex $C$ intersects the circumcircle and the perpendicular bisectors of sides $B C$ and $C A$ at points $R, P$, and $Q$, respectively. The midpoints of $B C$ and $C A$ are $S$ and $T$, respectively. Prove that triangles $R Q T$ and $R P S$ have the same area. (Czech Republic)", "solution": "Assume again $A C<B C$. Denote the circumcenter by $O$, and let $\\gamma$ be the angle at $C$. Similarly to the first solution, from right triangles $C T Q$ and $C S P$ we obtain that $\\angle O P Q=\\angle O Q P=90^{\\circ}-\\frac{\\gamma}{2}$. Then triangle $O P Q$ is isosceles, $O P=O Q$ and moreover $\\angle P O Q=\\gamma$. As is well-known, point $R$ is the midpoint of $\\operatorname{arc} A B$ and $\\angle R O A=\\angle B O R=\\gamma$.  Consider the rotation around point $O$ by angle $\\gamma$. This transform moves $A$ to $R, R$ to $B$ and $Q$ to $P$; hence triangles $R Q A$ and $B P R$ are congruent and they have the same area. Triangles $R Q T$ and $R Q A$ have $R Q$ as a common side, so the ratio between their areas is $$ \\frac{\\operatorname{area}(R Q T)}{\\operatorname{area}(R Q A)}=\\frac{d(T, C R)}{d(A, C R)}=\\frac{C T}{C A}=\\frac{1}{2} $$ $(d(X, Y Z)$ denotes the distance between point $X$ and line $Y Z)$. It can be obtained similarly that $$ \\frac{\\operatorname{area}(R P S)}{\\operatorname{area}(B P R)}=\\frac{C S}{C B}=\\frac{1}{2} $$ Now the proof can be completed as $$ \\operatorname{area}(R Q T)=\\frac{1}{2} \\operatorname{area}(R Q A)=\\frac{1}{2} \\operatorname{area}(B P R)=\\operatorname{area}(R P S) $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G2", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Given an isosceles triangle $A B C$ with $A B=A C$. The midpoint of side $B C$ is denoted by $M$. Let $X$ be a variable point on the shorter arc $M A$ of the circumcircle of triangle $A B M$. Let $T$ be the point in the angle domain $B M A$, for which $\\angle T M X=90^{\\circ}$ and $T X=B X$. Prove that $\\angle M T B-\\angle C T M$ does not depend on $X$. (Canada)", "solution": "Let $N$ be the midpoint of segment $B T$ (see Figure 1). Line $X N$ is the axis of symmetry in the isosceles triangle $B X T$, thus $\\angle T N X=90^{\\circ}$ and $\\angle B X N=\\angle N X T$. Moreover, in triangle $B C T$, line $M N$ is the midline parallel to $C T$; hence $\\angle C T M=\\angle N M T$. Due to the right angles at points $M$ and $N$, these points lie on the circle with diameter $X T$. Therefore, $$ \\angle M T B=\\angle M T N=\\angle M X N \\quad \\text { and } \\quad \\angle C T M=\\angle N M T=\\angle N X T=\\angle B X N $$ Hence $$ \\angle M T B-\\angle C T M=\\angle M X N-\\angle B X N=\\angle M X B=\\angle M A B $$ which does not depend on $X$.  Figure 1  Figure 2", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G2", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Given an isosceles triangle $A B C$ with $A B=A C$. The midpoint of side $B C$ is denoted by $M$. Let $X$ be a variable point on the shorter arc $M A$ of the circumcircle of triangle $A B M$. Let $T$ be the point in the angle domain $B M A$, for which $\\angle T M X=90^{\\circ}$ and $T X=B X$. Prove that $\\angle M T B-\\angle C T M$ does not depend on $X$. (Canada)", "solution": "Let $S$ be the reflection of point $T$ over $M$ (see Figure 2). Then $X M$ is the perpendicular bisector of $T S$, hence $X B=X T=X S$, and $X$ is the circumcenter of triangle $B S T$. Moreover, $\\angle B S M=\\angle C T M$ since they are symmetrical about $M$. Then $$ \\angle M T B-\\angle C T M=\\angle S T B-\\angle B S T=\\frac{\\angle S X B-\\angle B X T}{2} . $$ Observe that $\\angle S X B=\\angle S X T-\\angle B X T=2 \\angle M X T-\\angle B X T$, so $$ \\angle M T B-\\angle C T M=\\frac{2 \\angle M X T-2 \\angle B X T}{2}=\\angle M X B=\\angle M A B, $$ which is constant.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G3", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "The diagonals of a trapezoid $A B C D$ intersect at point $P$. Point $Q$ lies between the parallel lines $B C$ and $A D$ such that $\\angle A Q D=\\angle C Q B$, and line $C D$ separates points $P$ and $Q$. Prove that $\\angle B Q P=\\angle D A Q$. (Ukraine)", "solution": "Let $t=\\frac{A D}{B C}$. Consider the homothety $h$ with center $P$ and scale $-t$. Triangles $P D A$ and $P B C$ are similar with ratio $t$, hence $h(B)=D$ and $h(C)=A$.  Let $Q^{\\prime}=h(Q)$ (see Figure 1). Then points $Q, P$ and $Q^{\\prime}$ are obviously collinear. Points $Q$ and $P$ lie on the same side of $A D$, as well as on the same side of $B C$; hence $Q^{\\prime}$ and $P$ are also on the same side of $h(B C)=A D$, and therefore $Q$ and $Q^{\\prime}$ are on the same side of $A D$. Moreover, points $Q$ and $C$ are on the same side of $B D$, while $Q^{\\prime}$ and $A$ are on the opposite side (see Figure above). By the homothety, $\\angle A Q^{\\prime} D=\\angle C Q B=\\angle A Q D$, hence quadrilateral $A Q^{\\prime} Q D$ is cyclic. Then $$ \\angle D A Q=\\angle D Q^{\\prime} Q=\\angle D Q^{\\prime} P=\\angle B Q P $$ (the latter equality is valid by the homothety again). Comment. The statement of the problem is a limit case of the following result. In an arbitrary quadrilateral $A B C D$, let $P=A C \\cap B D, I=A D \\cap B C$, and let $Q$ be an arbitrary point which is not collinear with any two of points $A, B, C, D$. Then $\\angle A Q D=\\angle C Q B$ if and only if $\\angle B Q P=\\angle I Q A$ (angles are oriented; see Figure below to the left). In the special case of the trapezoid, $I$ is an ideal point and $\\angle D A Q=\\angle I Q A=\\angle B Q P$.  Let $a=Q A, b=Q B, c=Q C, d=Q D, i=Q I$ and $p=Q P$. Let line $Q A$ intersect lines $B C$ and $B D$ at points $U$ and $V$, respectively. On lines $B C$ and $B D$ we have $$ (a b c i)=(U B C I) \\quad \\text { and } \\quad(b a d p)=(a b p d)=(V B P D) \\text {. } $$ Projecting from $A$, we get $$ (a b c i)=(U B C I)=(V B P D)=(b a d p) . $$ Suppose that $\\angle A Q D=\\angle C Q B$. Let line $p^{\\prime}$ be the reflection of line $i$ about the bisector of angle $A Q B$. Then by symmetry we have $\\left(b a d p^{\\prime}\\right)=(a b c i)=(b a d p)$. Hence $p=p^{\\prime}$, as desired. The converse statement can be proved analogously.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G4", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Consider five points $A, B, C, D, E$ such that $A B C D$ is a parallelogram and $B C E D$ is a cyclic quadrilateral. Let $\\ell$ be a line passing through $A$, and let $\\ell$ intersect segment $D C$ and line $B C$ at points $F$ and $G$, respectively. Suppose that $E F=E G=E C$. Prove that $\\ell$ is the bisector of angle $D A B$. (Luxembourg)", "solution": "If $C F=C G$, then $\\angle F G C=\\angle G F C$, hence $\\angle G A B=\\angle G F C=\\angle F G C=\\angle F A D$, and $\\ell$ is a bisector. Assume that $C F<G C$. Let $E K$ and $E L$ be the altitudes in the isosceles triangles $E C F$ and $E G C$, respectively. Then in the right triangles $E K F$ and $E L C$ we have $E F=E C$ and $$ K F=\\frac{C F}{2}<\\frac{G C}{2}=L C, $$ So $$ K E=\\sqrt{E F^{2}-K F^{2}}>\\sqrt{E C^{2}-L C^{2}}=L E . $$ Since quadrilateral $B C E D$ is cyclic, we have $\\angle E D C=\\angle E B C$, so the right triangles $B E L$ and $D E K$ are similar. Then $K E>L E$ implies $D K>B L$, and hence $$ D F=D K-K F>B L-L C=B C=A D \\text {. } $$ But triangles $A D F$ and $G C F$ are similar, so we have $1>\\frac{A D}{D F}=\\frac{G C}{C F}$; this contradicts our assumption. The case $C F>G C$ is completely similar. We consequently obtain the converse inequalities $K F>L C, K E<L E, D K<B L, D F<A D$, hence $1<\\frac{A D}{D F}=\\frac{G C}{C F} ;$ a contradiction. ", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a fixed triangle, and let $A_{1}, B_{1}, C_{1}$ be the midpoints of sides $B C, C A, A B$, respectively. Let $P$ be a variable point on the circumcircle. Let lines $P A_{1}, P B_{1}, P C_{1}$ meet the circumcircle again at $A^{\\prime}, B^{\\prime}, C^{\\prime}$ respectively. Assume that the points $A, B, C, A^{\\prime}, B^{\\prime}, C^{\\prime}$ are distinct, and lines $A A^{\\prime}, B B^{\\prime}, C C^{\\prime}$ form a triangle. Prove that the area of this triangle does not depend on $P$. (United Kingdom)", "solution": "Let $A_{0}, B_{0}, C_{0}$ be the points of intersection of the lines $A A^{\\prime}, B B^{\\prime}$ and $C C^{\\prime}$ (see Figure). We claim that area $\\left(A_{0} B_{0} C_{0}\\right)=\\frac{1}{2}$ area $(A B C)$, hence it is constant. Consider the inscribed hexagon $A B C C^{\\prime} P A^{\\prime}$. By Pascal's theorem, the points of intersection of its opposite sides (or of their extensions) are collinear. These points are $A B \\cap C^{\\prime} P=C_{1}$, $B C \\cap P A^{\\prime}=A_{1}, C C^{\\prime} \\cap A^{\\prime} A=B_{0}$. So point $B_{0}$ lies on the midline $A_{1} C_{1}$ of triangle $A B C$. Analogously, points $A_{0}$ and $C_{0}$ lie on lines $B_{1} C_{1}$ and $A_{1} B_{1}$, respectively. Lines $A C$ and $A_{1} C_{1}$ are parallel, so triangles $B_{0} C_{0} A_{1}$ and $A C_{0} B_{1}$ are similar; hence we have $$ \\frac{B_{0} C_{0}}{A C_{0}}=\\frac{A_{1} C_{0}}{B_{1} C_{0}} $$ Analogously, from $B C \\| B_{1} C_{1}$ we obtain $$ \\frac{A_{1} C_{0}}{B_{1} C_{0}}=\\frac{B C_{0}}{A_{0} C_{0}} $$ Combining these equalities, we get $$ \\frac{B_{0} C_{0}}{A C_{0}}=\\frac{B C_{0}}{A_{0} C_{0}} $$ or $$ A_{0} C_{0} \\cdot B_{0} C_{0}=A C_{0} \\cdot B C_{0} $$ Hence we have 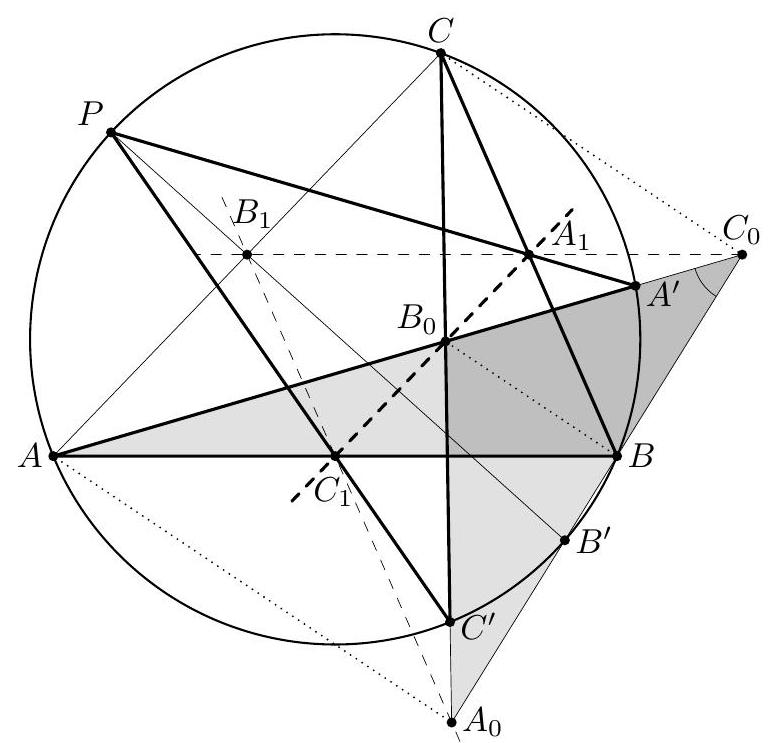 $$ \\operatorname{area}\\left(A_{0} B_{0} C_{0}\\right)=\\frac{1}{2} A_{0} C_{0} \\cdot B_{0} C_{0} \\sin \\angle A_{0} C_{0} B_{0}=\\frac{1}{2} A C_{0} \\cdot B C_{0} \\sin \\angle A C_{0} B=\\operatorname{area}\\left(A B C_{0}\\right) \\text {. } $$ Since $C_{0}$ lies on the midline, we have $d\\left(C_{0}, A B\\right)=\\frac{1}{2} d(C, A B)$ (we denote by $d(X, Y Z)$ the distance between point $X$ and line $Y Z$ ). Then we obtain $$ \\operatorname{area}\\left(A_{0} B_{0} C_{0}\\right)=\\operatorname{area}\\left(A B C_{0}\\right)=\\frac{1}{2} A B \\cdot d\\left(C_{0}, A B\\right)=\\frac{1}{4} A B \\cdot d(C, A B)=\\frac{1}{2} \\operatorname{area}(A B C) . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a fixed triangle, and let $A_{1}, B_{1}, C_{1}$ be the midpoints of sides $B C, C A, A B$, respectively. Let $P$ be a variable point on the circumcircle. Let lines $P A_{1}, P B_{1}, P C_{1}$ meet the circumcircle again at $A^{\\prime}, B^{\\prime}, C^{\\prime}$ respectively. Assume that the points $A, B, C, A^{\\prime}, B^{\\prime}, C^{\\prime}$ are distinct, and lines $A A^{\\prime}, B B^{\\prime}, C C^{\\prime}$ form a triangle. Prove that the area of this triangle does not depend on $P$. (United Kingdom)", "solution": "Again, we prove that $\\operatorname{area}\\left(A_{0} B_{0} C_{0}\\right)=\\frac{1}{2} \\operatorname{area}(A B C)$. We can assume that $P$ lies on arc $A C$. Mark a point $L$ on side $A C$ such that $\\angle C B L=$ $\\angle P B A$; then $\\angle L B A=\\angle C B A-\\angle C B L=\\angle C B A-\\angle P B A=\\angle C B P$. Note also that $\\angle B A L=\\angle B A C=\\angle B P C$ and $\\angle L C B=\\angle A P B$. Hence, triangles $B A L$ and $B P C$ are similar, and so are triangles $L C B$ and $A P B$. Analogously, mark points $K$ and $M$ respectively on the extensions of sides $C B$ and $A B$ beyond point $B$, such that $\\angle K A B=\\angle C A P$ and $\\angle B C M=\\angle P C A$. For analogous reasons, $\\angle K A C=\\angle B A P$ and $\\angle A C M=\\angle P C B$. Hence $\\triangle A B K \\sim \\triangle A P C \\sim \\triangle M B C, \\triangle A C K \\sim$ $\\triangle A P B$, and $\\triangle M A C \\sim \\triangle B P C$. From these similarities, we have $\\angle C M B=\\angle K A B=\\angle C A P$, while we have seen that $\\angle C A P=\\angle C B P=\\angle L B A$. Hence, $A K\\|B L\\| C M$. 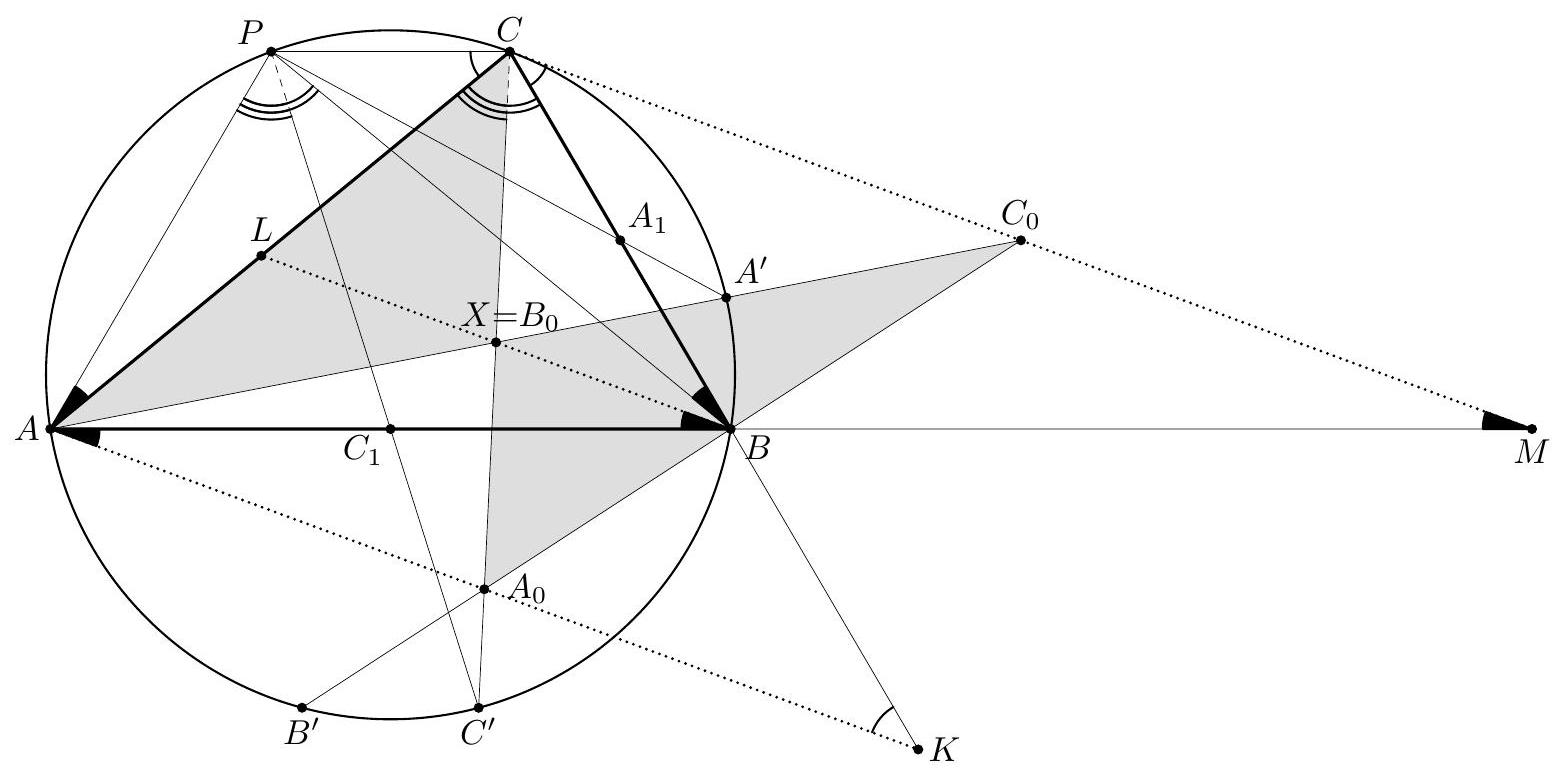 Let line $C C^{\\prime}$ intersect $B L$ at point $X$. Note that $\\angle L C X=\\angle A C C^{\\prime}=\\angle A P C^{\\prime}=\\angle A P C_{1}$, and $P C_{1}$ is a median in triangle $A P B$. Since triangles $A P B$ and $L C B$ are similar, $C X$ is a median in triangle $L C B$, and $X$ is a midpoint of $B L$. For the same reason, $A A^{\\prime}$ passes through this midpoint, so $X=B_{0}$. Analogously, $A_{0}$ and $C_{0}$ are the midpoints of $A K$ and $C M$. Now, from $A A_{0} \\| C C_{0}$, we have $$ \\operatorname{area}\\left(A_{0} B_{0} C_{0}\\right)=\\operatorname{area}\\left(A C_{0} A_{0}\\right)-\\operatorname{area}\\left(A B_{0} A_{0}\\right)=\\operatorname{area}\\left(A C A_{0}\\right)-\\operatorname{area}\\left(A B_{0} A_{0}\\right)=\\operatorname{area}\\left(A C B_{0}\\right) \\text {. } $$ Finally, $$ \\operatorname{area}\\left(A_{0} B_{0} C_{0}\\right)=\\operatorname{area}\\left(A C B_{0}\\right)=\\frac{1}{2} B_{0} L \\cdot A C \\sin A L B_{0}=\\frac{1}{4} B L \\cdot A C \\sin A L B=\\frac{1}{2} \\operatorname{area}(A B C) . $$ Comment 1. The equality area $\\left(A_{0} B_{0} C_{0}\\right)=\\operatorname{area}\\left(A C B_{0}\\right)$ in Solution 2 does not need to be proved since the following fact is frequently known. Suppose that the lines $K L$ and $M N$ are parallel, while the lines $K M$ and $L N$ intersect in a point $E$. Then $\\operatorname{area}(K E N)=\\operatorname{area}(M E L)$. Comment 2. It follows immediately from both solutions that $A A_{0}\\left\\|B B_{0}\\right\\| C C_{0}$. These lines pass through an ideal point which is isogonally conjugate to $P$. It is known that they are parallel to the Simson line of point $Q$ which is opposite to $P$ on the circumcircle. Comment 3. If $A=A^{\\prime}$, then one can define the line $A A^{\\prime}$ to be the tangent to the circumcircle at point $A$. Then the statement of the problem is also valid in this case.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G6", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Determine the smallest positive real number $k$ with the following property. Let $A B C D$ be a convex quadrilateral, and let points $A_{1}, B_{1}, C_{1}$ and $D_{1}$ lie on sides $A B, B C$, $C D$ and $D A$, respectively. Consider the areas of triangles $A A_{1} D_{1}, B B_{1} A_{1}, C C_{1} B_{1}$, and $D D_{1} C_{1}$; let $S$ be the sum of the two smallest ones, and let $S_{1}$ be the area of quadrilateral $A_{1} B_{1} C_{1} D_{1}$. Then we always have $k S_{1} \\geq S$. (U.S.A.) Answer. $k=1$.", "solution": "Throughout the solution, triangles $A A_{1} D_{1}, B B_{1} A_{1}, C C_{1} B_{1}$, and $D D_{1} C_{1}$ will be referred to as border triangles. We will denote by $[\\mathcal{R}]$ the area of a region $\\mathcal{R}$. First, we show that $k \\geq 1$. Consider a triangle $A B C$ with unit area; let $A_{1}, B_{1}, K$ be the midpoints of its sides $A B, B C, A C$, respectively. Choose a point $D$ on the extension of $B K$, close to $K$. Take points $C_{1}$ and $D_{1}$ on sides $C D$ and $D A$ close to $D$ (see Figure 1). We have $\\left[B B_{1} A_{1}\\right]=\\frac{1}{4}$. Moreover, as $C_{1}, D_{1}, D \\rightarrow K$, we get $\\left[A_{1} B_{1} C_{1} D_{1}\\right] \\rightarrow\\left[A_{1} B_{1} K\\right]=\\frac{1}{4}$, $\\left[A A_{1} D_{1}\\right] \\rightarrow\\left[A A_{1} K\\right]=\\frac{1}{4},\\left[C C_{1} B_{1}\\right] \\rightarrow\\left[C K B_{1}\\right]=\\frac{1}{4}$ and $\\left[D D_{1} C_{1}\\right] \\rightarrow 0$. Hence, the sum of the two smallest areas of border triangles tends to $\\frac{1}{4}$, as well as $\\left[A_{1} B_{1} C_{1} D_{1}\\right]$; therefore, their ratio tends to 1 , and $k \\geq 1$. We are left to prove that $k=1$ satisfies the desired property. 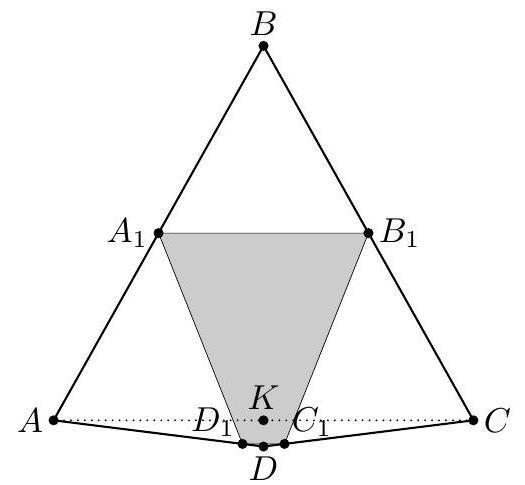 Figure 1 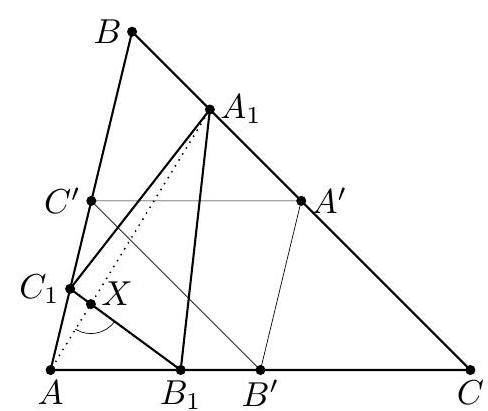 Figure 2  Figure 3 Lemma. Let points $A_{1}, B_{1}, C_{1}$ lie respectively on sides $B C, C A, A B$ of a triangle $A B C$. Then $\\left[A_{1} B_{1} C_{1}\\right] \\geq \\min \\left\\{\\left[A C_{1} B_{1}\\right],\\left[B A_{1} C_{1}\\right],\\left[C B_{1} A_{1}\\right]\\right\\}$. Proof. Let $A^{\\prime}, B^{\\prime}, C^{\\prime}$ be the midpoints of sides $B C, C A$ and $A B$, respectively. Suppose that two of points $A_{1}, B_{1}, C_{1}$ lie in one of triangles $A C^{\\prime} B^{\\prime}, B A^{\\prime} C^{\\prime}$ and $C B^{\\prime} A^{\\prime}$ (for convenience, let points $B_{1}$ and $C_{1}$ lie in triangle $A C^{\\prime} B^{\\prime}$; see Figure 2). Let segments $B_{1} C_{1}$ and $A A_{1}$ intersect at point $X$. Then $X$ also lies in triangle $A C^{\\prime} B^{\\prime}$. Hence $A_{1} X \\geq A X$, and we have $$ \\frac{\\left[A_{1} B_{1} C_{1}\\right]}{\\left[A C_{1} B_{1}\\right]}=\\frac{\\frac{1}{2} A_{1} X \\cdot B_{1} C_{1} \\cdot \\sin \\angle A_{1} X C_{1}}{\\frac{1}{2} A X \\cdot B_{1} C_{1} \\cdot \\sin \\angle A X B_{1}}=\\frac{A_{1} X}{A X} \\geq 1 $$ as required. Otherwise, each one of triangles $A C^{\\prime} B^{\\prime}, B A^{\\prime} C^{\\prime}, C B^{\\prime} A^{\\prime}$ contains exactly one of points $A_{1}$, $B_{1}, C_{1}$, and we can assume that $B A_{1}<B A^{\\prime}, C B_{1}<C B^{\\prime}, A C_{1}<A C^{\\prime}$ (see Figure 3). Then lines $B_{1} A_{1}$ and $A B$ intersect at a point $Y$ on the extension of $A B$ beyond point $B$, hence $\\frac{\\left[A_{1} B_{1} C_{1}\\right]}{\\left[A_{1} B_{1} C^{\\prime}\\right]}=\\frac{C_{1} Y}{C^{\\prime} Y}>1$; also, lines $A_{1} C^{\\prime}$ and $C A$ intersect at a point $Z$ on the extension of $C A$ beyond point $A$, hence $\\frac{\\left[A_{1} B_{1} C^{\\prime}\\right]}{\\left[A_{1} B^{\\prime} C^{\\prime}\\right]}=\\frac{B_{1} Z}{B^{\\prime} Z}>1$. Finally, since $A_{1} A^{\\prime} \\| B^{\\prime} C^{\\prime}$, we have $\\left[A_{1} B_{1} C_{1}\\right]>\\left[A_{1} B_{1} C^{\\prime}\\right]>\\left[A_{1} B^{\\prime} C^{\\prime}\\right]=\\left[A^{\\prime} B^{\\prime} C^{\\prime}\\right]=\\frac{1}{4}[A B C]$. Now, from $\\left[A_{1} B_{1} C_{1}\\right]+\\left[A C_{1} B_{1}\\right]+\\left[B A_{1} C_{1}\\right]+\\left[C B_{1} A_{1}\\right]=[A B C]$ we obtain that one of the remaining triangles $A C_{1} B_{1}, B A_{1} C_{1}, C B_{1} A_{1}$ has an area less than $\\frac{1}{4}[A B C]$, so it is less than $\\left[A_{1} B_{1} C_{1}\\right]$. Now we return to the problem. We say that triangle $A_{1} B_{1} C_{1}$ is small if $\\left[A_{1} B_{1} C_{1}\\right]$ is less than each of $\\left[B B_{1} A_{1}\\right]$ and $\\left[C C_{1} B_{1}\\right]$; otherwise this triangle is big (the similar notion is introduced for triangles $B_{1} C_{1} D_{1}, C_{1} D_{1} A_{1}, D_{1} A_{1} B_{1}$ ). If both triangles $A_{1} B_{1} C_{1}$ and $C_{1} D_{1} A_{1}$ are big, then $\\left[A_{1} B_{1} C_{1}\\right]$ is not less than the area of some border triangle, and $\\left[C_{1} D_{1} A_{1}\\right]$ is not less than the area of another one; hence, $S_{1}=\\left[A_{1} B_{1} C_{1}\\right]+\\left[C_{1} D_{1} A_{1}\\right] \\geq S$. The same is valid for the pair of $B_{1} C_{1} D_{1}$ and $D_{1} A_{1} B_{1}$. So it is sufficient to prove that in one of these pairs both triangles are big. Suppose the contrary. Then there is a small triangle in each pair. Without loss of generality, assume that triangles $A_{1} B_{1} C_{1}$ and $D_{1} A_{1} B_{1}$ are small. We can assume also that $\\left[A_{1} B_{1} C_{1}\\right] \\leq$ $\\left[D_{1} A_{1} B_{1}\\right]$. Note that in this case ray $D_{1} C_{1}$ intersects line $B C$. Consider two cases.  Figure 4  Figure 5 Case 1. Ray $C_{1} D_{1}$ intersects line $A B$ at some point $K$. Let ray $D_{1} C_{1}$ intersect line $B C$ at point $L$ (see Figure 4). Then we have $\\left[A_{1} B_{1} C_{1}\\right]<\\left[C C_{1} B_{1}\\right]<\\left[L C_{1} B_{1}\\right],\\left[A_{1} B_{1} C_{1}\\right]<\\left[B B_{1} A_{1}\\right]$ (both - since $\\left[A_{1} B_{1} C_{1}\\right]$ is small), and $\\left[A_{1} B_{1} C_{1}\\right] \\leq\\left[D_{1} A_{1} B_{1}\\right]<\\left[A A_{1} D_{1}\\right]<\\left[K A_{1} D_{1}\\right]<\\left[K A_{1} C_{1}\\right]$ (since triangle $D_{1} A_{1} B_{1}$ is small). This contradicts the Lemma, applied for triangle $A_{1} B_{1} C_{1}$ inside $L K B$. Case 2. Ray $C_{1} D_{1}$ does not intersect $A B$. Then choose a \"sufficiently far\" point $K$ on ray $B A$ such that $\\left[K A_{1} C_{1}\\right]>\\left[A_{1} B_{1} C_{1}\\right]$, and that ray $K C_{1}$ intersects line $B C$ at some point $L$ (see Figure 5). Since ray $C_{1} D_{1}$ does not intersect line $A B$, the points $A$ and $D_{1}$ are on different sides of $K L$; then $A$ and $D$ are also on different sides, and $C$ is on the same side as $A$ and $B$. Then analogously we have $\\left[A_{1} B_{1} C_{1}\\right]<\\left[C C_{1} B_{1}\\right]<\\left[L C_{1} B_{1}\\right]$ and $\\left[A_{1} B_{1} C_{1}\\right]<\\left[B B_{1} A_{1}\\right]$ since triangle $A_{1} B_{1} C_{1}$ is small. This (together with $\\left[A_{1} B_{1} C_{1}\\right]<\\left[K A_{1} C_{1}\\right]$ ) contradicts the Lemma again.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G7", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Given an acute triangle $A B C$ with angles $\\alpha, \\beta$ and $\\gamma$ at vertices $A, B$ and $C$, respectively, such that $\\beta>\\gamma$. Point $I$ is the incenter, and $R$ is the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $A D$ such that $A K=2 R$, and $D$ separates $A$ and $K$. Finally, lines $D I$ and $K I$ meet sides $A C$ and $B C$ at $E$ and $F$, respectively. Prove that if $I E=I F$ then $\\beta \\leq 3 \\gamma$. (Iran)", "solution": "We first prove that $$ \\angle K I D=\\frac{\\beta-\\gamma}{2} $$ even without the assumption that $I E=I F$. Then we will show that the statement of the problem is a consequence of this fact. Denote the circumcenter by $O$. On the circumcircle, let $P$ be the point opposite to $A$, and let the angle bisector $A I$ intersect the circle again at $M$. Since $A K=A P=2 R$, triangle $A K P$ is isosceles. It is known that $\\angle B A D=\\angle C A O$, hence $\\angle D A I=\\angle B A I-\\angle B A D=\\angle C A I-$ $\\angle C A O=\\angle O A I$, and $A M$ is the bisector line in triangle $A K P$. Therefore, points $K$ and $P$ are symmetrical about $A M$, and $\\angle A M K=\\angle A M P=90^{\\circ}$. Thus, $M$ is the midpoint of $K P$, and $A M$ is the perpendicular bisector of $K P$.  Denote the perpendicular feet of incenter $I$ on lines $B C, A C$, and $A D$ by $A_{1}, B_{1}$, and $T$, respectively. Quadrilateral $D A_{1} I T$ is a rectangle, hence $T D=I A_{1}=I B_{1}$. Due to the right angles at $T$ and $B_{1}$, quadrilateral $A B_{1} I T$ is cyclic. Hence $\\angle B_{1} T I=$ $\\angle B_{1} A I=\\angle C A M=\\angle B A M=\\angle B P M$ and $\\angle I B_{1} T=\\angle I A T=\\angle M A K=\\angle M A P=$ $\\angle M B P$. Therefore, triangles $B_{1} T I$ and $B P M$ are similar and $\\frac{I T}{I B_{1}}=\\frac{M P}{M B}$. It is well-known that $M B=M C=M I$. Then right triangles $I T D$ and $K M I$ are also similar, because $\\frac{I T}{T D}=\\frac{I T}{I B_{1}}=\\frac{M P}{M B}=\\frac{K M}{M I}$. Hence, $\\angle K I M=\\angle I D T=\\angle I D A$, and $$ \\angle K I D=\\angle M I D-\\angle K I M=(\\angle I A D+\\angle I D A)-\\angle I D A=\\angle I A D . $$ Finally, from the right triangle $A D B$ we can compute $$ \\angle K I D=\\angle I A D=\\angle I A B-\\angle D A B=\\frac{\\alpha}{2}-\\left(90^{\\circ}-\\beta\\right)=\\frac{\\alpha}{2}-\\frac{\\alpha+\\beta+\\gamma}{2}+\\beta=\\frac{\\beta-\\gamma}{2} . $$ Now let us turn to the statement and suppose that $I E=I F$. Since $I A_{1}=I B_{1}$, the right triangles $I E B_{1}$ and $I F A_{1}$ are congruent and $\\angle I E B_{1}=\\angle I F A_{1}$. Since $\\beta>\\gamma, A_{1}$ lies in the interior of segment $C D$ and $F$ lies in the interior of $A_{1} D$. Hence, $\\angle I F C$ is acute. Then two cases are possible depending on the order of points $A, C, B_{1}$ and $E$.  If point $E$ lies between $C$ and $B_{1}$ then $\\angle I F C=\\angle I E A$, hence quadrilateral $C E I F$ is cyclic and $\\angle F C E=180^{\\circ}-\\angle E I F=\\angle K I D$. By (1), in this case we obtain $\\angle F C E=\\gamma=\\angle K I D=$ $\\frac{\\beta-\\gamma}{2}$ and $\\beta=3 \\gamma$. Otherwise, if point $E$ lies between $A$ and $B_{1}$, quadrilateral $C E I F$ is a deltoid such that $\\angle I E C=\\angle I F C<90^{\\circ}$. Then we have $\\angle F C E>180^{\\circ}-\\angle E I F=\\angle K I D$. Therefore, $\\angle F C E=\\gamma>\\angle K I D=\\frac{\\beta-\\gamma}{2}$ and $\\beta<3 \\gamma$. Comment 1. In the case when quadrilateral $C E I F$ is a deltoid, one can prove the desired inequality without using (1). Actually, from $\\angle I E C=\\angle I F C<90^{\\circ}$ it follows that $\\angle A D I=90^{\\circ}-\\angle E D C<$ $\\angle A E D-\\angle E D C=\\gamma$. Since the incircle lies inside triangle $A B C$, we have $A D>2 r$ (here $r$ is the inradius), which implies $D T<T A$ and $D I<A I$; hence $\\frac{\\beta-\\gamma}{2}=\\angle I A D<\\angle A D I<\\gamma$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G7", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Given an acute triangle $A B C$ with angles $\\alpha, \\beta$ and $\\gamma$ at vertices $A, B$ and $C$, respectively, such that $\\beta>\\gamma$. Point $I$ is the incenter, and $R$ is the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $A D$ such that $A K=2 R$, and $D$ separates $A$ and $K$. Finally, lines $D I$ and $K I$ meet sides $A C$ and $B C$ at $E$ and $F$, respectively. Prove that if $I E=I F$ then $\\beta \\leq 3 \\gamma$. (Iran)", "solution": "We give a different proof for (1). Then the solution can be finished in the same way as above. Define points $M$ and $P$ again; it can be proved in the same way that $A M$ is the perpendicular bisector of $K P$. Let $J$ be the center of the excircle touching side $B C$. It is well-known that points $B, C, I, J$ lie on a circle with center $M$; denote this circle by $\\omega_{1}$. Let $B^{\\prime}$ be the reflection of point $B$ about the angle bisector $A M$. By the symmetry, $B^{\\prime}$ is the second intersection point of circle $\\omega_{1}$ and line $A C$. Triangles $P B A$ and $K B^{\\prime} A$ are symmetrical with respect to line $A M$, therefore $\\angle K B^{\\prime} A=\\angle P B A=90^{\\circ}$. By the right angles at $D$ and $B^{\\prime}$, points $K, D, B^{\\prime}, C$ are concyclic and $$ A D \\cdot A K=A B^{\\prime} \\cdot A C . $$ From the cyclic quadrilateral $I J C B^{\\prime}$ we obtain $A B^{\\prime} \\cdot A C=A I \\cdot A J$ as well, therefore $$ A D \\cdot A K=A B^{\\prime} \\cdot A C=A I \\cdot A J $$ and points $I, J, K, D$ are also concyclic. Denote circle $I D K J$ by $\\omega_{2}$.  Let $N$ be the point on circle $\\omega_{2}$ which is opposite to $K$. Since $\\angle N D K=90^{\\circ}=\\angle C D K$, point $N$ lies on line $B C$. Point $M$, being the center of circle $\\omega_{1}$, is the midpoint of segment $I J$, and $K M$ is perpendicular to $I J$. Therefore, line $K M$ is the perpendicular bisector of $I J$ and hence it passes through $N$. From the cyclic quadrilateral $I D K N$ we obtain $$ \\angle K I D=\\angle K N D=90^{\\circ}-\\angle D K N=90^{\\circ}-\\angle A K M=\\angle M A K=\\frac{\\beta-\\gamma}{2} $$ Comment 2. The main difficulty in the solution is finding (1). If someone can guess this fact, he or she can compute it in a relatively short way. One possible way is finding and applying the relation $A I^{2}=2 R\\left(h_{a}-2 r\\right)$, where $h_{a}=A D$ is the length of the altitude. Using this fact, one can see that triangles $A K I$ and $A I D^{\\prime}$ are similar (here $D^{\\prime}$ is the point symmetrical to $D$ about $T$ ). Hence, $\\angle M I K=\\angle D D^{\\prime} I=\\angle I D D^{\\prime}$. The proof can be finished as in Solution 1.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "G8", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Point $P$ lies on side $A B$ of a convex quadrilateral $A B C D$. Let $\\omega$ be the incircle of triangle $C P D$, and let $I$ be its incenter. Suppose that $\\omega$ is tangent to the incircles of triangles $A P D$ and $B P C$ at points $K$ and $L$, respectively. Let lines $A C$ and $B D$ meet at $E$, and let lines $A K$ and $B L$ meet at $F$. Prove that points $E, I$, and $F$ are collinear. (Poland)", "solution": "Let $\\Omega$ be the circle tangent to segment $A B$ and to rays $A D$ and $B C$; let $J$ be its center. We prove that points $E$ and $F$ lie on line $I J$.  Denote the incircles of triangles $A D P$ and $B C P$ by $\\omega_{A}$ and $\\omega_{B}$. Let $h_{1}$ be the homothety with a negative scale taking $\\omega$ to $\\Omega$. Consider this homothety as the composition of two homotheties: one taking $\\omega$ to $\\omega_{A}$ (with a negative scale and center $K$ ), and another one taking $\\omega_{A}$ to $\\Omega$ (with a positive scale and center $A$ ). It is known that in such a case the three centers of homothety are collinear (this theorem is also referred to as the theorem on the three similitude centers). Hence, the center of $h_{1}$ lies on line $A K$. Analogously, it also lies on $B L$, so this center is $F$. Hence, $F$ lies on the line of centers of $\\omega$ and $\\Omega$, i. e. on $I J$ (if $I=J$, then $F=I$ as well, and the claim is obvious). Consider quadrilateral $A P C D$ and mark the equal segments of tangents to $\\omega$ and $\\omega_{A}$ (see the figure below to the left). Since circles $\\omega$ and $\\omega_{A}$ have a common point of tangency with $P D$, one can easily see that $A D+P C=A P+C D$. So, quadrilateral $A P C D$ is circumscribed; analogously, circumscribed is also quadrilateral $B C D P$. Let $\\Omega_{A}$ and $\\Omega_{B}$ respectively be their incircles.  Consider the homothety $h_{2}$ with a positive scale taking $\\omega$ to $\\Omega$. Consider $h_{2}$ as the composition of two homotheties: taking $\\omega$ to $\\Omega_{A}$ (with a positive scale and center $C$ ), and taking $\\Omega_{A}$ to $\\Omega$ (with a positive scale and center $A$ ), respectively. So the center of $h_{2}$ lies on line $A C$. By analogous reasons, it lies also on $B D$, hence this center is $E$. Thus, $E$ also lies on the line of centers $I J$, and the claim is proved. Comment. In both main steps of the solution, there can be several different reasonings for the same claims. For instance, one can mostly use Desargues' theorem instead of the three homotheties theorem. Namely, if $I_{A}$ and $I_{B}$ are the centers of $\\omega_{A}$ and $\\omega_{B}$, then lines $I_{A} I_{B}, K L$ and $A B$ are concurrent (by the theorem on three similitude centers applied to $\\omega, \\omega_{A}$ and $\\omega_{B}$ ). Then Desargues' theorem, applied to triangles $A I_{A} K$ and $B I_{B} L$, yields that the points $J=A I_{A} \\cap B I_{B}, I=I_{A} K \\cap I_{B} L$ and $F=A K \\cap B L$ are collinear. For the second step, let $J_{A}$ and $J_{B}$ be the centers of $\\Omega_{A}$ and $\\Omega_{B}$. Then lines $J_{A} J_{B}, A B$ and $C D$ are concurrent, since they appear to be the two common tangents and the line of centers of $\\Omega_{A}$ and $\\Omega_{B}$. Applying Desargues' theorem to triangles $A J_{A} C$ and $B J_{B} D$, we obtain that the points $J=A J_{A} \\cap B J_{B}$, $I=C J_{A} \\cap D J_{B}$ and $E=A C \\cap B D$ are collinear.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N1", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Find all pairs $(k, n)$ of positive integers for which $7^{k}-3^{n}$ divides $k^{4}+n^{2}$. (Austria) Answer. $(2,4)$.", "solution": "Suppose that a pair $(k, n)$ satisfies the condition of the problem. Since $7^{k}-3^{n}$ is even, $k^{4}+n^{2}$ is also even, hence $k$ and $n$ have the same parity. If $k$ and $n$ are odd, then $k^{4}+n^{2} \\equiv 1+1=2(\\bmod 4)$, while $7^{k}-3^{n} \\equiv 7-3 \\equiv 0(\\bmod 4)$, so $k^{4}+n^{2}$ cannot be divisible by $7^{k}-3^{n}$. Hence, both $k$ and $n$ must be even. Write $k=2 a, n=2 b$. Then $7^{k}-3^{n}=7^{2 a}-3^{2 b}=\\frac{7^{a}-3^{b}}{2} \\cdot 2\\left(7^{a}+3^{b}\\right)$, and both factors are integers. So $2\\left(7^{a}+3^{b}\\right) \\mid 7^{k}-3^{n}$ and $7^{k}-3^{n} \\mid k^{4}+n^{2}=2\\left(8 a^{4}+2 b^{2}\\right)$, hence $$ 7^{a}+3^{b} \\leq 8 a^{4}+2 b^{2} . $$ We prove by induction that $8 a^{4}<7^{a}$ for $a \\geq 4,2 b^{2}<3^{b}$ for $b \\geq 1$ and $2 b^{2}+9 \\leq 3^{b}$ for $b \\geq 3$. In the initial cases $a=4, b=1, b=2$ and $b=3$ we have $8 \\cdot 4^{4}=2048<7^{4}=2401,2<3$, $2 \\cdot 2^{2}=8<3^{2}=9$ and $2 \\cdot 3^{2}+9=3^{3}=27$, respectively. If $8 a^{4}<7^{a}(a \\geq 4)$ and $2 b^{2}+9 \\leq 3^{b}(b \\geq 3)$, then $$ \\begin{aligned} 8(a+1)^{4} & =8 a^{4}\\left(\\frac{a+1}{a}\\right)^{4}<7^{a}\\left(\\frac{5}{4}\\right)^{4}=7^{a} \\frac{625}{256}<7^{a+1} \\quad \\text { and } \\\\ 2(b+1)^{2}+9 & <\\left(2 b^{2}+9\\right)\\left(\\frac{b+1}{b}\\right)^{2} \\leq 3^{b}\\left(\\frac{4}{3}\\right)^{2}=3^{b} \\frac{16}{9}<3^{b+1}, \\end{aligned} $$ as desired. For $a \\geq 4$ we obtain $7^{a}+3^{b}>8 a^{4}+2 b^{2}$ and inequality (1) cannot hold. Hence $a \\leq 3$, and three cases are possible. Case 1: $a=1$. Then $k=2$ and $8+2 b^{2} \\geq 7+3^{b}$, thus $2 b^{2}+1 \\geq 3^{b}$. This is possible only if $b \\leq 2$. If $b=1$ then $n=2$ and $\\frac{k^{4}+n^{2}}{7^{k}-3^{n}}=\\frac{2^{4}+2^{2}}{7^{2}-3^{2}}=\\frac{1}{2}$, which is not an integer. If $b=2$ then $n=4$ and $\\frac{k^{4}+n^{2}}{7^{k}-3^{n}}=\\frac{2^{4}+4^{2}}{7^{2}-3^{4}}=-1$, so $(k, n)=(2,4)$ is a solution. Case 2: $a=2$. Then $k=4$ and $k^{4}+n^{2}=256+4 b^{2} \\geq\\left|7^{4}-3^{n}\\right|=\\left|49-3^{b}\\right| \\cdot\\left(49+3^{b}\\right)$. The smallest value of the first factor is 22 , attained at $b=3$, so $128+2 b^{2} \\geq 11\\left(49+3^{b}\\right)$, which is impossible since $3^{b}>2 b^{2}$. Case 3: $a=3$. Then $k=6$ and $k^{4}+n^{2}=1296+4 b^{2} \\geq\\left|7^{6}-3^{n}\\right|=\\left|343-3^{b}\\right| \\cdot\\left(343+3^{b}\\right)$. Analogously, $\\left|343-3^{b}\\right| \\geq 100$ and we have $324+b^{2} \\geq 25\\left(343+3^{b}\\right)$, which is impossible again. We find that there exists a unique solution $(k, n)=(2,4)$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N2", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $b, n>1$ be integers. Suppose that for each $k>1$ there exists an integer $a_{k}$ such that $b-a_{k}^{n}$ is divisible by $k$. Prove that $b=A^{n}$ for some integer $A$. (Canada)", "solution": "Let the prime factorization of $b$ be $b=p_{1}^{\\alpha_{1}} \\ldots p_{s}^{\\alpha_{s}}$, where $p_{1}, \\ldots, p_{s}$ are distinct primes. Our goal is to show that all exponents $\\alpha_{i}$ are divisible by $n$, then we can set $A=p_{1}^{\\alpha_{1} / n} \\ldots p_{s}^{\\alpha_{s} / n}$. Apply the condition for $k=b^{2}$. The number $b-a_{k}^{n}$ is divisible by $b^{2}$ and hence, for each $1 \\leq i \\leq s$, it is divisible by $p_{i}^{2 \\alpha_{i}}>p_{i}^{\\alpha_{i}}$ as well. Therefore $$ a_{k}^{n} \\equiv b \\equiv 0 \\quad\\left(\\bmod p_{i}^{\\alpha_{i}}\\right) $$ and $$ a_{k}^{n} \\equiv b \\not \\equiv 0 \\quad\\left(\\bmod p_{i}^{\\alpha_{i}+1}\\right) $$ which implies that the largest power of $p_{i}$ dividing $a_{k}^{n}$ is $p_{i}^{\\alpha_{i}}$. Since $a_{k}^{n}$ is a complete $n$th power, this implies that $\\alpha_{i}$ is divisible by $n$. Comment. If $n=8$ and $b=16$, then for each prime $p$ there exists an integer $a_{p}$ such that $b-a_{p}^{n}$ is divisible by $p$. Actually, the congruency $x^{8}-16 \\equiv 0(\\bmod p)$ expands as $$ \\left(x^{2}-2\\right)\\left(x^{2}+2\\right)\\left(x^{2}-2 x+2\\right)\\left(x^{2}+2 x+2\\right) \\equiv 0 \\quad(\\bmod p) $$ Hence, if -1 is a quadratic residue modulo $p$, then congruency $x^{2}+2 x+2=(x+1)^{2}+1 \\equiv 0$ has a solution. Otherwise, one of congruencies $x^{2} \\equiv 2$ and $x^{2} \\equiv-2$ has a solution. Thus, the solution cannot work using only prime values of $k$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N3", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $X$ be a set of 10000 integers, none of them is divisible by 47 . Prove that there exists a 2007-element subset $Y$ of $X$ such that $a-b+c-d+e$ is not divisible by 47 for any $a, b, c, d, e \\in Y$. (Netherlands)", "solution": "Call a set $M$ of integers good if $47 \\nmid a-b+c-d+e$ for any $a, b, c, d, e \\in M$. Consider the set $J=\\{-9,-7,-5,-3,-1,1,3,5,7,9\\}$. We claim that $J$ is good. Actually, for any $a, b, c, d, e \\in J$ the number $a-b+c-d+e$ is odd and $$ -45=(-9)-9+(-9)-9+(-9) \\leq a-b+c-d+e \\leq 9-(-9)+9-(-9)+9=45 $$ But there is no odd number divisible by 47 between -45 and 45 . For any $k=1, \\ldots, 46$ consider the set $$ A_{k}=\\{x \\in X \\mid \\exists j \\in J: \\quad k x \\equiv j(\\bmod 47)\\} . $$ If $A_{k}$ is not good, then $47 \\mid a-b+c-d+e$ for some $a, b, c, d, e \\in A_{k}$, hence $47 \\mid k a-k b+$ $k c-k d+k e$. But set $J$ contains numbers with the same residues modulo 47 , so $J$ also is not good. This is a contradiction; therefore each $A_{k}$ is a good subset of $X$. Then it suffices to prove that there exists a number $k$ such that $\\left|A_{k}\\right| \\geq 2007$. Note that each $x \\in X$ is contained in exactly 10 sets $A_{k}$. Then $$ \\sum_{k=1}^{46}\\left|A_{k}\\right|=10|X|=100000 $$ hence for some value of $k$ we have $$ \\left|A_{k}\\right| \\geq \\frac{100000}{46}>2173>2007 . $$ This completes the proof. Comment. For the solution, it is essential to find a good set consisting of 10 different residues. Actually, consider a set $X$ containing almost uniform distribution of the nonzero residues (i. e. each residue occurs 217 or 218 times). Let $Y \\subset X$ be a good subset containing 2007 elements. Then the set $K$ of all residues appearing in $Y$ contains not less than 10 residues, and obviously this set is good. On the other hand, there is no good set $K$ consisting of 11 different residues. The CauchyDavenport theorem claims that for any sets $A, B$ of residues modulo a prime $p$, $$ |A+B| \\geq \\min \\{p,|A|+|B|-1\\} . $$ Hence, if $|K| \\geq 11$, then $|K+K| \\geq 21,|K+K+K| \\geq 31>47-|K+K|$, hence $\\mid K+K+K+$ $(-K)+(-K) \\mid=47$, and $0 \\equiv a+c+e-b-d(\\bmod 47)$ for some $a, b, c, d, e \\in K$. From the same reasoning, one can see that a good set $K$ containing 10 residues should satisfy equalities $|K+K|=19=2|K|-1$ and $|K+K+K|=28=|K+K|+|K|-1$. It can be proved that in this case set $K$ consists of 10 residues forming an arithmetic progression. As an easy consequence, one obtains that set $K$ has the form $a J$ for some nonzero residue $a$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N4", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "For every integer $k \\geq 2$, prove that $2^{3 k}$ divides the number $$ \\left(\\begin{array}{c} 2^{k+1} \\\\ 2^{k} \\end{array}\\right)-\\left(\\begin{array}{c} 2^{k} \\\\ 2^{k-1} \\end{array}\\right) $$ but $2^{3 k+1}$ does not. (Poland)", "solution": "We use the notation $(2 n-1) ! !=1 \\cdot 3 \\cdots(2 n-1)$ and $(2 n) ! !=2 \\cdot 4 \\cdots(2 n)=2^{n} n$ ! for any positive integer $n$. Observe that $(2 n) !=(2 n) ! !(2 n-1) ! !=2^{n} n !(2 n-1) !$ !. For any positive integer $n$ we have $$ \\begin{aligned} & \\left(\\begin{array}{l} 4 n \\\\ 2 n \\end{array}\\right)=\\frac{(4 n) !}{(2 n) !^{2}}=\\frac{2^{2 n}(2 n) !(4 n-1) ! !}{(2 n) !^{2}}=\\frac{2^{2 n}}{(2 n) !}(4 n-1) ! ! \\\\ & \\left(\\begin{array}{c} 2 n \\\\ n \\end{array}\\right)=\\frac{1}{(2 n) !}\\left(\\frac{(2 n) !}{n !}\\right)^{2}=\\frac{1}{(2 n) !}\\left(2^{n}(2 n-1) ! !\\right)^{2}=\\frac{2^{2 n}}{(2 n) !}(2 n-1) ! !^{2} . \\end{aligned} $$ Then expression (1) can be rewritten as follows: $$ \\begin{aligned} \\left(\\begin{array}{c} 2^{k+1} \\\\ 2^{k} \\end{array}\\right) & -\\left(\\begin{array}{c} 2^{k} \\\\ 2^{k-1} \\end{array}\\right)=\\frac{2^{2^{k}}}{\\left(2^{k}\\right) !}\\left(2^{k+1}-1\\right) ! !-\\frac{2^{2^{k}}}{\\left(2^{k}\\right) !}\\left(2^{k}-1\\right) ! !^{2} \\\\ & =\\frac{2^{2^{k}}\\left(2^{k}-1\\right) ! !}{\\left(2^{k}\\right) !} \\cdot\\left(\\left(2^{k}+1\\right)\\left(2^{k}+3\\right) \\ldots\\left(2^{k}+2^{k}-1\\right)-\\left(2^{k}-1\\right)\\left(2^{k}-3\\right) \\ldots\\left(2^{k}-2^{k}+1\\right)\\right) . \\end{aligned} $$ We compute the exponent of 2 in the prime decomposition of each factor (the first one is a rational number but not necessarily an integer; it is not important). First, we show by induction on $n$ that the exponent of 2 in $\\left(2^{n}\\right)$ ! is $2^{n}-1$. The base case $n=1$ is trivial. Suppose that $\\left(2^{n}\\right) !=2^{2^{n}-1}(2 d+1)$ for some integer $d$. Then we have $$ \\left(2^{n+1}\\right) !=2^{2^{n}}\\left(2^{n}\\right) !\\left(2^{n+1}-1\\right) ! !=2^{2^{n}} 2^{2^{n}-1} \\cdot(2 d+1)\\left(2^{n+1}-1\\right) ! !=2^{2^{n+1}-1} \\cdot(2 q+1) $$ for some integer $q$. This finishes the induction step. Hence, the exponent of 2 in the first factor in $(2)$ is $2^{k}-\\left(2^{k}-1\\right)=1$. The second factor in (2) can be considered as the value of the polynomial $$ P(x)=(x+1)(x+3) \\ldots\\left(x+2^{k}-1\\right)-(x-1)(x-3) \\ldots\\left(x-2^{k}+1\\right) . $$ at $x=2^{k}$. Now we collect some information about $P(x)$. Observe that $P(-x)=-P(x)$, since $k \\geq 2$. So $P(x)$ is an odd function, and it has nonzero coefficients only at odd powers of $x$. Hence $P(x)=x^{3} Q(x)+c x$, where $Q(x)$ is a polynomial with integer coefficients. Compute the exponent of 2 in $c$. We have $$ \\begin{aligned} c & =2\\left(2^{k}-1\\right) ! ! \\sum_{i=1}^{2^{k-1}} \\frac{1}{2 i-1}=\\left(2^{k}-1\\right) ! ! \\sum_{i=1}^{2^{k-1}}\\left(\\frac{1}{2 i-1}+\\frac{1}{2^{k}-2 i+1}\\right) \\\\ & =\\left(2^{k}-1\\right) ! ! \\sum_{i=1}^{2^{k-1}} \\frac{2^{k}}{(2 i-1)\\left(2^{k}-2 i+1\\right)}=2^{k} \\sum_{i=1}^{2^{k-1}} \\frac{\\left(2^{k}-1\\right) ! !}{(2 i-1)\\left(2^{k}-2 i+1\\right)}=2^{k} S \\end{aligned} $$ For any integer $i=1, \\ldots, 2^{k-1}$, denote by $a_{2 i-1}$ the residue inverse to $2 i-1$ modulo $2^{k}$. Clearly, when $2 i-1$ runs through all odd residues, so does $a_{2 i-1}$, hence $$ \\begin{aligned} & S=\\sum_{i=1}^{2^{k-1}} \\frac{\\left(2^{k}-1\\right) ! !}{(2 i-1)\\left(2^{k}-2 i+1\\right)} \\equiv-\\sum_{i=1}^{2^{k-1}} \\frac{\\left(2^{k}-1\\right) ! !}{(2 i-1)^{2}} \\equiv-\\sum_{i=1}^{2^{k-1}}\\left(2^{k}-1\\right) ! ! a_{2 i-1}^{2} \\\\ &=-\\left(2^{k}-1\\right) ! ! \\sum_{i=1}^{2^{k-1}}(2 i-1)^{2}=-\\left(2^{k}-1\\right) ! ! \\frac{2^{k-1}\\left(2^{2 k}-1\\right)}{3} \\quad\\left(\\bmod 2^{k}\\right) . \\end{aligned} $$ Therefore, the exponent of 2 in $S$ is $k-1$, so $c=2^{k} S=2^{2 k-1}(2 t+1)$ for some integer $t$. Finally we obtain that $$ P\\left(2^{k}\\right)=2^{3 k} Q\\left(2^{k}\\right)+2^{k} c=2^{3 k} Q\\left(2^{k}\\right)+2^{3 k-1}(2 t+1), $$ which is divisible exactly by $2^{3 k-1}$. Thus, the exponent of 2 in $(2)$ is $1+(3 k-1)=3 k$. Comment. The fact that (1) is divisible by $2^{2 k}$ is known; but it does not help in solving this problem.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N5", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Find all surjective functions $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ such that for every $m, n \\in \\mathbb{N}$ and every prime $p$, the number $f(m+n)$ is divisible by $p$ if and only if $f(m)+f(n)$ is divisible by $p$. ( $\\mathbb{N}$ is the set of all positive integers.) (Iran) Answer. $f(n)=n$.", "solution": "Suppose that function $f: \\mathbb{N} \\rightarrow \\mathbb{N}$ satisfies the problem conditions. Lemma. For any prime $p$ and any $x, y \\in \\mathbb{N}$, we have $x \\equiv y(\\bmod p)$ if and only if $f(x) \\equiv f(y)$ $(\\bmod p)$. Moreover, $p \\mid f(x)$ if and only if $p \\mid x$. Proof. Consider an arbitrary prime $p$. Since $f$ is surjective, there exists some $x \\in \\mathbb{N}$ such that $p \\mid f(x)$. Let $$ d=\\min \\{x \\in \\mathbb{N}: p \\mid f(x)\\} . $$ By induction on $k$, we obtain that $p \\mid f(k d)$ for all $k \\in \\mathbb{N}$. The base is true since $p \\mid f(d)$. Moreover, if $p \\mid f(k d)$ and $p \\mid f(d)$ then, by the problem condition, $p \\mid f(k d+d)=f((k+1) d)$ as required. Suppose that there exists an $x \\in \\mathbb{N}$ such that $d \\not x$ but $p \\mid f(x)$. Let $$ y=\\min \\{x \\in \\mathbb{N}: d \\not\\{x, p \\mid f(x)\\} . $$ By the choice of $d$, we have $y>d$, and $y-d$ is a positive integer not divisible by $d$. Then $p \\nmid\\{(y-d)$, while $p \\mid f(d)$ and $p \\mid f(d+(y-d))=f(y)$. This contradicts the problem condition. Hence, there is no such $x$, and $$ p|f(x) \\Longleftrightarrow d| x . $$ Take arbitrary $x, y \\in \\mathbb{N}$ such that $x \\equiv y(\\bmod d)$. We have $p \\mid f(x+(2 x d-x))=f(2 x d)$; moreover, since $d \\mid 2 x d+(y-x)=y+(2 x d-x)$, we get $p \\mid f(y+(2 x d-x))$. Then by the problem condition $p|f(x)+f(2 x d-x), p| f(y)+f(2 x d-x)$, and hence $f(x) \\equiv-f(2 x d-x) \\equiv f(y)$ $(\\bmod p)$. On the other hand, assume that $f(x) \\equiv f(y)(\\bmod p)$. Again we have $p \\mid f(x)+f(2 x d-x)$ which by our assumption implies that $p \\mid f(x)+f(2 x d-x)+(f(y)-f(x))=f(y)+f(2 x d-x)$. Hence by the problem condition $p \\mid f(y+(2 x d-x))$. Using (1) we get $0 \\equiv y+(2 x d-x) \\equiv y-x$ $(\\bmod d)$. Thus, we have proved that $$ x \\equiv y \\quad(\\bmod d) \\Longleftrightarrow f(x) \\equiv f(y) \\quad(\\bmod p) $$ We are left to show that $p=d$ : in this case (1) and (2) provide the desired statements. The numbers $1,2, \\ldots, d$ have distinct residues modulo $d$. By (2), numbers $f(1), f(2), \\ldots$, $f(d)$ have distinct residues modulo $p$; hence there are at least $d$ distinct residues, and $p \\geq d$. On the other hand, by the surjectivity of $f$, there exist $x_{1}, \\ldots, x_{p} \\in \\mathbb{N}$ such that $f\\left(x_{i}\\right)=i$ for any $i=1,2, \\ldots, p$. By (2), all these $x_{i}$ 's have distinct residues modulo $d$. For the same reasons, $d \\geq p$. Hence, $d=p$. Now we prove that $f(n)=n$ by induction on $n$. If $n=1$ then, by the Lemma, $p \\not \\nmid f(1)$ for any prime $p$, so $f(1)=1$, and the base is established. Suppose that $n>1$ and denote $k=f(n)$. Note that there exists a prime $q \\mid n$, so by the Lemma $q \\mid k$ and $k>1$. If $k>n$ then $k-n+1>1$, and there exists a prime $p \\mid k-n+1$; we have $k \\equiv n-1$ $(\\bmod p)$. By the induction hypothesis we have $f(n-1)=n-1 \\equiv k=f(n)(\\bmod p)$. Now, by the Lemma we obtain $n-1 \\equiv n(\\bmod p)$ which cannot be true. Analogously, if $k<n$, then $f(k-1)=k-1$ by induction hypothesis. Moreover, $n-k+1>1$, so there exists a prime $p \\mid n-k+1$ and $n \\equiv k-1(\\bmod p)$. By the Lemma again, $k=f(n) \\equiv$ $f(k-1)=k-1(\\bmod p)$, which is also false. The only remaining case is $k=n$, so $f(n)=n$. Finally, the function $f(n)=n$ obviously satisfies the condition.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N6", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $k$ be a positive integer. Prove that the number $\\left(4 k^{2}-1\\right)^{2}$ has a positive divisor of the form $8 k n-1$ if and only if $k$ is even. (United Kingdom)", "solution": "The statement follows from the following fact. Lemma. For arbitrary positive integers $x$ and $y$, the number $4 x y-1$ divides $\\left(4 x^{2}-1\\right)^{2}$ if and only if $x=y$. Proof. If $x=y$ then $4 x y-1=4 x^{2}-1$ obviously divides $\\left(4 x^{2}-1\\right)^{2}$ so it is sufficient to consider the opposite direction. Call a pair $(x, y)$ of positive integers bad if $4 x y-1$ divides $\\left(4 x^{2}-1\\right)^{2}$ but $x \\neq y$. In order to prove that bad pairs do not exist, we present two properties of them which provide an infinite descent. Property (i). If $(x, y)$ is a bad pair and $x<y$ then there exists a positive integer $z<x$ such that $(x, z)$ is also bad. Let $r=\\frac{\\left(4 x^{2}-1\\right)^{2}}{4 x y-1}$. Then $$ r=-r \\cdot(-1) \\equiv-r(4 x y-1)=-\\left(4 x^{2}-1\\right)^{2} \\equiv-1 \\quad(\\bmod 4 x) $$ and $r=4 x z-1$ with some positive integer $z$. From $x<y$ we obtain that $$ 4 x z-1=\\frac{\\left(4 x^{2}-1\\right)^{2}}{4 x y-1}<4 x^{2}-1 $$ and therefore $z<x$. By the construction, the number $4 x z-1$ is a divisor of $\\left(4 x^{2}-1\\right)^{2}$ so $(x, z)$ is a bad pair. Property (ii). If $(x, y)$ is a bad pair then $(y, x)$ is also bad. Since $1=1^{2} \\equiv(4 x y)^{2}(\\bmod 4 x y-1)$, we have $$ \\left(4 y^{2}-1\\right)^{2} \\equiv\\left(4 y^{2}-(4 x y)^{2}\\right)^{2}=16 y^{4}\\left(4 x^{2}-1\\right)^{2} \\equiv 0 \\quad(\\bmod 4 x y-1) $$ Hence, the number $4 x y-1$ divides $\\left(4 y^{2}-1\\right)^{2}$ as well. Now suppose that there exists at least one bad pair. Take a bad pair $(x, y)$ such that $2 x+y$ attains its smallest possible value. If $x<y$ then property (i) provides a bad pair $(x, z)$ with $z<y$ and thus $2 x+z<2 x+y$. Otherwise, if $y<x$, property (ii) yields that pair $(y, x)$ is also bad while $2 y+x<2 x+y$. Both cases contradict the assumption that $2 x+y$ is minimal; the Lemma is proved. To prove the problem statement, apply the Lemma for $x=k$ and $y=2 n$; the number $8 k n-1$ divides $\\left(4 k^{2}-1\\right)^{2}$ if and only if $k=2 n$. Hence, there is no such $n$ if $k$ is odd and $n=k / 2$ is the only solution if $k$ is even. Comment. The constant 4 in the Lemma can be replaced with an arbitrary integer greater than 1: if $a>1$ and $a x y-1$ divides $\\left(a x^{2}-1\\right)^{2}$ then $x=y$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N7", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "For a prime $p$ and a positive integer $n$, denote by $\\nu_{p}(n)$ the exponent of $p$ in the prime factorization of $n$ !. Given a positive integer $d$ and a finite set $\\left\\{p_{1}, \\ldots, p_{k}\\right\\}$ of primes. Show that there are infinitely many positive integers $n$ such that $d \\mid \\nu_{p_{i}}(n)$ for all $1 \\leq i \\leq k$. (India)", "solution": "For arbitrary prime $p$ and positive integer $n$, denote by $\\operatorname{ord}_{p}(n)$ the exponent of $p$ in $n$. Thus, $$ \\nu_{p}(n)=\\operatorname{ord}_{p}(n !)=\\sum_{i=1}^{n} \\operatorname{ord}_{p}(i) $$ Lemma. Let $p$ be a prime number, $q$ be a positive integer, $k$ and $r$ be positive integers such that $p^{k}>r$. Then $\\nu_{p}\\left(q p^{k}+r\\right)=\\nu_{p}\\left(q p^{k}\\right)+\\nu_{p}(r)$. Proof. We claim that $\\operatorname{ord}_{p}\\left(q p^{k}+i\\right)=\\operatorname{ord}_{p}(i)$ for all $0<i<p^{k}$. Actually, if $d=\\operatorname{ord}_{p}(i)$ then $d<k$, so $q p^{k}+i$ is divisible by $p^{d}$, but only the first term is divisible by $p^{d+1}$; hence the sum is not. Using this claim, we obtain $$ \\nu_{p}\\left(q p^{k}+r\\right)=\\sum_{i=1}^{q p^{k}} \\operatorname{ord}_{p}(i)+\\sum_{i=q p^{k}+1}^{q p^{k}+r} \\operatorname{ord}_{p}(i)=\\sum_{i=1}^{q p^{k}} \\operatorname{ord}_{p}(i)+\\sum_{i=1}^{r} \\operatorname{ord}_{p}(i)=\\nu_{p}\\left(q p^{k}\\right)+\\nu_{p}(r) . $$ For any integer $a$, denote by $\\bar{a}$ its residue modulo $d$. The addition of residues will also be performed modulo $d$, i. e. $\\bar{a}+\\bar{b}=\\overline{a+b}$. For any positive integer $n$, let $f(n)=\\left(f_{1}(n), \\ldots, f_{k}(n)\\right)$, where $f_{i}(n)=\\overline{\\nu_{p_{i}}(n)}$. Define the sequence $n_{1}=1, n_{\\ell+1}=\\left(p_{1} p_{2} \\ldots p_{k}\\right)^{n_{\\ell}}$. We claim that $$ f\\left(n_{\\ell_{1}}+n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}\\right)=f\\left(n_{\\ell_{1}}\\right)+f\\left(n_{\\ell_{2}}\\right)+\\ldots+f\\left(n_{\\ell_{m}}\\right) $$ for any $\\ell_{1}<\\ell_{2}<\\ldots<\\ell_{m}$. (The addition of $k$-tuples is componentwise.) The base case $m=1$ is trivial. Suppose that $m>1$. By the construction of the sequence, $p_{i}^{n_{\\ell_{1}}}$ divides $n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}$; clearly, $p_{i}^{n_{\\ell_{1}}}>n_{\\ell_{1}}$ for all $1 \\leq i \\leq k$. Therefore the Lemma can be applied for $p=p_{i}, k=r=n_{\\ell_{1}}$ and $q p^{k}=n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}$ to obtain $$ f_{i}\\left(n_{\\ell_{1}}+n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}\\right)=f_{i}\\left(n_{\\ell_{1}}\\right)+f_{i}\\left(n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}\\right) \\quad \\text { for all } 1 \\leq i \\leq k $$ and hence $$ f\\left(n_{\\ell_{1}}+n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}\\right)=f\\left(n_{\\ell_{1}}\\right)+f\\left(n_{\\ell_{2}}+\\ldots+n_{\\ell_{m}}\\right)=f\\left(n_{\\ell_{1}}\\right)+f\\left(n_{\\ell_{2}}\\right)+\\ldots+f\\left(n_{\\ell_{m}}\\right) $$ by the induction hypothesis. Now consider the values $f\\left(n_{1}\\right), f\\left(n_{2}\\right), \\ldots$ There exist finitely many possible values of $f$. Hence, there exists an infinite sequence of indices $\\ell_{1}<\\ell_{2}<\\ldots$ such that $f\\left(n_{\\ell_{1}}\\right)=f\\left(n_{\\ell_{2}}\\right)=\\ldots$ and thus $$ f\\left(n_{\\ell_{m+1}}+n_{\\ell_{m+2}}+\\ldots+n_{\\ell_{m+d}}\\right)=f\\left(n_{\\ell_{m+1}}\\right)+\\ldots+f\\left(n_{\\ell_{m+d}}\\right)=d \\cdot f\\left(n_{\\ell_{1}}\\right)=(\\overline{0}, \\ldots, \\overline{0}) $$ for all $m$. We have found infinitely many suitable numbers.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |
| {"year": "2007", "tier": "T0", "problem_label": "N7", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "For a prime $p$ and a positive integer $n$, denote by $\\nu_{p}(n)$ the exponent of $p$ in the prime factorization of $n$ !. Given a positive integer $d$ and a finite set $\\left\\{p_{1}, \\ldots, p_{k}\\right\\}$ of primes. Show that there are infinitely many positive integers $n$ such that $d \\mid \\nu_{p_{i}}(n)$ for all $1 \\leq i \\leq k$. (India)", "solution": "We use the same Lemma and definition of the function $f$. Let $S=\\{f(n): n \\in \\mathbb{N}\\}$. Obviously, set $S$ is finite. For every $s \\in S$ choose the minimal $n_{s}$ such that $f\\left(n_{s}\\right)=s$. Denote $N=\\max _{s \\in S} n_{s}$. Moreover, let $g$ be an integer such that $p_{i}^{g}>N$ for each $i=1,2, \\ldots, k$. Let $P=\\left(p_{1} p_{2} \\ldots p_{k}\\right)^{g}$. We claim that $$ \\{f(n) \\mid n \\in[m P, m P+N]\\}=S $$ for every positive integer $m$. In particular, since $(\\overline{0}, \\ldots, \\overline{0})=f(1) \\in S$, it follows that for an arbitrary $m$ there exists $n \\in[m P, m P+N]$ such that $f(n)=(\\overline{0}, \\ldots, \\overline{0})$. So there are infinitely many suitable numbers. To prove (1), let $a_{i}=f_{i}(m P)$. Consider all numbers of the form $n_{m, s}=m P+n_{s}$ with $s=\\left(s_{1}, \\ldots, s_{k}\\right) \\in S$ (clearly, all $n_{m, s}$ belong to $[m P, m P+N]$ ). Since $n_{s} \\leq N<p_{i}^{g}$ and $p_{i}^{g} \\mid m P$, we can apply the Lemma for the values $p=p_{i}, r=n_{s}, k=g, q p^{k}=m P$ to obtain $$ f_{i}\\left(n_{m, s}\\right)=f_{i}(m P)+f_{i}\\left(n_{s}\\right)=a_{i}+s_{i} \\text {; } $$ hence for distinct $s, t \\in S$ we have $f\\left(n_{m, s}\\right) \\neq f\\left(n_{m, t}\\right)$. Thus, the function $f$ attains at least $|S|$ distinct values in $[m P, m P+N]$. Since all these values belong to $S, f$ should attain all possible values in $[m P, m P+N]$. Comment. Both solutions can be extended to prove the following statements. Claim 1. For any $K$ there exist infinitely many $n$ divisible by $K$, such that $d \\mid \\nu_{p_{i}}(n)$ for each $i$. Claim 2. For any $s \\in S$, there exist infinitely many $n \\in \\mathbb{N}$ such that $f(n)=s$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2007SL.jsonl"}} | |