| {"year": "2018", "tier": "T0", "problem_label": "A1", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $\\mathbb{Q}_{>0}$ denote the set of all positive rational numbers. Determine all functions $f: \\mathbb{Q}_{>0} \\rightarrow \\mathbb{Q}_{>0}$ satisfying for all $x, y \\in \\mathbb{Q}_{>0}$. $$ f\\left(x^{2} f(y)^{2}\\right)=f(x)^{2} f(y) $$ (Switzerland)", "solution": "Take any $a, b \\in \\mathbb{Q}_{>0}$. By substituting $x=f(a), y=b$ and $x=f(b), y=a$ into $(*)$ we get $$ f(f(a))^{2} f(b)=f\\left(f(a)^{2} f(b)^{2}\\right)=f(f(b))^{2} f(a) $$ which yields $$ \\frac{f(f(a))^{2}}{f(a)}=\\frac{f(f(b))^{2}}{f(b)} \\quad \\text { for all } a, b \\in \\mathbb{Q}_{>0} $$ In other words, this shows that there exists a constant $C \\in \\mathbb{Q}_{>0}$ such that $f(f(a))^{2}=C f(a)$, or $$ \\left(\\frac{f(f(a))}{C}\\right)^{2}=\\frac{f(a)}{C} \\quad \\text { for all } a \\in \\mathbb{Q}_{>0} \\text {. } $$ Denote by $f^{n}(x)=\\underbrace{f(f(\\ldots(f}_{n}(x)) \\ldots))$ the $n^{\\text {th }}$ iteration of $f$. Equality (1) yields $$ \\frac{f(a)}{C}=\\left(\\frac{f^{2}(a)}{C}\\right)^{2}=\\left(\\frac{f^{3}(a)}{C}\\right)^{4}=\\cdots=\\left(\\frac{f^{n+1}(a)}{C}\\right)^{2^{n}} $$ for all positive integer $n$. So, $f(a) / C$ is the $2^{n}$-th power of a rational number for all positive integer $n$. This is impossible unless $f(a) / C=1$, since otherwise the exponent of some prime in the prime decomposition of $f(a) / C$ is not divisible by sufficiently large powers of 2 . Therefore, $f(a)=C$ for all $a \\in \\mathbb{Q}_{>0}$. Finally, after substituting $f \\equiv C$ into (*) we get $C=C^{3}$, whence $C=1$. So $f(x) \\equiv 1$ is the unique function satisfying $(*)$. Comment 1. There are several variations of the solution above. For instance, one may start with finding $f(1)=1$. To do this, let $d=f(1)$. By substituting $x=y=1$ and $x=d^{2}, y=1$ into (*) we get $f\\left(d^{2}\\right)=d^{3}$ and $f\\left(d^{6}\\right)=f\\left(d^{2}\\right)^{2} \\cdot d=d^{7}$. By substituting now $x=1, y=d^{2}$ we obtain $f\\left(d^{6}\\right)=d^{2} \\cdot d^{3}=d^{5}$. Therefore, $d^{7}=f\\left(d^{6}\\right)=d^{5}$, whence $d=1$. After that, the rest of the solution simplifies a bit, since we already know that $C=\\frac{f(f(1))^{2}}{f(1)}=1$. Hence equation (1) becomes merely $f(f(a))^{2}=f(a)$, which yields $f(a)=1$ in a similar manner. Comment 2. There exist nonconstant functions $f: \\mathbb{R}^{+} \\rightarrow \\mathbb{R}^{+}$satisfying $(*)$ for all real $x, y>0-$ e.g., $f(x)=\\sqrt{x}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A2", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find all positive integers $n \\geqslant 3$ for which there exist real numbers $a_{1}, a_{2}, \\ldots, a_{n}$, $a_{n+1}=a_{1}, a_{n+2}=a_{2}$ such that $$ a_{i} a_{i+1}+1=a_{i+2} $$ for all $i=1,2, \\ldots, n$. (Slovakia)", "solution": "For the sake of convenience, extend the sequence $a_{1}, \\ldots, a_{n+2}$ to an infinite periodic sequence with period $n$. ( $n$ is not necessarily the shortest period.) If $n$ is divisible by 3 , then $\\left(a_{1}, a_{2}, \\ldots\\right)=(-1,-1,2,-1,-1,2, \\ldots)$ is an obvious solution. We will show that in every periodic sequence satisfying the recurrence, each positive term is followed by two negative values, and after them the next number is positive again. From this, it follows that $n$ is divisible by 3 . If the sequence contains two consecutive positive numbers $a_{i}, a_{i+1}$, then $a_{i+2}=a_{i} a_{i+1}+1>1$, so the next value is positive as well; by induction, all numbers are positive and greater than 1 . But then $a_{i+2}=a_{i} a_{i+1}+1 \\geqslant 1 \\cdot a_{i+1}+1>a_{i+1}$ for every index $i$, which is impossible: our sequence is periodic, so it cannot increase everywhere. If the number 0 occurs in the sequence, $a_{i}=0$ for some index $i$, then it follows that $a_{i+1}=a_{i-1} a_{i}+1$ and $a_{i+2}=a_{i} a_{i+1}+1$ are two consecutive positive elements in the sequences and we get the same contradiction again. Notice that after any two consecutive negative numbers the next one must be positive: if $a_{i}<0$ and $a_{i+1}<0$, then $a_{i+2}=a_{1} a_{i+1}+1>1>0$. Hence, the positive and negative numbers follow each other in such a way that each positive term is followed by one or two negative values and then comes the next positive term. Consider the case when the positive and negative values alternate. So, if $a_{i}$ is a negative value then $a_{i+1}$ is positive, $a_{i+2}$ is negative and $a_{i+3}$ is positive again. Notice that $a_{i} a_{i+1}+1=a_{i+2}<0<a_{i+3}=a_{i+1} a_{i+2}+1$; by $a_{i+1}>0$ we conclude $a_{i}<a_{i+2}$. Hence, the negative values form an infinite increasing subsequence, $a_{i}<a_{i+2}<a_{i+4}<\\ldots$, which is not possible, because the sequence is periodic. The only case left is when there are consecutive negative numbers in the sequence. Suppose that $a_{i}$ and $a_{i+1}$ are negative; then $a_{i+2}=a_{i} a_{i+1}+1>1$. The number $a_{i+3}$ must be negative. We show that $a_{i+4}$ also must be negative. Notice that $a_{i+3}$ is negative and $a_{i+4}=a_{i+2} a_{i+3}+1<1<a_{i} a_{i+1}+1=a_{i+2}$, so $$ a_{i+5}-a_{i+4}=\\left(a_{i+3} a_{i+4}+1\\right)-\\left(a_{i+2} a_{i+3}+1\\right)=a_{i+3}\\left(a_{i+4}-a_{i+2}\\right)>0, $$ therefore $a_{i+5}>a_{i+4}$. Since at most one of $a_{i+4}$ and $a_{i+5}$ can be positive, that means that $a_{i+4}$ must be negative. Now $a_{i+3}$ and $a_{i+4}$ are negative and $a_{i+5}$ is positive; so after two negative and a positive terms, the next three terms repeat the same pattern. That completes the solution.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A2", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find all positive integers $n \\geqslant 3$ for which there exist real numbers $a_{1}, a_{2}, \\ldots, a_{n}$, $a_{n+1}=a_{1}, a_{n+2}=a_{2}$ such that $$ a_{i} a_{i+1}+1=a_{i+2} $$ for all $i=1,2, \\ldots, n$. (Slovakia)", "solution": "We prove that the shortest period of the sequence must be 3 . Then it follows that $n$ must be divisible by 3 . Notice that the equation $x^{2}+1=x$ has no real root, so the numbers $a_{1}, \\ldots, a_{n}$ cannot be all equal, hence the shortest period of the sequence cannot be 1 . By applying the recurrence relation for $i$ and $i+1$, $$ \\begin{gathered} \\left(a_{i+2}-1\\right) a_{i+2}=a_{i} a_{i+1} a_{i+2}=a_{i}\\left(a_{i+3}-1\\right), \\quad \\text { so } \\\\ a_{i+2}^{2}-a_{i} a_{i+3}=a_{i+2}-a_{i} . \\end{gathered} $$ By summing over $i=1,2, \\ldots, n$, we get $$ \\sum_{i=1}^{n}\\left(a_{i}-a_{i+3}\\right)^{2}=0 $$ That proves that $a_{i}=a_{i+3}$ for every index $i$, so the sequence $a_{1}, a_{2}, \\ldots$ is indeed periodic with period 3. The shortest period cannot be 1 , so it must be 3 ; therefore, $n$ is divisible by 3 . Comment. By solving the system of equations $a b+1=c, \\quad b c+1=a, \\quad c a+1=b$, it can be seen that the pattern $(-1,-1,2)$ is repeated in all sequences satisfying the problem conditions.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A3", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Given any set $S$ of positive integers, show that at least one of the following two assertions holds: (1) There exist distinct finite subsets $F$ and $G$ of $S$ such that $\\sum_{x \\in F} 1 / x=\\sum_{x \\in G} 1 / x$; (2) There exists a positive rational number $r<1$ such that $\\sum_{x \\in F} 1 / x \\neq r$ for all finite subsets $F$ of $S$. (Luxembourg)", "solution": "Argue indirectly. Agree, as usual, that the empty sum is 0 to consider rationals in $[0,1)$; adjoining 0 causes no harm, since $\\sum_{x \\in F} 1 / x=0$ for no nonempty finite subset $F$ of $S$. For every rational $r$ in $[0,1)$, let $F_{r}$ be the unique finite subset of $S$ such that $\\sum_{x \\in F_{r}} 1 / x=r$. The argument hinges on the lemma below. Lemma. If $x$ is a member of $S$ and $q$ and $r$ are rationals in $[0,1)$ such that $q-r=1 / x$, then $x$ is a member of $F_{q}$ if and only if it is not one of $F_{r}$. Proof. If $x$ is a member of $F_{q}$, then $$ \\sum_{y \\in F_{q} \\backslash\\{x\\}} \\frac{1}{y}=\\sum_{y \\in F_{q}} \\frac{1}{y}-\\frac{1}{x}=q-\\frac{1}{x}=r=\\sum_{y \\in F_{r}} \\frac{1}{y} $$ so $F_{r}=F_{q} \\backslash\\{x\\}$, and $x$ is not a member of $F_{r}$. Conversely, if $x$ is not a member of $F_{r}$, then $$ \\sum_{y \\in F_{r} \\cup\\{x\\}} \\frac{1}{y}=\\sum_{y \\in F_{r}} \\frac{1}{y}+\\frac{1}{x}=r+\\frac{1}{x}=q=\\sum_{y \\in F_{q}} \\frac{1}{y} $$ so $F_{q}=F_{r} \\cup\\{x\\}$, and $x$ is a member of $F_{q}$. Consider now an element $x$ of $S$ and a positive rational $r<1$. Let $n=\\lfloor r x\\rfloor$ and consider the sets $F_{r-k / x}, k=0, \\ldots, n$. Since $0 \\leqslant r-n / x<1 / x$, the set $F_{r-n / x}$ does not contain $x$, and a repeated application of the lemma shows that the $F_{r-(n-2 k) / x}$ do not contain $x$, whereas the $F_{r-(n-2 k-1) / x}$ do. Consequently, $x$ is a member of $F_{r}$ if and only if $n$ is odd. Finally, consider $F_{2 / 3}$. By the preceding, $\\lfloor 2 x / 3\\rfloor$ is odd for each $x$ in $F_{2 / 3}$, so $2 x / 3$ is not integral. Since $F_{2 / 3}$ is finite, there exists a positive rational $\\varepsilon$ such that $\\lfloor(2 / 3-\\varepsilon) x\\rfloor=\\lfloor 2 x / 3\\rfloor$ for all $x$ in $F_{2 / 3}$. This implies that $F_{2 / 3}$ is a subset of $F_{2 / 3-\\varepsilon}$ which is impossible. Comment. The solution above can be adapted to show that the problem statement still holds, if the condition $r<1$ in (2) is replaced with $r<\\delta$, for an arbitrary positive $\\delta$. This yields that, if $S$ does not satisfy (1), then there exist infinitely many positive rational numbers $r<1$ such that $\\sum_{x \\in F} 1 / x \\neq r$ for all finite subsets $F$ of $S$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A3", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Given any set $S$ of positive integers, show that at least one of the following two assertions holds: (1) There exist distinct finite subsets $F$ and $G$ of $S$ such that $\\sum_{x \\in F} 1 / x=\\sum_{x \\in G} 1 / x$; (2) There exists a positive rational number $r<1$ such that $\\sum_{x \\in F} 1 / x \\neq r$ for all finite subsets $F$ of $S$. (Luxembourg)", "solution": "A finite $S$ clearly satisfies (2), so let $S$ be infinite. If $S$ fails both conditions, so does $S \\backslash\\{1\\}$. We may and will therefore assume that $S$ consists of integers greater than 1 . Label the elements of $S$ increasingly $x_{1}<x_{2}<\\cdots$, where $x_{1} \\geqslant 2$. We first show that $S$ satisfies (2) if $x_{n+1} \\geqslant 2 x_{n}$ for all $n$. In this case, $x_{n} \\geqslant 2^{n-1} x_{1}$ for all $n$, so $$ s=\\sum_{n \\geqslant 1} \\frac{1}{x_{n}} \\leqslant \\sum_{n \\geqslant 1} \\frac{1}{2^{n-1} x_{1}}=\\frac{2}{x_{1}} $$ If $x_{1} \\geqslant 3$, or $x_{1}=2$ and $x_{n+1}>2 x_{n}$ for some $n$, then $\\sum_{x \\in F} 1 / x<s<1$ for every finite subset $F$ of $S$, so $S$ satisfies (2); and if $x_{1}=2$ and $x_{n+1}=2 x_{n}$ for all $n$, that is, $x_{n}=2^{n}$ for all $n$, then every finite subset $F$ of $S$ consists of powers of 2 , so $\\sum_{x \\in F} 1 / x \\neq 1 / 3$ and again $S$ satisfies (2). Finally, we deal with the case where $x_{n+1}<2 x_{n}$ for some $n$. Consider the positive rational $r=1 / x_{n}-1 / x_{n+1}<1 / x_{n+1}$. If $r=\\sum_{x \\in F} 1 / x$ for no finite subset $F$ of $S$, then $S$ satisfies (2). We now assume that $r=\\sum_{x \\in F_{0}} 1 / x$ for some finite subset $F_{0}$ of $S$, and show that $S$ satisfies (1). Since $\\sum_{x \\in F_{0}} 1 / x=r<1 / x_{n+1}$, it follows that $x_{n+1}$ is not a member of $F_{0}$, so $$ \\sum_{x \\in F_{0} \\cup\\left\\{x_{n+1}\\right\\}} \\frac{1}{x}=\\sum_{x \\in F_{0}} \\frac{1}{x}+\\frac{1}{x_{n+1}}=r+\\frac{1}{x_{n+1}}=\\frac{1}{x_{n}} $$ Consequently, $F=F_{0} \\cup\\left\\{x_{n+1}\\right\\}$ and $G=\\left\\{x_{n}\\right\\}$ are distinct finite subsets of $S$ such that $\\sum_{x \\in F} 1 / x=\\sum_{x \\in G} 1 / x$, and $S$ satisfies (1).", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A4", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $a_{0}, a_{1}, a_{2}, \\ldots$ be a sequence of real numbers such that $a_{0}=0, a_{1}=1$, and for every $n \\geqslant 2$ there exists $1 \\leqslant k \\leqslant n$ satisfying $$ a_{n}=\\frac{a_{n-1}+\\cdots+a_{n-k}}{k} $$ Find the maximal possible value of $a_{2018}-a_{2017}$. (Belgium)", "solution": "The claimed maximal value is achieved at $$ \\begin{gathered} a_{1}=a_{2}=\\cdots=a_{2016}=1, \\quad a_{2017}=\\frac{a_{2016}+\\cdots+a_{0}}{2017}=1-\\frac{1}{2017}, \\\\ a_{2018}=\\frac{a_{2017}+\\cdots+a_{1}}{2017}=1-\\frac{1}{2017^{2}} . \\end{gathered} $$ Now we need to show that this value is optimal. For brevity, we use the notation $$ S(n, k)=a_{n-1}+a_{n-2}+\\cdots+a_{n-k} \\quad \\text { for nonnegative integers } k \\leqslant n \\text {. } $$ In particular, $S(n, 0)=0$ and $S(n, 1)=a_{n-1}$. In these terms, for every integer $n \\geqslant 2$ there exists a positive integer $k \\leqslant n$ such that $a_{n}=S(n, k) / k$. For every integer $n \\geqslant 1$ we define $$ M_{n}=\\max _{1 \\leqslant k \\leqslant n} \\frac{S(n, k)}{k}, \\quad m_{n}=\\min _{1 \\leqslant k \\leqslant n} \\frac{S(n, k)}{k}, \\quad \\text { and } \\quad \\Delta_{n}=M_{n}-m_{n} \\geqslant 0 . $$ By definition, $a_{n} \\in\\left[m_{n}, M_{n}\\right]$ for all $n \\geqslant 2$; on the other hand, $a_{n-1}=S(n, 1) / 1 \\in\\left[m_{n}, M_{n}\\right]$. Therefore, $$ a_{2018}-a_{2017} \\leqslant M_{2018}-m_{2018}=\\Delta_{2018}, $$ and we are interested in an upper bound for $\\Delta_{2018}$. Also by definition, for any $0<k \\leqslant n$ we have $k m_{n} \\leqslant S(n, k) \\leqslant k M_{n}$; notice that these inequalities are also valid for $k=0$. Claim 1. For every $n>2$, we have $\\Delta_{n} \\leqslant \\frac{n-1}{n} \\Delta_{n-1}$. Proof. Choose positive integers $k, \\ell \\leqslant n$ such that $M_{n}=S(n, k) / k$ and $m_{n}=S(n, \\ell) / \\ell$. We have $S(n, k)=a_{n-1}+S(n-1, k-1)$, so $$ k\\left(M_{n}-a_{n-1}\\right)=S(n, k)-k a_{n-1}=S(n-1, k-1)-(k-1) a_{n-1} \\leqslant(k-1)\\left(M_{n-1}-a_{n-1}\\right), $$ since $S(n-1, k-1) \\leqslant(k-1) M_{n-1}$. Similarly, we get $$ \\ell\\left(a_{n-1}-m_{n}\\right)=(\\ell-1) a_{n-1}-S(n-1, \\ell-1) \\leqslant(\\ell-1)\\left(a_{n-1}-m_{n-1}\\right) . $$ Since $m_{n-1} \\leqslant a_{n-1} \\leqslant M_{n-1}$ and $k, \\ell \\leqslant n$, the obtained inequalities yield $$ \\begin{array}{ll} M_{n}-a_{n-1} \\leqslant \\frac{k-1}{k}\\left(M_{n-1}-a_{n-1}\\right) \\leqslant \\frac{n-1}{n}\\left(M_{n-1}-a_{n-1}\\right) \\quad \\text { and } \\\\ a_{n-1}-m_{n} \\leqslant \\frac{\\ell-1}{\\ell}\\left(a_{n-1}-m_{n-1}\\right) \\leqslant \\frac{n-1}{n}\\left(a_{n-1}-m_{n-1}\\right) . \\end{array} $$ Therefore, $$ \\Delta_{n}=\\left(M_{n}-a_{n-1}\\right)+\\left(a_{n-1}-m_{n}\\right) \\leqslant \\frac{n-1}{n}\\left(\\left(M_{n-1}-a_{n-1}\\right)+\\left(a_{n-1}-m_{n-1}\\right)\\right)=\\frac{n-1}{n} \\Delta_{n-1} . $$ Back to the problem, if $a_{n}=1$ for all $n \\leqslant 2017$, then $a_{2018} \\leqslant 1$ and hence $a_{2018}-a_{2017} \\leqslant 0$. Otherwise, let $2 \\leqslant q \\leqslant 2017$ be the minimal index with $a_{q}<1$. We have $S(q, i)=i$ for all $i=1,2, \\ldots, q-1$, while $S(q, q)=q-1$. Therefore, $a_{q}<1$ yields $a_{q}=S(q, q) / q=1-\\frac{1}{q}$. Now we have $S(q+1, i)=i-\\frac{1}{q}$ for $i=1,2, \\ldots, q$, and $S(q+1, q+1)=q-\\frac{1}{q}$. This gives us $$ m_{q+1}=\\frac{S(q+1,1)}{1}=\\frac{S(q+1, q+1)}{q+1}=\\frac{q-1}{q} \\quad \\text { and } \\quad M_{q+1}=\\frac{S(q+1, q)}{q}=\\frac{q^{2}-1}{q^{2}} $$ so $\\Delta_{q+1}=M_{q+1}-m_{q+1}=(q-1) / q^{2}$. Denoting $N=2017 \\geqslant q$ and using Claim 1 for $n=q+2, q+3, \\ldots, N+1$ we finally obtain $$ \\Delta_{N+1} \\leqslant \\frac{q-1}{q^{2}} \\cdot \\frac{q+1}{q+2} \\cdot \\frac{q+2}{q+3} \\cdots \\frac{N}{N+1}=\\frac{1}{N+1}\\left(1-\\frac{1}{q^{2}}\\right) \\leqslant \\frac{1}{N+1}\\left(1-\\frac{1}{N^{2}}\\right)=\\frac{N-1}{N^{2}} $$ as required. Comment 1. One may check that the maximal value of $a_{2018}-a_{2017}$ is attained at the unique sequence, which is presented in the solution above. Comment 2. An easier question would be to determine the maximal value of $\\left|a_{2018}-a_{2017}\\right|$. In this version, the answer $\\frac{1}{2018}$ is achieved at $$ a_{1}=a_{2}=\\cdots=a_{2017}=1, \\quad a_{2018}=\\frac{a_{2017}+\\cdots+a_{0}}{2018}=1-\\frac{1}{2018} . $$ To prove that this value is optimal, it suffices to notice that $\\Delta_{2}=\\frac{1}{2}$ and to apply Claim 1 obtaining $$ \\left|a_{2018}-a_{2017}\\right| \\leqslant \\Delta_{2018} \\leqslant \\frac{1}{2} \\cdot \\frac{2}{3} \\cdots \\frac{2017}{2018}=\\frac{1}{2018} . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A4", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $a_{0}, a_{1}, a_{2}, \\ldots$ be a sequence of real numbers such that $a_{0}=0, a_{1}=1$, and for every $n \\geqslant 2$ there exists $1 \\leqslant k \\leqslant n$ satisfying $$ a_{n}=\\frac{a_{n-1}+\\cdots+a_{n-k}}{k} $$ Find the maximal possible value of $a_{2018}-a_{2017}$. (Belgium)", "solution": "We present a different proof of the estimate $a_{2018}-a_{2017} \\leqslant \\frac{2016}{2017^{2}}$. We keep the same notations of $S(n, k), m_{n}$ and $M_{n}$ from the previous solution. Notice that $S(n, n)=S(n, n-1)$, as $a_{0}=0$. Also notice that for $0 \\leqslant k \\leqslant \\ell \\leqslant n$ we have $S(n, \\ell)=S(n, k)+S(n-k, \\ell-k)$. Claim 2. For every positive integer $n$, we have $m_{n} \\leqslant m_{n+1}$ and $M_{n+1} \\leqslant M_{n}$, so the segment $\\left[m_{n+1}, M_{n+1}\\right]$ is contained in $\\left[m_{n}, M_{n}\\right]$. Proof. Choose a positive integer $k \\leqslant n+1$ such that $m_{n+1}=S(n+1, k) / k$. Then we have $$ k m_{n+1}=S(n+1, k)=a_{n}+S(n, k-1) \\geqslant m_{n}+(k-1) m_{n}=k m_{n}, $$ which establishes the first inequality in the Claim. The proof of the second inequality is similar. Claim 3. For every positive integers $k \\geqslant n$, we have $m_{n} \\leqslant a_{k} \\leqslant M_{n}$. Proof. By Claim 2, we have $\\left[m_{k}, M_{k}\\right] \\subseteq\\left[m_{k-1}, M_{k-1}\\right] \\subseteq \\cdots \\subseteq\\left[m_{n}, M_{n}\\right]$. Since $a_{k} \\in\\left[m_{k}, M_{k}\\right]$, the claim follows. Claim 4. For every integer $n \\geqslant 2$, we have $M_{n}=S(n, n-1) /(n-1)$ and $m_{n}=S(n, n) / n$. Proof. We use induction on $n$. The base case $n=2$ is routine. To perform the induction step, we need to prove the inequalities $$ \\frac{S(n, n)}{n} \\leqslant \\frac{S(n, k)}{k} \\quad \\text { and } \\quad \\frac{S(n, k)}{k} \\leqslant \\frac{S(n, n-1)}{n-1} $$ for every positive integer $k \\leqslant n$. Clearly, these inequalities hold for $k=n$ and $k=n-1$, as $S(n, n)=S(n, n-1)>0$. In the sequel, we assume that $k<n-1$. Now the first inequality in (1) rewrites as $n S(n, k) \\geqslant k S(n, n)=k(S(n, k)+S(n-k, n-k))$, or, cancelling the terms occurring on both parts, as $$ (n-k) S(n, k) \\geqslant k S(n-k, n-k) \\Longleftrightarrow S(n, k) \\geqslant k \\cdot \\frac{S(n-k, n-k)}{n-k} $$ By the induction hypothesis, we have $S(n-k, n-k) /(n-k)=m_{n-k}$. By Claim 3, we get $a_{n-i} \\geqslant m_{n-k}$ for all $i=1,2, \\ldots, k$. Summing these $k$ inequalities we obtain $$ S(n, k) \\geqslant k m_{n-k}=k \\cdot \\frac{S(n-k, n-k)}{n-k} $$ as required. The second inequality in (1) is proved similarly. Indeed, this inequality is equivalent to $$ \\begin{aligned} (n-1) S(n, k) \\leqslant k S(n, n-1) & \\Longleftrightarrow(n-k-1) S(n, k) \\leqslant k S(n-k, n-k-1) \\\\ & \\Longleftrightarrow S(n, k) \\leqslant k \\cdot \\frac{S(n-k, n-k-1)}{n-k-1}=k M_{n-k} ; \\end{aligned} $$ the last inequality follows again from Claim 3, as each term in $S(n, k)$ is at most $M_{n-k}$. Now we can prove the required estimate for $a_{2018}-a_{2017}$. Set $N=2017$. By Claim 4 , $$ \\begin{aligned} a_{N+1}-a_{N} \\leqslant M_{N+1}-a_{N}=\\frac{S(N+1, N)}{N}-a_{N} & =\\frac{a_{N}+S(N, N-1)}{N}-a_{N} \\\\ & =\\frac{S(N, N-1)}{N}-\\frac{N-1}{N} \\cdot a_{N} . \\end{aligned} $$ On the other hand, the same Claim yields $$ a_{N} \\geqslant m_{N}=\\frac{S(N, N)}{N}=\\frac{S(N, N-1)}{N} . $$ Noticing that each term in $S(N, N-1)$ is at most 1 , so $S(N, N-1) \\leqslant N-1$, we finally obtain $$ a_{N+1}-a_{N} \\leqslant \\frac{S(N, N-1)}{N}-\\frac{N-1}{N} \\cdot \\frac{S(N, N-1)}{N}=\\frac{S(N, N-1)}{N^{2}} \\leqslant \\frac{N-1}{N^{2}} . $$ Comment 1. Claim 1 in Solution 1 can be deduced from Claims 2 and 4 in Solution 2. By Claim 4 we have $M_{n}=\\frac{S(n, n-1)}{n-1}$ and $m_{n}=\\frac{S(n, n)}{n}=\\frac{S(n, n-1)}{n}$. It follows that $\\Delta_{n}=M_{n}-m_{n}=$ $\\frac{S(n, n-1)}{(n-1) n}$ and so $M_{n}=n \\Delta_{n}$ and $m_{n}=(n-1) \\Delta_{n}$ Similarly, $M_{n-1}=(n-1) \\Delta_{n-1}$ and $m_{n-1}=(n-2) \\Delta_{n-1}$. Then the inequalities $m_{n-1} \\leqslant m_{n}$ and $M_{n} \\leqslant M_{n-1}$ from Claim 2 write as $(n-2) \\Delta_{n-1} \\leqslant(n-1) \\Delta_{n}$ and $n \\Delta_{n} \\leqslant(n-1) \\Delta_{n-1}$. Hence we have the double inequality $$ \\frac{n-2}{n-1} \\Delta_{n-1} \\leqslant \\Delta_{n} \\leqslant \\frac{n-1}{n} \\Delta_{n-1} $$ Comment 2. Both solutions above discuss the properties of an arbitrary sequence satisfying the problem conditions. Instead, one may investigate only an optimal sequence which maximises the value of $a_{2018}-a_{2017}$. Here we present an observation which allows to simplify such investigation - for instance, the proofs of Claim 1 in Solution 1 and Claim 4 in Solution 2. The sequence $\\left(a_{n}\\right)$ is uniquely determined by choosing, for every $n \\geqslant 2$, a positive integer $k(n) \\leqslant n$ such that $a_{n}=S(n, k(n)) / k(n)$. Take an arbitrary $2 \\leqslant n_{0} \\leqslant 2018$, and assume that all such integers $k(n)$, for $n \\neq n_{0}$, are fixed. Then, for every $n$, the value of $a_{n}$ is a linear function in $a_{n_{0}}$ (whose possible values constitute some discrete subset of $\\left[m_{n_{0}}, M_{n_{0}}\\right]$ containing both endpoints). Hence, $a_{2018}-a_{2017}$ is also a linear function in $a_{n_{0}}$, so it attains its maximal value at one of the endpoints of the segment $\\left[m_{n_{0}}, M_{n_{0}}\\right]$. This shows that, while dealing with an optimal sequence, we may assume $a_{n} \\in\\left\\{m_{n}, M_{n}\\right\\}$ for all $2 \\leqslant n \\leqslant 2018$. Now one can easily see that, if $a_{n}=m_{n}$, then $m_{n+1}=m_{n}$ and $M_{n+1} \\leqslant \\frac{m_{n}+n M_{n}}{n+1} ;$ similar estimates hold in the case $a_{n}=M_{n}$. This already establishes Claim 1, and simplifies the inductive proof of Claim 4, both applied to an optimal sequence.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A5", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Determine all functions $f:(0, \\infty) \\rightarrow \\mathbb{R}$ satisfying $$ \\left(x+\\frac{1}{x}\\right) f(y)=f(x y)+f\\left(\\frac{y}{x}\\right) $$ for all $x, y>0$. (South Korea)", "solution": "Fix a real number $a>1$, and take a new variable $t$. For the values $f(t), f\\left(t^{2}\\right)$, $f(a t)$ and $f\\left(a^{2} t^{2}\\right)$, the relation (1) provides a system of linear equations: $$ \\begin{array}{llll} x=y=t: & \\left(t+\\frac{1}{t}\\right) f(t) & =f\\left(t^{2}\\right)+f(1) \\\\ x=\\frac{t}{a}, y=a t: & \\left(\\frac{t}{a}+\\frac{a}{t}\\right) f(a t) & =f\\left(t^{2}\\right)+f\\left(a^{2}\\right) \\\\ x=a^{2} t, y=t: & \\left(a^{2} t+\\frac{1}{a^{2} t}\\right) f(t) & =f\\left(a^{2} t^{2}\\right)+f\\left(\\frac{1}{a^{2}}\\right) \\\\ x=y=a t: & \\left(a t+\\frac{1}{a t}\\right) f(a t) & =f\\left(a^{2} t^{2}\\right)+f(1) \\end{array} $$ In order to eliminate $f\\left(t^{2}\\right)$, take the difference of (2a) and (2b); from (2c) and (2d) eliminate $f\\left(a^{2} t^{2}\\right)$; then by taking a linear combination, eliminate $f(a t)$ as well: $$ \\begin{gathered} \\left(t+\\frac{1}{t}\\right) f(t)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right) f(a t)=f(1)-f\\left(a^{2}\\right) \\text { and } \\\\ \\left(a^{2} t+\\frac{1}{a^{2} t}\\right) f(t)-\\left(a t+\\frac{1}{a t}\\right) f(a t)=f\\left(1 / a^{2}\\right)-f(1), \\text { so } \\\\ \\left(\\left(a t+\\frac{1}{a t}\\right)\\left(t+\\frac{1}{t}\\right)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right)\\left(a^{2} t+\\frac{1}{a^{2} t}\\right)\\right) f(t) \\\\ =\\left(a t+\\frac{1}{a t}\\right)\\left(f(1)-f\\left(a^{2}\\right)\\right)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right)\\left(f\\left(1 / a^{2}\\right)-f(1)\\right) . \\end{gathered} $$ Notice that on the left-hand side, the coefficient of $f(t)$ is nonzero and does not depend on $t$ : $$ \\left(a t+\\frac{1}{a t}\\right)\\left(t+\\frac{1}{t}\\right)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right)\\left(a^{2} t+\\frac{1}{a^{2} t}\\right)=a+\\frac{1}{a}-\\left(a^{3}+\\frac{1}{a^{3}}\\right)<0 . $$ After dividing by this fixed number, we get $$ f(t)=C_{1} t+\\frac{C_{2}}{t} $$ where the numbers $C_{1}$ and $C_{2}$ are expressed in terms of $a, f(1), f\\left(a^{2}\\right)$ and $f\\left(1 / a^{2}\\right)$, and they do not depend on $t$. The functions of the form (3) satisfy the equation: $$ \\left(x+\\frac{1}{x}\\right) f(y)=\\left(x+\\frac{1}{x}\\right)\\left(C_{1} y+\\frac{C_{2}}{y}\\right)=\\left(C_{1} x y+\\frac{C_{2}}{x y}\\right)+\\left(C_{1} \\frac{y}{x}+C_{2} \\frac{x}{y}\\right)=f(x y)+f\\left(\\frac{y}{x}\\right) . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A5", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Determine all functions $f:(0, \\infty) \\rightarrow \\mathbb{R}$ satisfying $$ \\left(x+\\frac{1}{x}\\right) f(y)=f(x y)+f\\left(\\frac{y}{x}\\right) $$ for all $x, y>0$. (South Korea)", "solution": "We start with an observation. If we substitute $x=a \\neq 1$ and $y=a^{n}$ in (1), we obtain $$ f\\left(a^{n+1}\\right)-\\left(a+\\frac{1}{a}\\right) f\\left(a^{n}\\right)+f\\left(a^{n-1}\\right)=0 . $$ For the sequence $z_{n}=a^{n}$, this is a homogeneous linear recurrence of the second order, and its characteristic polynomial is $t^{2}-\\left(a+\\frac{1}{a}\\right) t+1=(t-a)\\left(t-\\frac{1}{a}\\right)$ with two distinct nonzero roots, namely $a$ and $1 / a$. As is well-known, the general solution is $z_{n}=C_{1} a^{n}+C_{2}(1 / a)^{n}$ where the index $n$ can be as well positive as negative. Of course, the numbers $C_{1}$ and $C_{2}$ may depend of the choice of $a$, so in fact we have two functions, $C_{1}$ and $C_{2}$, such that $$ f\\left(a^{n}\\right)=C_{1}(a) \\cdot a^{n}+\\frac{C_{2}(a)}{a^{n}} \\quad \\text { for every } a \\neq 1 \\text { and every integer } n \\text {. } $$ The relation (4) can be easily extended to rational values of $n$, so we may conjecture that $C_{1}$ and $C_{2}$ are constants, and whence $f(t)=C_{1} t+\\frac{C_{2}}{t}$. As it was seen in the previous solution, such functions indeed satisfy (1). The equation (1) is linear in $f$; so if some functions $f_{1}$ and $f_{2}$ satisfy (1) and $c_{1}, c_{2}$ are real numbers, then $c_{1} f_{1}(x)+c_{2} f_{2}(x)$ is also a solution of (1). In order to make our formulas simpler, define $$ f_{0}(x)=f(x)-f(1) \\cdot x \\text {. } $$ This function is another one satisfying (1) and the extra constraint $f_{0}(1)=0$. Repeating the same argument on linear recurrences, we can write $f_{0}(a)=K(a) a^{n}+\\frac{L(a)}{a^{n}}$ with some functions $K$ and $L$. By substituting $n=0$, we can see that $K(a)+L(a)=f_{0}(1)=0$ for every $a$. Hence, $$ f_{0}\\left(a^{n}\\right)=K(a)\\left(a^{n}-\\frac{1}{a^{n}}\\right) $$ Now take two numbers $a>b>1$ arbitrarily and substitute $x=(a / b)^{n}$ and $y=(a b)^{n}$ in (1): $$ \\begin{aligned} \\left(\\frac{a^{n}}{b^{n}}+\\frac{b^{n}}{a^{n}}\\right) f_{0}\\left((a b)^{n}\\right) & =f_{0}\\left(a^{2 n}\\right)+f_{0}\\left(b^{2 n}\\right), \\quad \\text { so } \\\\ \\left(\\frac{a^{n}}{b^{n}}+\\frac{b^{n}}{a^{n}}\\right) K(a b)\\left((a b)^{n}-\\frac{1}{(a b)^{n}}\\right) & =K(a)\\left(a^{2 n}-\\frac{1}{a^{2 n}}\\right)+K(b)\\left(b^{2 n}-\\frac{1}{b^{2 n}}\\right), \\quad \\text { or equivalently } \\\\ K(a b)\\left(a^{2 n}-\\frac{1}{a^{2 n}}+b^{2 n}-\\frac{1}{b^{2 n}}\\right) & =K(a)\\left(a^{2 n}-\\frac{1}{a^{2 n}}\\right)+K(b)\\left(b^{2 n}-\\frac{1}{b^{2 n}}\\right) . \\end{aligned} $$ By dividing (5) by $a^{2 n}$ and then taking limit with $n \\rightarrow+\\infty$ we get $K(a b)=K(a)$. Then (5) reduces to $K(a)=K(b)$. Hence, $K(a)=K(b)$ for all $a>b>1$. Fix $a>1$. For every $x>0$ there is some $b$ and an integer $n$ such that $1<b<a$ and $x=b^{n}$. Then $$ f_{0}(x)=f_{0}\\left(b^{n}\\right)=K(b)\\left(b^{n}-\\frac{1}{b^{n}}\\right)=K(a)\\left(x-\\frac{1}{x}\\right) . $$ Hence, we have $f(x)=f_{0}(x)+f(1) x=C_{1} x+\\frac{C_{2}}{x}$ with $C_{1}=K(a)+f(1)$ and $C_{2}=-K(a)$. Comment. After establishing (5), there are several variants of finishing the solution. For example, instead of taking a limit, we can obtain a system of linear equations for $K(a), K(b)$ and $K(a b)$ by substituting two positive integers $n$ in (5), say $n=1$ and $n=2$. This approach leads to a similar ending as in the first solution. Optionally, we define another function $f_{1}(x)=f_{0}(x)-C\\left(x-\\frac{1}{x}\\right)$ and prescribe $K(c)=0$ for another fixed $c$. Then we can choose $a b=c$ and decrease the number of terms in (5).", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A6", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $m, n \\geqslant 2$ be integers. Let $f\\left(x_{1}, \\ldots, x_{n}\\right)$ be a polynomial with real coefficients such that $$ f\\left(x_{1}, \\ldots, x_{n}\\right)=\\left\\lfloor\\frac{x_{1}+\\ldots+x_{n}}{m}\\right\\rfloor \\text { for every } x_{1}, \\ldots, x_{n} \\in\\{0,1, \\ldots, m-1\\} $$ Prove that the total degree of $f$ is at least $n$. (Brazil)", "solution": "We transform the problem to a single variable question by the following Lemma. Let $a_{1}, \\ldots, a_{n}$ be nonnegative integers and let $G(x)$ be a nonzero polynomial with $\\operatorname{deg} G \\leqslant a_{1}+\\ldots+a_{n}$. Suppose that some polynomial $F\\left(x_{1}, \\ldots, x_{n}\\right)$ satisfies $$ F\\left(x_{1}, \\ldots, x_{n}\\right)=G\\left(x_{1}+\\ldots+x_{n}\\right) \\quad \\text { for }\\left(x_{1}, \\ldots, x_{n}\\right) \\in\\left\\{0,1, \\ldots, a_{1}\\right\\} \\times \\ldots \\times\\left\\{0,1, \\ldots, a_{n}\\right\\} $$ Then $F$ cannot be the zero polynomial, and $\\operatorname{deg} F \\geqslant \\operatorname{deg} G$. For proving the lemma, we will use forward differences of polynomials. If $p(x)$ is a polynomial with a single variable, then define $(\\Delta p)(x)=p(x+1)-p(x)$. It is well-known that if $p$ is a nonconstant polynomial then $\\operatorname{deg} \\Delta p=\\operatorname{deg} p-1$. If $p\\left(x_{1}, \\ldots, x_{n}\\right)$ is a polynomial with $n$ variables and $1 \\leqslant k \\leqslant n$ then let $$ \\left(\\Delta_{k} p\\right)\\left(x_{1}, \\ldots, x_{n}\\right)=p\\left(x_{1}, \\ldots, x_{k-1}, x_{k}+1, x_{k+1}, \\ldots, x_{n}\\right)-p\\left(x_{1}, \\ldots, x_{n}\\right) . $$ It is also well-known that either $\\Delta_{k} p$ is the zero polynomial or $\\operatorname{deg}\\left(\\Delta_{k} p\\right) \\leqslant \\operatorname{deg} p-1$. Proof of the lemma. We apply induction on the degree of $G$. If $G$ is a constant polynomial then we have $F(0, \\ldots, 0)=G(0) \\neq 0$, so $F$ cannot be the zero polynomial. Suppose that $\\operatorname{deg} G \\geqslant 1$ and the lemma holds true for lower degrees. Since $a_{1}+\\ldots+a_{n} \\geqslant$ $\\operatorname{deg} G>0$, at least one of $a_{1}, \\ldots, a_{n}$ is positive; without loss of generality suppose $a_{1} \\geqslant 1$. Consider the polynomials $F_{1}=\\Delta_{1} F$ and $G_{1}=\\Delta G$. On the grid $\\left\\{0, \\ldots, a_{1}-1\\right\\} \\times\\left\\{0, \\ldots, a_{2}\\right\\} \\times$ $\\ldots \\times\\left\\{0, \\ldots, a_{n}\\right\\}$ we have $$ \\begin{aligned} F_{1}\\left(x_{1}, \\ldots, x_{n}\\right) & =F\\left(x_{1}+1, x_{2}, \\ldots, x_{n}\\right)-F\\left(x_{1}, x_{2}, \\ldots, x_{n}\\right)= \\\\ & =G\\left(x_{1}+\\ldots+x_{n}+1\\right)-G\\left(x_{1}+\\ldots+x_{n}\\right)=G_{1}\\left(x_{1}+\\ldots+x_{n}\\right) . \\end{aligned} $$ Since $G$ is nonconstant, we have $\\operatorname{deg} G_{1}=\\operatorname{deg} G-1 \\leqslant\\left(a_{1}-1\\right)+a_{2}+\\ldots+a_{n}$. Therefore we can apply the induction hypothesis to $F_{1}$ and $G_{1}$ and conclude that $F_{1}$ is not the zero polynomial and $\\operatorname{deg} F_{1} \\geqslant \\operatorname{deg} G_{1}$. Hence, $\\operatorname{deg} F \\geqslant \\operatorname{deg} F_{1}+1 \\geqslant \\operatorname{deg} G_{1}+1=\\operatorname{deg} G$. That finishes the proof. To prove the problem statement, take the unique polynomial $g(x)$ so that $g(x)=\\left\\lfloor\\frac{x}{m}\\right\\rfloor$ for $x \\in\\{0,1, \\ldots, n(m-1)\\}$ and $\\operatorname{deg} g \\leqslant n(m-1)$. Notice that precisely $n(m-1)+1$ values of $g$ are prescribed, so $g(x)$ indeed exists and is unique. Notice further that the constraints $g(0)=g(1)=0$ and $g(m)=1$ together enforce $\\operatorname{deg} g \\geqslant 2$. By applying the lemma to $a_{1}=\\ldots=a_{n}=m-1$ and the polynomials $f$ and $g$, we achieve $\\operatorname{deg} f \\geqslant \\operatorname{deg} g$. Hence we just need a suitable lower bound on $\\operatorname{deg} g$. Consider the polynomial $h(x)=g(x+m)-g(x)-1$. The degree of $g(x+m)-g(x)$ is $\\operatorname{deg} g-1 \\geqslant 1$, so $\\operatorname{deg} h=\\operatorname{deg} g-1 \\geqslant 1$, and therefore $h$ cannot be the zero polynomial. On the other hand, $h$ vanishes at the points $0,1, \\ldots, n(m-1)-m$, so $h$ has at least $(n-1)(m-1)$ roots. Hence, $$ \\operatorname{deg} f \\geqslant \\operatorname{deg} g=\\operatorname{deg} h+1 \\geqslant(n-1)(m-1)+1 \\geqslant n $$ Comment 1. In the lemma we have equality for the choice $F\\left(x_{1}, \\ldots, x_{n}\\right)=G\\left(x_{1}+\\ldots+x_{n}\\right)$, so it indeed transforms the problem to an equivalent single-variable question. Comment 2. If $m \\geqslant 3$, the polynomial $h(x)$ can be replaced by $\\Delta g$. Notice that $$ (\\Delta g)(x)= \\begin{cases}1 & \\text { if } x \\equiv-1 \\quad(\\bmod m) \\quad \\text { for } x=0,1, \\ldots, n(m-1)-1 \\\\ 0 & \\text { otherwise }\\end{cases} $$ Hence, $\\Delta g$ vanishes at all integers $x$ with $0 \\leqslant x<n(m-1)$ and $x \\not \\equiv-1(\\bmod m)$. This leads to $\\operatorname{deg} g \\geqslant \\frac{(m-1)^{2} n}{m}+1$. If $m$ is even then this lower bound can be improved to $n(m-1)$. For $0 \\leqslant N<n(m-1)$, the $(N+1)^{\\text {st }}$ forward difference at $x=0$ is $$ \\left(\\Delta^{N+1}\\right) g(0)=\\sum_{k=0}^{N}(-1)^{N-k}\\left(\\begin{array}{c} N \\\\ k \\end{array}\\right)(\\Delta g)(k)=\\sum_{\\substack{0 \\leqslant k \\leqslant N \\\\ k \\equiv-1(\\bmod m)}}(-1)^{N-k}\\left(\\begin{array}{c} N \\\\ k \\end{array}\\right) $$ Since $m$ is even, all signs in the last sum are equal; with $N=n(m-1)-1$ this proves $\\Delta^{n(m-1)} g(0) \\neq 0$, indicating that $\\operatorname{deg} g \\geqslant n(m-1)$. However, there are infinitely many cases when all terms in (*) cancel out, for example if $m$ is an odd divisor of $n+1$. In such cases, $\\operatorname{deg} f$ can be less than $n(m-1)$. Comment 3. The lemma is closely related to the so-called Alon-Füredi bound. Let $S_{1}, \\ldots, S_{n}$ be nonempty finite sets in a field and suppose that the polynomial $P\\left(x_{1}, \\ldots, x_{n}\\right)$ vanishes at the points of the grid $S_{1} \\times \\ldots \\times S_{n}$, except for a single point. Then $\\operatorname{deg} P \\geqslant \\sum_{i=1}^{n}\\left(\\left|S_{i}\\right|-1\\right)$. (A well-known application of the Alon-Füredi bound was the former IMO problem 2007/6. Since then, this result became popular among the students and is part of the IMO training for many IMO teams.) The proof of the lemma can be replaced by an application of the Alon-Füredi bound as follows. Let $d=\\operatorname{deg} G$, and let $G_{0}$ be the unique polynomial such that $G_{0}(x)=G(x)$ for $x \\in\\{0,1, \\ldots, d-1\\}$ but $\\operatorname{deg} G_{0}<d$. The polynomials $G_{0}$ and $G$ are different because they have different degrees, and they attain the same values at $0,1, \\ldots, d-1$; that enforces $G_{0}(d) \\neq G(d)$. Choose some nonnegative integers $b_{1}, \\ldots, b_{n}$ so that $b_{1} \\leqslant a_{1}, \\ldots, b_{n} \\leqslant a_{n}$, and $b_{1}+\\ldots+b_{n}=d$, and consider the polynomial $$ H\\left(x_{1}, \\ldots, x_{n}\\right)=F\\left(x_{1}, \\ldots, x_{n}\\right)-G_{0}\\left(x_{1}+\\ldots+x_{n}\\right) $$ on the grid $\\left\\{0,1, \\ldots, b_{1}\\right\\} \\times \\ldots \\times\\left\\{0,1, \\ldots, b_{n}\\right\\}$. At the point $\\left(b_{1}, \\ldots, b_{n}\\right)$ we have $H\\left(b_{1}, \\ldots, b_{n}\\right)=G(d)-G_{0}(d) \\neq 0$. At all other points of the grid we have $F=G$ and therefore $H=G-G_{0}=0$. So, by the Alon-Füredi bound, $\\operatorname{deg} H \\geqslant b_{1}+\\ldots+b_{n}=d$. Since $\\operatorname{deg} G_{0}<d$, this implies $\\operatorname{deg} F=\\operatorname{deg}\\left(H+G_{0}\\right)=\\operatorname{deg} H \\geqslant d=\\operatorname{deg} G$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A7", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find the maximal value of $$ S=\\sqrt[3]{\\frac{a}{b+7}}+\\sqrt[3]{\\frac{b}{c+7}}+\\sqrt[3]{\\frac{c}{d+7}}+\\sqrt[3]{\\frac{d}{a+7}} $$ where $a, b, c, d$ are nonnegative real numbers which satisfy $a+b+c+d=100$.", "solution": "Since the value $8 / \\sqrt[3]{7}$ is reached, it suffices to prove that $S \\leqslant 8 / \\sqrt[3]{7}$. Assume that $x, y, z, t$ is a permutation of the variables, with $x \\leqslant y \\leqslant z \\leqslant t$. Then, by the rearrangement inequality, $$ S \\leqslant\\left(\\sqrt[3]{\\frac{x}{t+7}}+\\sqrt[3]{\\frac{t}{x+7}}\\right)+\\left(\\sqrt[3]{\\frac{y}{z+7}}+\\sqrt[3]{\\frac{z}{y+7}}\\right) $$ Claim. The first bracket above does not exceed $\\sqrt[3]{\\frac{x+t+14}{7}}$. Proof. Since $$ X^{3}+Y^{3}+3 X Y Z-Z^{3}=\\frac{1}{2}(X+Y-Z)\\left((X-Y)^{2}+(X+Z)^{2}+(Y+Z)^{2}\\right) $$ the inequality $X+Y \\leqslant Z$ is equivalent (when $X, Y, Z \\geqslant 0$ ) to $X^{3}+Y^{3}+3 X Y Z \\leqslant Z^{3}$. Therefore, the claim is equivalent to $$ \\frac{x}{t+7}+\\frac{t}{x+7}+3 \\sqrt[3]{\\frac{x t(x+t+14)}{7(x+7)(t+7)}} \\leqslant \\frac{x+t+14}{7} $$ Notice that $$ \\begin{array}{r} 3 \\sqrt[3]{\\frac{x t(x+t+14)}{7(x+7)(t+7)}}=3 \\sqrt[3]{\\frac{t(x+7)}{7(t+7)} \\cdot \\frac{x(t+7)}{7(x+7)} \\cdot \\frac{7(x+t+14)}{(t+7)(x+7)}} \\\\ \\leqslant \\frac{t(x+7)}{7(t+7)}+\\frac{x(t+7)}{7(x+7)}+\\frac{7(x+t+14)}{(t+7)(x+7)} \\end{array} $$ by the AM-GM inequality, so it suffices to prove $$ \\frac{x}{t+7}+\\frac{t}{x+7}+\\frac{t(x+7)}{7(t+7)}+\\frac{x(t+7)}{7(x+7)}+\\frac{7(x+t+14)}{(t+7)(x+7)} \\leqslant \\frac{x+t+14}{7} . $$ A straightforward check verifies that the last inequality is in fact an equality. The claim leads now to $$ S \\leqslant \\sqrt[3]{\\frac{x+t+14}{7}}+\\sqrt[3]{\\frac{y+z+14}{7}} \\leqslant 2 \\sqrt[3]{\\frac{x+y+z+t+28}{14}}=\\frac{8}{\\sqrt[3]{7}} $$ the last inequality being due to the AM-CM inequality (or to the fact that $\\sqrt[3]{ }$ is concave on $[0, \\infty))$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A7", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find the maximal value of $$ S=\\sqrt[3]{\\frac{a}{b+7}}+\\sqrt[3]{\\frac{b}{c+7}}+\\sqrt[3]{\\frac{c}{d+7}}+\\sqrt[3]{\\frac{d}{a+7}} $$ where $a, b, c, d$ are nonnegative real numbers which satisfy $a+b+c+d=100$.", "solution": "We present a different proof for the estimate $S \\leqslant 8 / \\sqrt[3]{7}$. Start by using Hölder's inequality: $$ S^{3}=\\left(\\sum_{\\mathrm{cyc}} \\frac{\\sqrt[6]{a} \\cdot \\sqrt[6]{a}}{\\sqrt[3]{b+7}}\\right)^{3} \\leqslant \\sum_{\\mathrm{cyc}}(\\sqrt[6]{a})^{3} \\cdot \\sum_{\\mathrm{cyc}}(\\sqrt[6]{a})^{3} \\cdot \\sum_{\\mathrm{cyc}}\\left(\\frac{1}{\\sqrt[3]{b+7}}\\right)^{3}=\\left(\\sum_{\\mathrm{cyc}} \\sqrt{a}\\right)^{2} \\sum_{\\mathrm{cyc}} \\frac{1}{b+7} $$ Notice that $$ \\frac{(x-1)^{2}(x-7)^{2}}{x^{2}+7} \\geqslant 0 \\Longleftrightarrow x^{2}-16 x+71 \\geqslant \\frac{448}{x^{2}+7} $$ yields $$ \\sum \\frac{1}{b+7} \\leqslant \\frac{1}{448} \\sum(b-16 \\sqrt{b}+71)=\\frac{1}{448}\\left(384-16 \\sum \\sqrt{b}\\right)=\\frac{48-2 \\sum \\sqrt{b}}{56} $$ Finally, $$ S^{3} \\leqslant \\frac{1}{56}\\left(\\sum \\sqrt{a}\\right)^{2}\\left(48-2 \\sum \\sqrt{a}\\right) \\leqslant \\frac{1}{56}\\left(\\frac{\\sum \\sqrt{a}+\\sum \\sqrt{a}+\\left(48-2 \\sum \\sqrt{a}\\right)}{3}\\right)^{3}=\\frac{512}{7} $$ by the AM-GM inequality. The conclusion follows. Comment. All the above works if we replace 7 and 100 with $k>0$ and $2\\left(k^{2}+1\\right)$, respectively; in this case, the answer becomes $$ 2 \\sqrt[3]{\\frac{(k+1)^{2}}{k}} $$ Even further, a linear substitution allows to extend the solutions to a version with 7 and 100 being replaced with arbitrary positive real numbers $p$ and $q$ satisfying $q \\geqslant 4 p$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C1", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $n \\geqslant 3$ be an integer. Prove that there exists a set $S$ of $2 n$ positive integers satisfying the following property: For every $m=2,3, \\ldots, n$ the set $S$ can be partitioned into two subsets with equal sums of elements, with one of subsets of cardinality $m$. (Iceland)", "solution": "We show that one of possible examples is the set $$ S=\\left\\{1 \\cdot 3^{k}, 2 \\cdot 3^{k}: k=1,2, \\ldots, n-1\\right\\} \\cup\\left\\{1, \\frac{3^{n}+9}{2}-1\\right\\} $$ It is readily verified that all the numbers listed above are distinct (notice that the last two are not divisible by 3 ). The sum of elements in $S$ is $$ \\Sigma=1+\\left(\\frac{3^{n}+9}{2}-1\\right)+\\sum_{k=1}^{n-1}\\left(1 \\cdot 3^{k}+2 \\cdot 3^{k}\\right)=\\frac{3^{n}+9}{2}+\\sum_{k=1}^{n-1} 3^{k+1}=\\frac{3^{n}+9}{2}+\\frac{3^{n+1}-9}{2}=2 \\cdot 3^{n} $$ Hence, in order to show that this set satisfies the problem requirements, it suffices to present, for every $m=2,3, \\ldots, n$, an $m$-element subset $A_{m} \\subset S$ whose sum of elements equals $3^{n}$. Such a subset is $$ A_{m}=\\left\\{2 \\cdot 3^{k}: k=n-m+1, n-m+2, \\ldots, n-1\\right\\} \\cup\\left\\{1 \\cdot 3^{n-m+1}\\right\\} . $$ Clearly, $\\left|A_{m}\\right|=m$. The sum of elements in $A_{m}$ is $$ 3^{n-m+1}+\\sum_{k=n-m+1}^{n-1} 2 \\cdot 3^{k}=3^{n-m+1}+\\frac{2 \\cdot 3^{n}-2 \\cdot 3^{n-m+1}}{2}=3^{n} $$ as required. Comment. Let us present a more general construction. Let $s_{1}, s_{2}, \\ldots, s_{2 n-1}$ be a sequence of pairwise distinct positive integers satisfying $s_{2 i+1}=s_{2 i}+s_{2 i-1}$ for all $i=2,3, \\ldots, n-1$. Set $s_{2 n}=s_{1}+s_{2}+$ $\\cdots+s_{2 n-4}$. Assume that $s_{2 n}$ is distinct from the other terms of the sequence. Then the set $S=\\left\\{s_{1}, s_{2}, \\ldots, s_{2 n}\\right\\}$ satisfies the problem requirements. Indeed, the sum of its elements is $$ \\Sigma=\\sum_{i=1}^{2 n-4} s_{i}+\\left(s_{2 n-3}+s_{2 n-2}\\right)+s_{2 n-1}+s_{2 n}=s_{2 n}+s_{2 n-1}+s_{2 n-1}+s_{2 n}=2 s_{2 n}+2 s_{2 n-1} $$ Therefore, we have $$ \\frac{\\Sigma}{2}=s_{2 n}+s_{2 n-1}=s_{2 n}+s_{2 n-2}+s_{2 n-3}=s_{2 n}+s_{2 n-2}+s_{2 n-4}+s_{2 n-5}=\\ldots, $$ which shows that the required sets $A_{m}$ can be chosen as $$ A_{m}=\\left\\{s_{2 n}, s_{2 n-2}, \\ldots, s_{2 n-2 m+4}, s_{2 n-2 m+3}\\right\\} $$ So, the only condition to be satisfied is $s_{2 n} \\notin\\left\\{s_{1}, s_{2}, \\ldots, s_{2 n-1}\\right\\}$, which can be achieved in many different ways (e.g., by choosing properly the number $s_{1}$ after specifying $s_{2}, s_{3}, \\ldots, s_{2 n-1}$ ). The solution above is an instance of this general construction. Another instance, for $n>3$, is the set $$ \\left\\{F_{1}, F_{2}, \\ldots, F_{2 n-1}, F_{1}+\\cdots+F_{2 n-4}\\right\\}, $$ where $F_{1}=1, F_{2}=2, F_{n+1}=F_{n}+F_{n-1}$ is the usual Fibonacci sequence.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Queenie and Horst play a game on a $20 \\times 20$ chessboard. In the beginning the board is empty. In every turn, Horst places a black knight on an empty square in such a way that his new knight does not attack any previous knights. Then Queenie places a white queen on an empty square. The game gets finished when somebody cannot move. Find the maximal positive $K$ such that, regardless of the strategy of Queenie, Horst can put at least $K$ knights on the board. (Armenia)", "solution": "We show two strategies, one for Horst to place at least 100 knights, and another strategy for Queenie that prevents Horst from putting more than 100 knights on the board. A strategy for Horst: Put knights only on black squares, until all black squares get occupied. Colour the squares of the board black and white in the usual way, such that the white and black squares alternate, and let Horst put his knights on black squares as long as it is possible. Two knights on squares of the same colour never attack each other. The number of black squares is $20^{2} / 2=200$. The two players occupy the squares in turn, so Horst will surely find empty black squares in his first 100 steps. A strategy for Queenie: Group the squares into cycles of length 4, and after each step of Horst, occupy the opposite square in the same cycle. Consider the squares of the board as vertices of a graph; let two squares be connected if two knights on those squares would attack each other. Notice that in a $4 \\times 4$ board the squares can be grouped into 4 cycles of length 4 , as shown in Figure 1. Divide the board into parts of size $4 \\times 4$, and perform the same grouping in every part; this way we arrange the 400 squares of the board into 100 cycles (Figure 2).  Figure 1  Figure 2  Figure 3 The strategy of Queenie can be as follows: Whenever Horst puts a new knight to a certain square $A$, which is part of some cycle $A-B-C-D-A$, let Queenie put her queen on the opposite square $C$ in that cycle (Figure 3). From this point, Horst cannot put any knight on $A$ or $C$ because those squares are already occupied, neither on $B$ or $D$ because those squares are attacked by the knight standing on $A$. Hence, Horst can put at most one knight on each cycle, that is at most 100 knights in total. Comment 1. Queenie's strategy can be prescribed by a simple rule: divide the board into $4 \\times 4$ parts; whenever Horst puts a knight in a part $P$, Queenie reflects that square about the centre of $P$ and puts her queen on the reflected square. Comment 2. The result remains the same if Queenie moves first. In the first turn, she may put her first queen arbitrarily. Later, if she has to put her next queen on a square that already contains a queen, she may move arbitrarily again.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C3", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $n$ be a given positive integer. Sisyphus performs a sequence of turns on a board consisting of $n+1$ squares in a row, numbered 0 to $n$ from left to right. Initially, $n$ stones are put into square 0, and the other squares are empty. At every turn, Sisyphus chooses any nonempty square, say with $k$ stones, takes one of those stones and moves it to the right by at most $k$ squares (the stone should stay within the board). Sisyphus' aim is to move all $n$ stones to square $n$. Prove that Sisyphus cannot reach the aim in less than $$ \\left\\lceil\\frac{n}{1}\\right\\rceil+\\left\\lceil\\frac{n}{2}\\right\\rceil+\\left\\lceil\\frac{n}{3}\\right\\rceil+\\cdots+\\left\\lceil\\frac{n}{n}\\right\\rceil $$ turns. (As usual, $\\lceil x\\rceil$ stands for the least integer not smaller than $x$.) (Netherlands)", "solution": "The stones are indistinguishable, and all have the same origin and the same final position. So, at any turn we can prescribe which stone from the chosen square to move. We do it in the following manner. Number the stones from 1 to $n$. At any turn, after choosing a square, Sisyphus moves the stone with the largest number from this square. This way, when stone $k$ is moved from some square, that square contains not more than $k$ stones (since all their numbers are at most $k$ ). Therefore, stone $k$ is moved by at most $k$ squares at each turn. Since the total shift of the stone is exactly $n$, at least $\\lceil n / k\\rceil$ moves of stone $k$ should have been made, for every $k=1,2, \\ldots, n$. By summing up over all $k=1,2, \\ldots, n$, we get the required estimate. Comment. The original submission contained the second part, asking for which values of $n$ the equality can be achieved. The answer is $n=1,2,3,4,5,7$. The Problem Selection Committee considered this part to be less suitable for the competition, due to technicalities.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C4", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "An anti-Pascal pyramid is a finite set of numbers, placed in a triangle-shaped array so that the first row of the array contains one number, the second row contains two numbers, the third row contains three numbers and so on; and, except for the numbers in the bottom row, each number equals the absolute value of the difference of the two numbers below it. For instance, the triangle below is an anti-Pascal pyramid with four rows, in which every integer from 1 to $1+2+3+4=10$ occurs exactly once: $$ \\begin{array}{cccc} & & 4 \\\\ & 2 & 6 & \\\\ & 5 \\quad 7 \\quad 1 \\\\ 8 & 3 & 10 & 9 . \\end{array} $$ Is it possible to form an anti-Pascal pyramid with 2018 rows, using every integer from 1 to $1+2+\\cdots+2018$ exactly once? (Iran)", "solution": "Let $T$ be an anti-Pascal pyramid with $n$ rows, containing every integer from 1 to $1+2+\\cdots+n$, and let $a_{1}$ be the topmost number in $T$ (Figure 1). The two numbers below $a_{1}$ are some $a_{2}$ and $b_{2}=a_{1}+a_{2}$, the two numbers below $b_{2}$ are some $a_{3}$ and $b_{3}=a_{1}+a_{2}+a_{3}$, and so on and so forth all the way down to the bottom row, where some $a_{n}$ and $b_{n}=a_{1}+a_{2}+\\cdots+a_{n}$ are the two neighbours below $b_{n-1}=a_{1}+a_{2}+\\cdots+a_{n-1}$. Since the $a_{k}$ are $n$ pairwise distinct positive integers whose sum does not exceed the largest number in $T$, which is $1+2+\\cdots+n$, it follows that they form a permutation of $1,2, \\ldots, n$.  Figure 1  Figure 2 Consider now (Figure 2) the two 'equilateral' subtriangles of $T$ whose bottom rows contain the numbers to the left, respectively right, of the pair $a_{n}, b_{n}$. (One of these subtriangles may very well be empty.) At least one of these subtriangles, say $T^{\\prime}$, has side length $\\ell \\geqslant\\lceil(n-2) / 2\\rceil$. Since $T^{\\prime}$ obeys the anti-Pascal rule, it contains $\\ell$ pairwise distinct positive integers $a_{1}^{\\prime}, a_{2}^{\\prime}, \\ldots, a_{\\ell}^{\\prime}$, where $a_{1}^{\\prime}$ is at the apex, and $a_{k}^{\\prime}$ and $b_{k}^{\\prime}=a_{1}^{\\prime}+a_{2}^{\\prime}+\\cdots+a_{k}^{\\prime}$ are the two neighbours below $b_{k-1}^{\\prime}$ for each $k=2,3 \\ldots, \\ell$. Since the $a_{k}$ all lie outside $T^{\\prime}$, and they form a permutation of $1,2, \\ldots, n$, the $a_{k}^{\\prime}$ are all greater than $n$. Consequently, $$ \\begin{array}{r} b_{\\ell}^{\\prime} \\geqslant(n+1)+(n+2)+\\cdots+(n+\\ell)=\\frac{\\ell(2 n+\\ell+1)}{2} \\\\ \\geqslant \\frac{1}{2} \\cdot \\frac{n-2}{2}\\left(2 n+\\frac{n-2}{2}+1\\right)=\\frac{5 n(n-2)}{8}, \\end{array} $$ which is greater than $1+2+\\cdots+n=n(n+1) / 2$ for $n=2018$. A contradiction. Comment. The above estimate may be slightly improved by noticing that $b_{\\ell}^{\\prime} \\neq b_{n}$. This implies $n(n+1) / 2=b_{n}>b_{\\ell}^{\\prime} \\geqslant\\lceil(n-2) / 2\\rceil(2 n+\\lceil(n-2) / 2\\rceil+1) / 2$, so $n \\leqslant 7$ if $n$ is odd, and $n \\leqslant 12$ if $n$ is even. It seems that the largest anti-Pascal pyramid whose entries are a permutation of the integers from 1 to $1+2+\\cdots+n$ has 5 rows.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $k$ be a positive integer. The organising committee of a tennis tournament is to schedule the matches for $2 k$ players so that every two players play once, each day exactly one match is played, and each player arrives to the tournament site the day of his first match, and departs the day of his last match. For every day a player is present on the tournament, the committee has to pay 1 coin to the hotel. The organisers want to design the schedule so as to minimise the total cost of all players' stays. Determine this minimum cost. (Russia)", "solution": "Enumerate the days of the tournament $1,2, \\ldots,\\left(\\begin{array}{c}2 k \\\\ 2\\end{array}\\right)$. Let $b_{1} \\leqslant b_{2} \\leqslant \\cdots \\leqslant b_{2 k}$ be the days the players arrive to the tournament, arranged in nondecreasing order; similarly, let $e_{1} \\geqslant \\cdots \\geqslant e_{2 k}$ be the days they depart arranged in nonincreasing order (it may happen that a player arrives on day $b_{i}$ and departs on day $e_{j}$, where $i \\neq j$ ). If a player arrives on day $b$ and departs on day $e$, then his stay cost is $e-b+1$. Therefore, the total stay cost is $$ \\Sigma=\\sum_{i=1}^{2 k} e_{i}-\\sum_{i=1}^{2 k} b_{i}+n=\\sum_{i=1}^{2 k}\\left(e_{i}-b_{i}+1\\right) $$ Bounding the total cost from below. To this end, estimate $e_{i+1}-b_{i+1}+1$. Before day $b_{i+1}$, only $i$ players were present, so at most $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ matches could be played. Therefore, $b_{i+1} \\leqslant\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)+1$. Similarly, at most $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ matches could be played after day $e_{i+1}$, so $e_{i} \\geqslant\\left(\\begin{array}{c}2 k \\\\ 2\\end{array}\\right)-\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$. Thus, $$ e_{i+1}-b_{i+1}+1 \\geqslant\\left(\\begin{array}{c} 2 k \\\\ 2 \\end{array}\\right)-2\\left(\\begin{array}{l} i \\\\ 2 \\end{array}\\right)=k(2 k-1)-i(i-1) $$ This lower bound can be improved for $i>k$ : List the $i$ players who arrived first, and the $i$ players who departed last; at least $2 i-2 k$ players appear in both lists. The matches between these players were counted twice, though the players in each pair have played only once. Therefore, if $i>k$, then $$ e_{i+1}-b_{i+1}+1 \\geqslant\\left(\\begin{array}{c} 2 k \\\\ 2 \\end{array}\\right)-2\\left(\\begin{array}{c} i \\\\ 2 \\end{array}\\right)+\\left(\\begin{array}{c} 2 i-2 k \\\\ 2 \\end{array}\\right)=(2 k-i)^{2} $$ An optimal tournament, We now describe a schedule in which the lower bounds above are all achieved simultaneously. Split players into two groups $X$ and $Y$, each of cardinality $k$. Next, partition the schedule into three parts. During the first part, the players from $X$ arrive one by one, and each newly arrived player immediately plays with everyone already present. During the third part (after all players from $X$ have already departed) the players from $Y$ depart one by one, each playing with everyone still present just before departing. In the middle part, everyone from $X$ should play with everyone from $Y$. Let $S_{1}, S_{2}, \\ldots, S_{k}$ be the players in $X$, and let $T_{1}, T_{2}, \\ldots, T_{k}$ be the players in $Y$. Let $T_{1}, T_{2}, \\ldots, T_{k}$ arrive in this order; after $T_{j}$ arrives, he immediately plays with all the $S_{i}, i>j$. Afterwards, players $S_{k}$, $S_{k-1}, \\ldots, S_{1}$ depart in this order; each $S_{i}$ plays with all the $T_{j}, i \\leqslant j$, just before his departure, and $S_{k}$ departs the day $T_{k}$ arrives. For $0 \\leqslant s \\leqslant k-1$, the number of matches played between $T_{k-s}$ 's arrival and $S_{k-s}$ 's departure is $$ \\sum_{j=k-s}^{k-1}(k-j)+1+\\sum_{j=k-s}^{k-1}(k-j+1)=\\frac{1}{2} s(s+1)+1+\\frac{1}{2} s(s+3)=(s+1)^{2} $$ Thus, if $i>k$, then the number of matches that have been played between $T_{i-k+1}$ 's arrival, which is $b_{i+1}$, and $S_{i-k+1}$ 's departure, which is $e_{i+1}$, is $(2 k-i)^{2}$; that is, $e_{i+1}-b_{i+1}+1=(2 k-i)^{2}$, showing the second lower bound achieved for all $i>k$. If $i \\leqslant k$, then the matches between the $i$ players present before $b_{i+1}$ all fall in the first part of the schedule, so there are $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ such, and $b_{i+1}=\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)+1$. Similarly, after $e_{i+1}$, there are $i$ players left, all $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ matches now fall in the third part of the schedule, and $e_{i+1}=\\left(\\begin{array}{c}2 k \\\\ 2\\end{array}\\right)-\\left(\\begin{array}{c}i \\\\ 2\\end{array}\\right)$. The first lower bound is therefore also achieved for all $i \\leqslant k$. Consequently, all lower bounds are achieved simultaneously, and the schedule is indeed optimal. Evaluation. Finally, evaluate the total cost for the optimal schedule: $$ \\begin{aligned} \\Sigma & =\\sum_{i=0}^{k}(k(2 k-1)-i(i-1))+\\sum_{i=k+1}^{2 k-1}(2 k-i)^{2}=(k+1) k(2 k-1)-\\sum_{i=0}^{k} i(i-1)+\\sum_{j=1}^{k-1} j^{2} \\\\ & =k(k+1)(2 k-1)-k^{2}+\\frac{1}{2} k(k+1)=\\frac{1}{2} k\\left(4 k^{2}+k-1\\right) . \\end{aligned} $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $k$ be a positive integer. The organising committee of a tennis tournament is to schedule the matches for $2 k$ players so that every two players play once, each day exactly one match is played, and each player arrives to the tournament site the day of his first match, and departs the day of his last match. For every day a player is present on the tournament, the committee has to pay 1 coin to the hotel. The organisers want to design the schedule so as to minimise the total cost of all players' stays. Determine this minimum cost. (Russia)", "solution": "Consider any tournament schedule. Label players $P_{1}, P_{2}, \\ldots, P_{2 k}$ in order of their arrival, and label them again $Q_{2 k}, Q_{2 k-1}, \\ldots, Q_{1}$ in order of their departure, to define a permutation $a_{1}, a_{2}, \\ldots, a_{2 k}$ of $1,2, \\ldots, 2 k$ by $P_{i}=Q_{a_{i}}$. We first describe an optimal tournament for any given permutation $a_{1}, a_{2}, \\ldots, a_{2 k}$ of the indices $1,2, \\ldots, 2 k$. Next, we find an optimal permutation and an optimal tournament. Optimisation for a fixed $a_{1}, \\ldots, a_{2 k}$. We say that the cost of the match between $P_{i}$ and $P_{j}$ is the number of players present at the tournament when this match is played. Clearly, the Committee pays for each day the cost of the match of that day. Hence, we are to minimise the total cost of all matches. Notice that $Q_{2 k}$ 's departure does not precede $P_{2 k}$ 's arrival. Hence, the number of players at the tournament monotonically increases (non-strictly) until it reaches $2 k$, and then monotonically decreases (non-strictly). So, the best time to schedule the match between $P_{i}$ and $P_{j}$ is either when $P_{\\max (i, j)}$ arrives, or when $Q_{\\max \\left(a_{i}, a_{j}\\right)}$ departs, in which case the cost is $\\min \\left(\\max (i, j), \\max \\left(a_{i}, a_{j}\\right)\\right)$. Conversely, assuming that $i>j$, if this match is scheduled between the arrivals of $P_{i}$ and $P_{i+1}$, then its cost will be exactly $i=\\max (i, j)$. Similarly, one can make it cost $\\max \\left(a_{i}, a_{j}\\right)$. Obviously, these conditions can all be simultaneously satisfied, so the minimal cost for a fixed sequence $a_{1}, a_{2}, \\ldots, a_{2 k}$ is $$ \\Sigma\\left(a_{1}, \\ldots, a_{2 k}\\right)=\\sum_{1 \\leqslant i<j \\leqslant 2 k} \\min \\left(\\max (i, j), \\max \\left(a_{i}, a_{j}\\right)\\right) $$ Optimising the sequence $\\left(a_{i}\\right)$. Optimisation hinges on the lemma below. Lemma. If $a \\leqslant b$ and $c \\leqslant d$, then $$ \\begin{aligned} \\min (\\max (a, x), \\max (c, y))+\\min & (\\max (b, x), \\max (d, y)) \\\\ & \\geqslant \\min (\\max (a, x), \\max (d, y))+\\min (\\max (b, x), \\max (c, y)) \\end{aligned} $$ Proof. Write $a^{\\prime}=\\max (a, x) \\leqslant \\max (b, x)=b^{\\prime}$ and $c^{\\prime}=\\max (c, y) \\leqslant \\max (d, y)=d^{\\prime}$ and check that $\\min \\left(a^{\\prime}, c^{\\prime}\\right)+\\min \\left(b^{\\prime}, d^{\\prime}\\right) \\geqslant \\min \\left(a^{\\prime}, d^{\\prime}\\right)+\\min \\left(b^{\\prime}, c^{\\prime}\\right)$. Consider a permutation $a_{1}, a_{2}, \\ldots, a_{2 k}$ such that $a_{i}<a_{j}$ for some $i<j$. Swapping $a_{i}$ and $a_{j}$ does not change the $(i, j)$ th summand in (1), and for $\\ell \\notin\\{i, j\\}$ the sum of the $(i, \\ell)$ th and the $(j, \\ell)$ th summands does not increase by the Lemma. Hence the optimal value does not increase, but the number of disorders in the permutation increases. This process stops when $a_{i}=2 k+1-i$ for all $i$, so the required minimum is $$ \\begin{aligned} S(2 k, 2 k-1, \\ldots, 1) & =\\sum_{1 \\leqslant i<j \\leqslant 2 k} \\min (\\max (i, j), \\max (2 k+1-i, 2 k+1-j)) \\\\ & =\\sum_{1 \\leqslant i<j \\leqslant 2 k} \\min (j, 2 k+1-i) . \\end{aligned} $$ The latter sum is fairly tractable and yields the stated result; we omit the details. Comment. If the number of players is odd, say, $2 k-1$, the required minimum is $k(k-1)(4 k-1) / 2$. In this case, $|X|=k,|Y|=k-1$, the argument goes along the same lines, but some additional technicalities are to be taken care of. This page is intentionally left blank", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C6", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $a$ and $b$ be distinct positive integers. The following infinite process takes place on an initially empty board. (i) If there is at least a pair of equal numbers on the board, we choose such a pair and increase one of its components by $a$ and the other by $b$. (ii) If no such pair exists, we write down two times the number 0 . Prove that, no matter how we make the choices in $(i)$, operation (ii) will be performed only finitely many times. (Serbia)", "solution": "We may assume $\\operatorname{gcd}(a, b)=1$; otherwise we work in the same way with multiples of $d=\\operatorname{gcd}(a, b)$. Suppose that after $N$ moves of type (ii) and some moves of type $(i)$ we have to add two new zeros. For each integer $k$, denote by $f(k)$ the number of times that the number $k$ appeared on the board up to this moment. Then $f(0)=2 N$ and $f(k)=0$ for $k<0$. Since the board contains at most one $k-a$, every second occurrence of $k-a$ on the board produced, at some moment, an occurrence of $k$; the same stands for $k-b$. Therefore, $$ f(k)=\\left\\lfloor\\frac{f(k-a)}{2}\\right\\rfloor+\\left\\lfloor\\frac{f(k-b)}{2}\\right\\rfloor $$ yielding $$ f(k) \\geqslant \\frac{f(k-a)+f(k-b)}{2}-1 $$ Since $\\operatorname{gcd}(a, b)=1$, every integer $x>a b-a-b$ is expressible in the form $x=s a+t b$, with integer $s, t \\geqslant 0$. We will prove by induction on $s+t$ that if $x=s a+b t$, with $s, t$ nonnegative integers, then $$ f(x)>\\frac{f(0)}{2^{s+t}}-2 . $$ The base case $s+t=0$ is trivial. Assume now that (3) is true for $s+t=v$. Then, if $s+t=v+1$ and $x=s a+t b$, at least one of the numbers $s$ and $t$ - say $s$ - is positive, hence by (2), $$ f(x)=f(s a+t b) \\geqslant \\frac{f((s-1) a+t b)}{2}-1>\\frac{1}{2}\\left(\\frac{f(0)}{2^{s+t-1}}-2\\right)-1=\\frac{f(0)}{2^{s+t}}-2 . $$ Assume now that we must perform moves of type (ii) ad infinitum. Take $n=a b-a-b$ and suppose $b>a$. Since each of the numbers $n+1, n+2, \\ldots, n+b$ can be expressed in the form $s a+t b$, with $0 \\leqslant s \\leqslant b$ and $0 \\leqslant t \\leqslant a$, after moves of type (ii) have been performed $2^{a+b+1}$ times and we have to add a new pair of zeros, each $f(n+k), k=1,2, \\ldots, b$, is at least 2 . In this case (1) yields inductively $f(n+k) \\geqslant 2$ for all $k \\geqslant 1$. But this is absurd: after a finite number of moves, $f$ cannot attain nonzero values at infinitely many points.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C6", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $a$ and $b$ be distinct positive integers. The following infinite process takes place on an initially empty board. (i) If there is at least a pair of equal numbers on the board, we choose such a pair and increase one of its components by $a$ and the other by $b$. (ii) If no such pair exists, we write down two times the number 0 . Prove that, no matter how we make the choices in $(i)$, operation (ii) will be performed only finitely many times. (Serbia)", "solution": "We start by showing that the result of the process in the problem does not depend on the way the operations are performed. For that purpose, it is convenient to modify the process a bit. Claim 1. Suppose that the board initially contains a finite number of nonnegative integers, and one starts performing type $(i)$ moves only. Assume that one had applied $k$ moves which led to a final arrangement where no more type (i) moves are possible. Then, if one starts from the same initial arrangement, performing type (i) moves in an arbitrary fashion, then the process will necessarily stop at the same final arrangement Proof. Throughout this proof, all moves are supposed to be of type (i). Induct on $k$; the base case $k=0$ is trivial, since no moves are possible. Assume now that $k \\geqslant 1$. Fix some canonical process, consisting of $k$ moves $M_{1}, M_{2}, \\ldots, M_{k}$, and reaching the final arrangement $A$. Consider any sample process $m_{1}, m_{2}, \\ldots$ starting with the same initial arrangement and proceeding as long as possible; clearly, it contains at least one move. We need to show that this process stops at $A$. Let move $m_{1}$ consist in replacing two copies of $x$ with $x+a$ and $x+b$. If move $M_{1}$ does the same, we may apply the induction hypothesis to the arrangement appearing after $m_{1}$. Otherwise, the canonical process should still contain at least one move consisting in replacing $(x, x) \\mapsto(x+a, x+b)$, because the initial arrangement contains at least two copies of $x$, while the final one contains at most one such. Let $M_{i}$ be the first such move. Since the copies of $x$ are indistinguishable and no other copy of $x$ disappeared before $M_{i}$ in the canonical process, the moves in this process can be permuted as $M_{i}, M_{1}, \\ldots, M_{i-1}, M_{i+1}, \\ldots, M_{k}$, without affecting the final arrangement. Now it suffices to perform the move $m_{1}=M_{i}$ and apply the induction hypothesis as above. Claim 2. Consider any process starting from the empty board, which involved exactly $n$ moves of type (ii) and led to a final arrangement where all the numbers are distinct. Assume that one starts with the board containing $2 n$ zeroes (as if $n$ moves of type (ii) were made in the beginning), applying type ( $i$ ) moves in an arbitrary way. Then this process will reach the same final arrangement. Proof. Starting with the board with $2 n$ zeros, one may indeed model the first process mentioned in the statement of the claim, omitting the type (ii) moves. This way, one reaches the same final arrangement. Now, Claim 1 yields that this final arrangement will be obtained when type (i) moves are applied arbitrarily. Claim 2 allows now to reformulate the problem statement as follows: There exists an integer $n$ such that, starting from $2 n$ zeroes, one may apply type (i) moves indefinitely. In order to prove this, we start with an obvious induction on $s+t=k \\geqslant 1$ to show that if we start with $2^{s+t}$ zeros, then we can get simultaneously on the board, at some point, each of the numbers $s a+t b$, with $s+t=k$. Suppose now that $a<b$. Then, an appropriate use of separate groups of zeros allows us to get two copies of each of the numbers $s a+t b$, with $1 \\leqslant s, t \\leqslant b$. Define $N=a b-a-b$, and notice that after representing each of numbers $N+k, 1 \\leqslant k \\leqslant b$, in the form $s a+t b, 1 \\leqslant s, t \\leqslant b$ we can get, using enough zeros, the numbers $N+1, N+2, \\ldots, N+a$ and the numbers $N+1, N+2, \\ldots, N+b$. From now on we can perform only moves of type ( $i$ ). Indeed, if $n \\geqslant N$, the occurrence of the numbers $n+1, n+2, \\ldots, n+a$ and $n+1, n+2, \\ldots, n+b$ and the replacement $(n+1, n+1) \\mapsto$ $(n+b+1, n+a+1)$ leads to the occurrence of the numbers $n+2, n+3, \\ldots, n+a+1$ and $n+2, n+3, \\ldots, n+b+1$. Comment. The proofs of Claims 1 and 2 may be extended in order to show that in fact the number of moves in the canonical process is the same as in an arbitrary sample one.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C7", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Consider 2018 pairwise crossing circles no three of which are concurrent. These circles subdivide the plane into regions bounded by circular edges that meet at vertices. Notice that there are an even number of vertices on each circle. Given the circle, alternately colour the vertices on that circle red and blue. In doing so for each circle, every vertex is coloured twice once for each of the two circles that cross at that point. If the two colourings agree at a vertex, then it is assigned that colour; otherwise, it becomes yellow. Show that, if some circle contains at least 2061 yellow points, then the vertices of some region are all yellow. (India)", "solution": "Letting $n=2018$, we will show that, if every region has at least one non-yellow vertex, then every circle contains at most $n+\\lfloor\\sqrt{n-2}\\rfloor-2$ yellow points. In the case at hand, the latter equals $2018+44-2=2060$, contradicting the hypothesis. Consider the natural geometric graph $G$ associated with the configuration of $n$ circles. Fix any circle $C$ in the configuration, let $k$ be the number of yellow points on $C$, and find a suitable lower bound for the total number of yellow vertices of $G$ in terms of $k$ and $n$. It turns out that $k$ is even, and $G$ has at least $$ k+2\\left(\\begin{array}{c} k / 2 \\\\ 2 \\end{array}\\right)+2\\left(\\begin{array}{c} n-k / 2-1 \\\\ 2 \\end{array}\\right)=\\frac{k^{2}}{2}-(n-2) k+(n-2)(n-1) $$ yellow vertices. The proof hinges on the two lemmata below. Lemma 1. Let two circles in the configuration cross at $x$ and $y$. Then $x$ and $y$ are either both yellow or both non-yellow. Proof. This is because the numbers of interior vertices on the four arcs $x$ and $y$ determine on the two circles have like parities. In particular, each circle in the configuration contains an even number of yellow vertices. Lemma 2. If $\\overrightarrow{x y}, \\overrightarrow{y z}$, and $\\overrightarrow{z x}$ are circular arcs of three pairwise distinct circles in the configuration, then the number of yellow vertices in the set $\\{x, y, z\\}$ is odd. Proof. Let $C_{1}, C_{2}, C_{3}$ be the three circles under consideration. Assume, without loss of generality, that $C_{2}$ and $C_{3}$ cross at $x, C_{3}$ and $C_{1}$ cross at $y$, and $C_{1}$ and $C_{2}$ cross at $z$. Let $k_{1}$, $k_{2}, k_{3}$ be the numbers of interior vertices on the three circular arcs under consideration. Since each circle in the configuration, different from the $C_{i}$, crosses the cycle $\\widehat{x y} \\cup \\widehat{y z} \\cup \\widehat{z x}$ at an even number of points (recall that no three circles are concurrent), and self-crossings are counted twice, the sum $k_{1}+k_{2}+k_{3}$ is even. Let $Z_{1}$ be the colour $z$ gets from $C_{1}$ and define the other colours similarly. By the preceding, the number of bichromatic pairs in the list $\\left(Z_{1}, Y_{1}\\right),\\left(X_{2}, Z_{2}\\right),\\left(Y_{3}, X_{3}\\right)$ is odd. Since the total number of colour changes in a cycle $Z_{1}-Y_{1}-Y_{3}-X_{3}-X_{2}-Z_{2}-Z_{1}$ is even, the number of bichromatic pairs in the list $\\left(X_{2}, X_{3}\\right),\\left(Y_{1}, Y_{3}\\right),\\left(Z_{1}, Z_{2}\\right)$ is odd, and the lemma follows. We are now in a position to prove that $(*)$ bounds the total number of yellow vertices from below. Refer to Lemma 1 to infer that the $k$ yellow vertices on $C$ pair off to form the pairs of points where $C$ is crossed by $k / 2$ circles in the configuration. By Lemma 2 , these circles cross pairwise to account for another $2\\left(\\begin{array}{c}k / 2 \\\\ 2\\end{array}\\right)$ yellow vertices. Finally, the remaining $n-k / 2-1$ circles in the configuration cross $C$ at non-yellow vertices, by Lemma 1, and Lemma 2 applies again to show that these circles cross pairwise to account for yet another $2\\left(\\begin{array}{c}n-k / 2-1 \\\\ 2\\end{array}\\right)$ yellow vertices. Consequently, there are at least (*) yellow vertices. Next, notice that $G$ is a plane graph on $n(n-1)$ degree 4 vertices, having exactly $2 n(n-1)$ edges and exactly $n(n-1)+2$ faces (regions), the outer face inclusive (by Euler's formula for planar graphs). Lemma 3. Each face of $G$ has equally many red and blue vertices. In particular, each face has an even number of non-yellow vertices. Proof. Trace the boundary of a face once in circular order, and consider the colours each vertex is assigned in the colouring of the two circles that cross at that vertex, to infer that colours of non-yellow vertices alternate. Consequently, if each region has at least one non-yellow vertex, then it has at least two such. Since each vertex of $G$ has degree 4, consideration of vertex-face incidences shows that $G$ has at least $n(n-1) / 2+1$ non-yellow vertices, and hence at most $n(n-1) / 2-1$ yellow vertices. (In fact, Lemma 3 shows that there are at least $n(n-1) / 4+1 / 2$ red, respectively blue, vertices.) Finally, recall the lower bound (*) for the total number of yellow vertices in $G$, to write $n(n-1) / 2-1 \\geqslant k^{2} / 2-(n-2) k+(n-2)(n-1)$, and conclude that $k \\leqslant n+\\lfloor\\sqrt{n-2}\\rfloor-2$, as claimed in the first paragraph.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C7", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Consider 2018 pairwise crossing circles no three of which are concurrent. These circles subdivide the plane into regions bounded by circular edges that meet at vertices. Notice that there are an even number of vertices on each circle. Given the circle, alternately colour the vertices on that circle red and blue. In doing so for each circle, every vertex is coloured twice once for each of the two circles that cross at that point. If the two colourings agree at a vertex, then it is assigned that colour; otherwise, it becomes yellow. Show that, if some circle contains at least 2061 yellow points, then the vertices of some region are all yellow. (India)", "solution": "The first two lemmata in Call the circles from the two classes white and black, respectively. Call a region yellow if its vertices are all yellow. Let $w$ and $b$ be the numbers of white and black circles, respectively; clearly, $w+b=n$. Assume that $w \\geqslant b$, and that there is no yellow region. Clearly, $b \\geqslant 1$, otherwise each region is yellow. The white circles subdivide the plane into $w(w-1)+2$ larger regions - call them white. The white regions (or rather their boundaries) subdivide each black circle into black arcs. Since there are no yellow regions, each white region contains at least one black arc. Consider any white region; let it contain $t \\geqslant 1$ black arcs. We claim that the number of points at which these $t$ arcs cross does not exceed $t-1$. To prove this, consider a multigraph whose vertices are these black arcs, two vertices being joined by an edge for each point at which the corresponding arcs cross. If this graph had more than $t-1$ edges, it would contain a cycle, since it has $t$ vertices; this cycle would correspond to a closed contour formed by black sub-arcs, lying inside the region under consideration. This contour would, in turn, define at least one yellow region, which is impossible. Let $t_{i}$ be the number of black arcs inside the $i^{\\text {th }}$ white region. The total number of black arcs is $\\sum_{i} t_{i}=2 w b$, and they cross at $2\\left(\\begin{array}{l}b \\\\ 2\\end{array}\\right)=b(b-1)$ points. By the preceding, $$ b(b-1) \\leqslant \\sum_{i=1}^{w^{2}-w+2}\\left(t_{i}-1\\right)=\\sum_{i=1}^{w^{2}-w+2} t_{i}-\\left(w^{2}-w+2\\right)=2 w b-\\left(w^{2}-w+2\\right) $$ or, equivalently, $(w-b)^{2} \\leqslant w+b-2=n-2$, which is the case if and only if $w-b \\leqslant\\lfloor\\sqrt{n-2}\\rfloor$. Consequently, $b \\leqslant w \\leqslant(n+\\lfloor\\sqrt{n-2}\\rfloor) / 2$, so there are at most $2(w-1) \\leqslant n+\\lfloor\\sqrt{n-2}\\rfloor-2$ yellow vertices on each circle - a contradiction.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G1", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be an acute-angled triangle with circumcircle $\\Gamma$. Let $D$ and $E$ be points on the segments $A B$ and $A C$, respectively, such that $A D=A E$. The perpendicular bisectors of the segments $B D$ and $C E$ intersect the small arcs $\\overparen{A B}$ and $\\overparen{A C}$ at points $F$ and $G$ respectively. Prove that $D E \\| F G$. (Greece)", "solution": "In the sequel, all the considered arcs are small arcs. Let $P$ be the midpoint of the $\\operatorname{arc} \\overparen{B C}$. Then $A P$ is the bisector of $\\angle B A C$, hence, in the isosceles triangle $A D E, A P \\perp D E$. So, the statement of the problem is equivalent to $A P \\perp F G$. In order to prove this, let $K$ be the second intersection of $\\Gamma$ with $F D$. Then the triangle $F B D$ is isosceles, therefore $$ \\angle A K F=\\angle A B F=\\angle F D B=\\angle A D K $$ yielding $A K=A D$. In the same way, denoting by $L$ the second intersection of $\\Gamma$ with $G E$, we get $A L=A E$. This shows that $A K=A L$.  Now $\\angle F B D=\\angle F D B$ gives $\\overparen{A F}=\\overparen{B F}+\\overparen{A K}=\\overparen{B F}+\\overparen{A L}$, hence $\\overparen{B F}=\\overparen{L F}$. In a similar way, we get $\\widehat{C G}=\\widehat{G K}$. This yields $$ \\angle(A P, F G)=\\frac{\\overparen{A F}+\\overparen{P G}}{2}=\\frac{\\overparen{A L}+\\overparen{L F}+\\overparen{P C}+\\overparen{C G}}{2}=\\frac{\\overparen{K L}+\\overparen{L B}+\\overparen{B C}+\\overparen{C K}}{4}=90^{\\circ} . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G1", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be an acute-angled triangle with circumcircle $\\Gamma$. Let $D$ and $E$ be points on the segments $A B$ and $A C$, respectively, such that $A D=A E$. The perpendicular bisectors of the segments $B D$ and $C E$ intersect the small arcs $\\overparen{A B}$ and $\\overparen{A C}$ at points $F$ and $G$ respectively. Prove that $D E \\| F G$. (Greece)", "solution": "Let $Z=A B \\cap F G, T=A C \\cap F G$. It suffices to prove that $\\angle A T Z=\\angle A Z T$. Let $X$ be the point for which $F X A D$ is a parallelogram. Then $$ \\angle F X A=\\angle F D A=180^{\\circ}-\\angle F D B=180^{\\circ}-\\angle F B D, $$ where in the last equality we used that $F D=F B$. It follows that the quadrilateral $B F X A$ is cyclic, so $X$ lies on $\\Gamma$.  Analogously, if $Y$ is the point for which $G Y A E$ is a parallelogram, then $Y$ lies on $\\Gamma$. So the quadrilateral $X F G Y$ is cyclic and $F X=A D=A E=G Y$, hence $X F G Y$ is an isosceles trapezoid. Now, by $X F \\| A Z$ and $Y G \\| A T$, it follows that $\\angle A T Z=\\angle Y G F=\\angle X F G=\\angle A Z T$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G1", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be an acute-angled triangle with circumcircle $\\Gamma$. Let $D$ and $E$ be points on the segments $A B$ and $A C$, respectively, such that $A D=A E$. The perpendicular bisectors of the segments $B D$ and $C E$ intersect the small arcs $\\overparen{A B}$ and $\\overparen{A C}$ at points $F$ and $G$ respectively. Prove that $D E \\| F G$. (Greece)", "solution": "As in the first solution, we prove that $F G \\perp A P$, where $P$ is the midpoint of the small arc $\\overparen{B C}$. Let $O$ be the circumcentre of the triangle $A B C$, and let $M$ and $N$ be the midpoints of the small arcs $\\overparen{A B}$ and $\\overparen{A C}$, respectively. Then $O M$ and $O N$ are the perpendicular bisectors of $A B$ and $A C$, respectively.  The distance $d$ between $O M$ and the perpendicular bisector of $B D$ is $\\frac{1}{2} A B-\\frac{1}{2} B D=\\frac{1}{2} A D$, hence it is equal to the distance between $O N$ and the perpendicular bisector of $C E$. This shows that the isosceles trapezoid determined by the diameter $\\delta$ of $\\Gamma$ through $M$ and the chord parallel to $\\delta$ through $F$ is congruent to the isosceles trapezoid determined by the diameter $\\delta^{\\prime}$ of $\\Gamma$ through $N$ and the chord parallel to $\\delta^{\\prime}$ through $G$. Therefore $M F=N G$, yielding $M N \\| F G$. Now $$ \\angle(M N, A P)=\\frac{1}{2}(\\overparen{A M}+\\overparen{P C}+\\overparen{C N})=\\frac{1}{4}(\\overparen{A B}+\\overparen{B C}+\\overparen{C A})=90^{\\circ} $$ hence $M N \\perp A P$, and the conclusion follows.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G2", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with $A B=A C$, and let $M$ be the midpoint of $B C$. Let $P$ be a point such that $P B<P C$ and $P A$ is parallel to $B C$. Let $X$ and $Y$ be points on the lines $P B$ and $P C$, respectively, so that $B$ lies on the segment $P X, C$ lies on the segment $P Y$, and $\\angle P X M=\\angle P Y M$. Prove that the quadrilateral $A P X Y$ is cyclic. (Australia)", "solution": "Since $A B=A C, A M$ is the perpendicular bisector of $B C$, hence $\\angle P A M=$ $\\angle A M C=90^{\\circ}$. 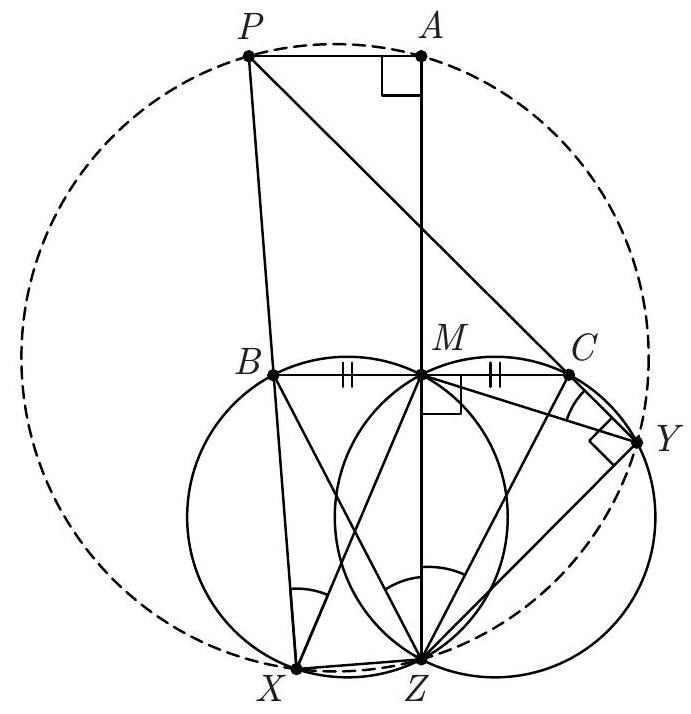 Now let $Z$ be the common point of $A M$ and the perpendicular through $Y$ to $P C$ (notice that $Z$ lies on to the ray $A M$ beyond $M$ ). We have $\\angle P A Z=\\angle P Y Z=90^{\\circ}$. Thus the points $P, A, Y$, and $Z$ are concyclic. Since $\\angle C M Z=\\angle C Y Z=90^{\\circ}$, the quadrilateral $C Y Z M$ is cyclic, hence $\\angle C Z M=$ $\\angle C Y M$. By the condition in the statement, $\\angle C Y M=\\angle B X M$, and, by symmetry in $Z M$, $\\angle C Z M=\\angle B Z M$. Therefore, $\\angle B X M=\\angle B Z M$. It follows that the points $B, X, Z$, and $M$ are concyclic, hence $\\angle B X Z=180^{\\circ}-\\angle B M Z=90^{\\circ}$. Finally, we have $\\angle P X Z=\\angle P Y Z=\\angle P A Z=90^{\\circ}$, hence the five points $P, A, X, Y, Z$ are concyclic. In particular, the quadrilateral $A P X Y$ is cyclic, as required. Comment 1. Clearly, the key point $Z$ from the solution above can be introduced in several different ways, e.g., as the second meeting point of the circle $C M Y$ and the line $A M$, or as the second meeting point of the circles $C M Y$ and $B M X$, etc. For some of definitions of $Z$ its location is not obvious. For instance, if $Z$ is defined as a common point of $A M$ and the perpendicular through $X$ to $P X$, it is not clear that $Z$ lies on the ray $A M$ beyond $M$. To avoid such slippery details some more restrictions on the construction may be required. Comment 2. Let us discuss a connection to the Miquel point of a cyclic quadrilateral. Set $X^{\\prime}=$ $M X \\cap P C, Y^{\\prime}=M Y \\cap P B$, and $Q=X Y \\cap X^{\\prime} Y^{\\prime}$ (see the figure below). We claim that $B C \\| P Q$. (One way of proving this is the following. Notice that the quadruple of lines $P X, P M, P Y, P Q$ is harmonic, hence the quadruple $B, M, C, P Q \\cap B C$ of their intersection points with $B C$ is harmonic. Since $M$ is the midpoint of $B C, P Q \\cap B C$ is an ideal point, i.e., $P Q \\| B C$.) It follows from the given equality $\\angle P X M=\\angle P Y M$ that the quadrilateral $X Y X^{\\prime} Y^{\\prime}$ is cyclic. Note that $A$ is the projection of $M$ onto $P Q$. By a known description, $A$ is the Miquel point for the sidelines $X Y, X Y^{\\prime}, X^{\\prime} Y, X^{\\prime} Y^{\\prime}$. In particular, the circle $P X Y$ passes through $A$. 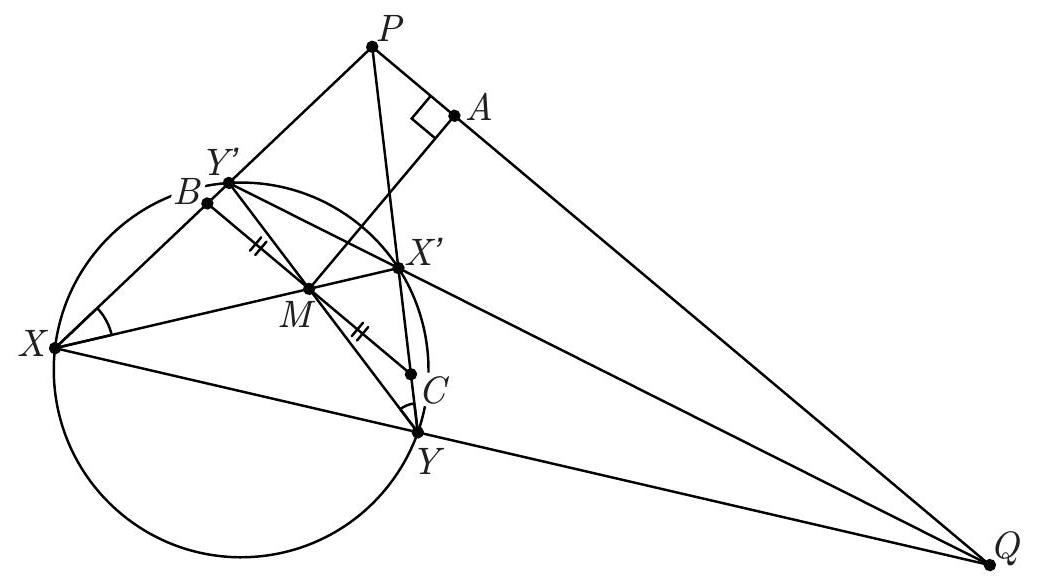 Comment 3. An alternative approach is the following. One can note that the (oriented) lengths of the segments $C Y$ and $B X$ are both linear functions of a parameter $t=\\cot \\angle P X M$. As $t$ varies, the intersection point $S$ of the perpendicular bisectors of $P X$ and $P Y$ traces a fixed line, thus the family of circles $P X Y$ has a fixed common point (other than $P$ ). By checking particular cases, one can show that this fixed point is $A$. Comment 4. The problem states that $\\angle P X M=\\angle P Y M$ implies that $A P X Y$ is cyclic. The original submission claims that these two conditions are in fact equivalent. The Problem Selection Committee omitted the converse part, since it follows easily from the direct one, by reversing arguments.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G3", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "A circle $\\omega$ of radius 1 is given. A collection $T$ of triangles is called good, if the following conditions hold: (i) each triangle from $T$ is inscribed in $\\omega$; (ii) no two triangles from $T$ have a common interior point. Determine all positive real numbers $t$ such that, for each positive integer $n$, there exists a good collection of $n$ triangles, each of perimeter greater than $t$. (South Africa)", "solution": "First, we show how to construct a good collection of $n$ triangles, each of perimeter greater than 4 . This will show that all $t \\leqslant 4$ satisfy the required conditions. Construct inductively an $(n+2)$-gon $B A_{1} A_{2} \\ldots A_{n} C$ inscribed in $\\omega$ such that $B C$ is a diameter, and $B A_{1} A_{2}, B A_{2} A_{3}, \\ldots, B A_{n-1} A_{n}, B A_{n} C$ is a good collection of $n$ triangles. For $n=1$, take any triangle $B A_{1} C$ inscribed in $\\omega$ such that $B C$ is a diameter; its perimeter is greater than $2 B C=4$. To perform the inductive step, assume that the $(n+2)$-gon $B A_{1} A_{2} \\ldots A_{n} C$ is already constructed. Since $A_{n} B+A_{n} C+B C>4$, one can choose a point $A_{n+1}$ on the small arc $\\widehat{C A_{n}}$, close enough to $C$, so that $A_{n} B+A_{n} A_{n+1}+B A_{n+1}$ is still greater than 4 . Thus each of these new triangles $B A_{n} A_{n+1}$ and $B A_{n+1} C$ has perimeter greater than 4, which completes the induction step. 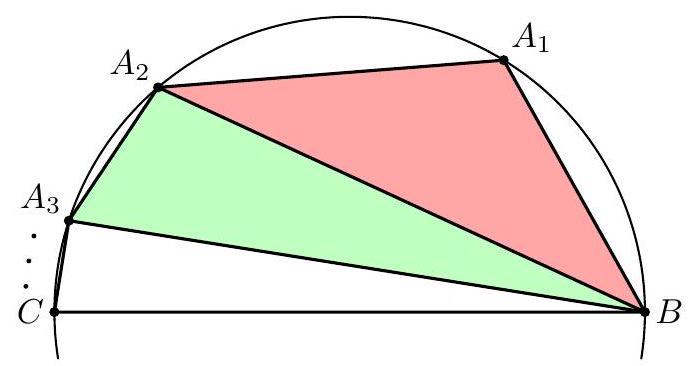 We proceed by showing that no $t>4$ satisfies the conditions of the problem. To this end, we assume that there exists a good collection $T$ of $n$ triangles, each of perimeter greater than $t$, and then bound $n$ from above. Take $\\varepsilon>0$ such that $t=4+2 \\varepsilon$. Claim. There exists a positive constant $\\sigma=\\sigma(\\varepsilon)$ such that any triangle $\\Delta$ with perimeter $2 s \\geqslant 4+2 \\varepsilon$, inscribed in $\\omega$, has area $S(\\Delta)$ at least $\\sigma$. Proof. Let $a, b, c$ be the side lengths of $\\Delta$. Since $\\Delta$ is inscribed in $\\omega$, each side has length at most 2. Therefore, $s-a \\geqslant(2+\\varepsilon)-2=\\varepsilon$. Similarly, $s-b \\geqslant \\varepsilon$ and $s-c \\geqslant \\varepsilon$. By Heron's formula, $S(\\Delta)=\\sqrt{s(s-a)(s-b)(s-c)} \\geqslant \\sqrt{(2+\\varepsilon) \\varepsilon^{3}}$. Thus we can set $\\sigma(\\varepsilon)=\\sqrt{(2+\\varepsilon) \\varepsilon^{3}}$. Now we see that the total area $S$ of all triangles from $T$ is at least $n \\sigma(\\varepsilon)$. On the other hand, $S$ does not exceed the area of the disk bounded by $\\omega$. Thus $n \\sigma(\\varepsilon) \\leqslant \\pi$, which means that $n$ is bounded from above. Comment 1. One may prove the Claim using the formula $S=\\frac{a b c}{4 R}$ instead of Heron's formula. Comment 2. In the statement of the problem condition $(i)$ could be replaced by a weaker one: each triangle from $T$ lies within $\\omega$. This does not affect the solution above, but reduces the number of ways to prove the Claim. This page is intentionally left blank", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G4", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "A point $T$ is chosen inside a triangle $A B C$. Let $A_{1}, B_{1}$, and $C_{1}$ be the reflections of $T$ in $B C, C A$, and $A B$, respectively. Let $\\Omega$ be the circumcircle of the triangle $A_{1} B_{1} C_{1}$. The lines $A_{1} T, B_{1} T$, and $C_{1} T$ meet $\\Omega$ again at $A_{2}, B_{2}$, and $C_{2}$, respectively. Prove that the lines $A A_{2}, B B_{2}$, and $C C_{2}$ are concurrent on $\\Omega$. (Mongolia)", "solution": "By $\\Varangle(\\ell, n)$ we always mean the directed angle of the lines $\\ell$ and $n$, taken modulo $180^{\\circ}$. Let $C C_{2}$ meet $\\Omega$ again at $K$ (as usual, if $C C_{2}$ is tangent to $\\Omega$, we set $T=C_{2}$ ). We show that the line $B B_{2}$ contains $K$; similarly, $A A_{2}$ will also pass through $K$. For this purpose, it suffices to prove that $$ \\Varangle\\left(C_{2} C, C_{2} A_{1}\\right)=\\Varangle\\left(B_{2} B, B_{2} A_{1}\\right) . $$ By the problem condition, $C B$ and $C A$ are the perpendicular bisectors of $T A_{1}$ and $T B_{1}$, respectively. Hence, $C$ is the circumcentre of the triangle $A_{1} T B_{1}$. Therefore, $$ \\Varangle\\left(C A_{1}, C B\\right)=\\Varangle(C B, C T)=\\Varangle\\left(B_{1} A_{1}, B_{1} T\\right)=\\Varangle\\left(B_{1} A_{1}, B_{1} B_{2}\\right) . $$ In circle $\\Omega$ we have $\\Varangle\\left(B_{1} A_{1}, B_{1} B_{2}\\right)=\\Varangle\\left(C_{2} A_{1}, C_{2} B_{2}\\right)$. Thus, $$ \\Varangle\\left(C A_{1}, C B\\right)=\\Varangle\\left(B_{1} A_{1}, B_{1} B_{2}\\right)=\\Varangle\\left(C_{2} A_{1}, C_{2} B_{2}\\right) . $$ Similarly, we get $$ \\Varangle\\left(B A_{1}, B C\\right)=\\Varangle\\left(C_{1} A_{1}, C_{1} C_{2}\\right)=\\Varangle\\left(B_{2} A_{1}, B_{2} C_{2}\\right) . $$ The two obtained relations yield that the triangles $A_{1} B C$ and $A_{1} B_{2} C_{2}$ are similar and equioriented, hence $$ \\frac{A_{1} B_{2}}{A_{1} B}=\\frac{A_{1} C_{2}}{A_{1} C} \\quad \\text { and } \\quad \\Varangle\\left(A_{1} B, A_{1} C\\right)=\\Varangle\\left(A_{1} B_{2}, A_{1} C_{2}\\right) $$ The second equality may be rewritten as $\\Varangle\\left(A_{1} B, A_{1} B_{2}\\right)=\\Varangle\\left(A_{1} C, A_{1} C_{2}\\right)$, so the triangles $A_{1} B B_{2}$ and $A_{1} C C_{2}$ are also similar and equioriented. This establishes (1). 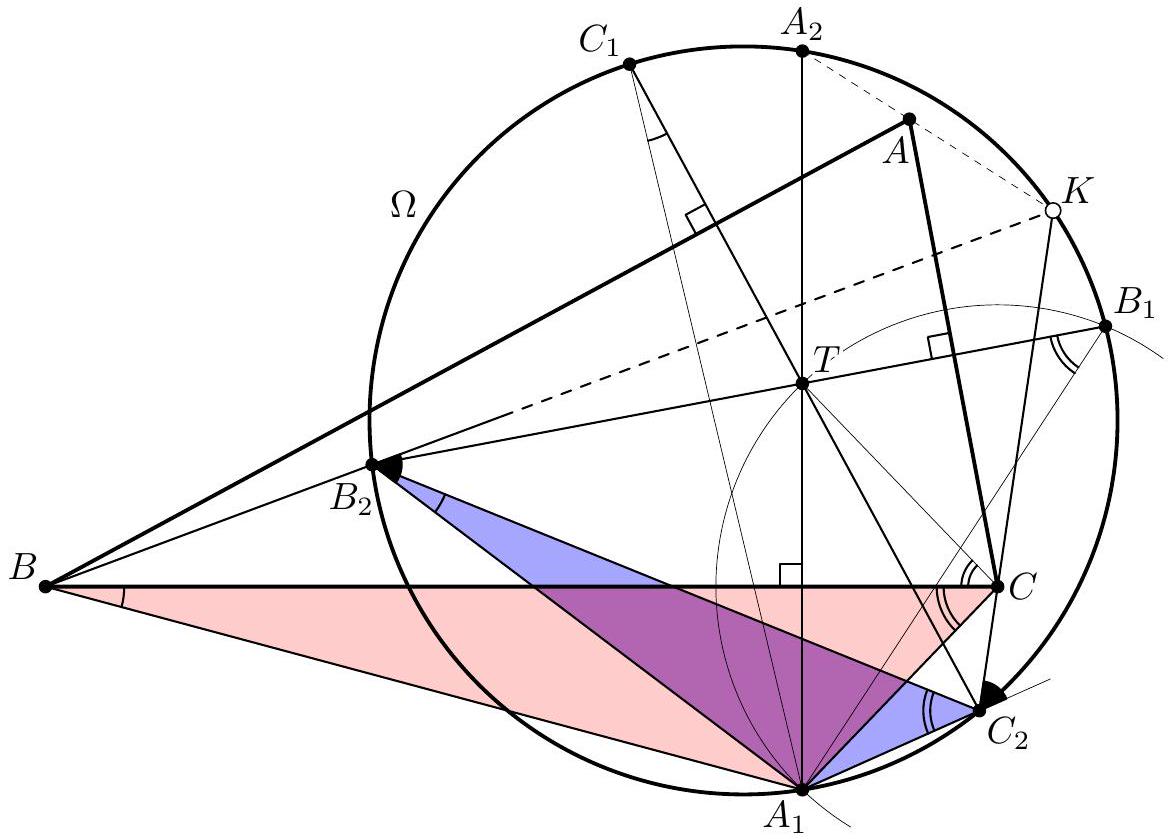 Comment 1. In fact, the triangle $A_{1} B C$ is an image of $A_{1} B_{2} C_{2}$ under a spiral similarity centred at $A_{1}$; in this case, the triangles $A B B_{2}$ and $A C C_{2}$ are also spirally similar with the same centre. Comment 2. After obtaining (2) and (3), one can finish the solution in different ways. For instance, introducing the point $X=B C \\cap B_{2} C_{2}$, one gets from these relations that the 4-tuples $\\left(A_{1}, B, B_{2}, X\\right)$ and $\\left(A_{1}, C, C_{2}, X\\right)$ are both cyclic. Therefore, $K$ is the Miquel point of the lines $B B_{2}$, $C C_{2}, B C$, and $B_{2} C_{2}$; this yields that the meeting point of $B B_{2}$ and $C C_{2}$ lies on $\\Omega$. Yet another way is to show that the points $A_{1}, B, C$, and $K$ are concyclic, as $$ \\Varangle\\left(K C, K A_{1}\\right)=\\Varangle\\left(B_{2} C_{2}, B_{2} A_{1}\\right)=\\Varangle\\left(B C, B A_{1}\\right) . $$ By symmetry, the second point $K^{\\prime}$ of intersection of $B B_{2}$ with $\\Omega$ is also concyclic to $A_{1}, B$, and $C$, hence $K^{\\prime}=K$.  Comment 3. The requirement that the common point of the lines $A A_{2}, B B_{2}$, and $C C_{2}$ should lie on $\\Omega$ may seem to make the problem easier, since it suggests some approaches. On the other hand, there are also different ways of showing that the lines $A A_{2}, B B_{2}$, and $C C_{2}$ are just concurrent. In particular, the problem conditions yield that the lines $A_{2} T, B_{2} T$, and $C_{2} T$ are perpendicular to the corresponding sides of the triangle $A B C$. One may show that the lines $A T, B T$, and $C T$ are also perpendicular to the corresponding sides of the triangle $A_{2} B_{2} C_{2}$, i.e., the triangles $A B C$ and $A_{2} B_{2} C_{2}$ are orthologic, and their orthology centres coincide. It is known that such triangles are also perspective, i.e. the lines $A A_{2}, B B_{2}$, and $C C_{2}$ are concurrent (in projective sense). To show this mutual orthology, one may again apply angle chasing, but there are also other methods. Let $A^{\\prime}, B^{\\prime}$, and $C^{\\prime}$ be the projections of $T$ onto the sides of the triangle $A B C$. Then $A_{2} T \\cdot T A^{\\prime}=$ $B_{2} T \\cdot T B^{\\prime}=C_{2} T \\cdot T C^{\\prime}$, since all three products equal (minus) half the power of $T$ with respect to $\\Omega$. This means that $A_{2}, B_{2}$, and $C_{2}$ are the poles of the sidelines of the triangle $A B C$ with respect to some circle centred at $T$ and having pure imaginary radius (in other words, the reflections of $A_{2}, B_{2}$, and $C_{2}$ in $T$ are the poles of those sidelines with respect to some regular circle centred at $T$ ). Hence, dually, the vertices of the triangle $A B C$ are also the poles of the sidelines of the triangle $A_{2} B_{2} C_{2}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with circumcircle $\\omega$ and incentre $I$. A line $\\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\\Theta$. Show that the circumcircle of the triangle $\\Theta$ is tangent to $\\omega$. (Denmark)", "solution": "Claim 1. The reflections $\\ell_{a}, \\ell_{b}$ and $\\ell_{c}$ of the line $\\ell$ in the lines $x, y$, and $z$, respectively, are concurrent at a point $T$ which belongs to $\\omega$.  Proof. Notice that $\\Varangle\\left(\\ell_{b}, \\ell_{c}\\right)=\\Varangle\\left(\\ell_{b}, \\ell\\right)+\\Varangle\\left(\\ell, \\ell_{c}\\right)=2 \\Varangle(y, \\ell)+2 \\Varangle(\\ell, z)=2 \\Varangle(y, z)$. But $y \\perp B I$ and $z \\perp C I$ implies $\\Varangle(y, z)=\\Varangle(B I, I C)$, so, since $2 \\Varangle(B I, I C)=\\Varangle(B A, A C)$, we obtain $$ \\Varangle\\left(\\ell_{b}, \\ell_{c}\\right)=\\Varangle(B A, A C) . $$ Since $A$ is the reflection of $D$ in $x$, $A$ belongs to $\\ell_{a}$; similarly, $B$ belongs to $\\ell_{b}$. Then (1) shows that the common point $T^{\\prime}$ of $\\ell_{a}$ and $\\ell_{b}$ lies on $\\omega$; similarly, the common point $T^{\\prime \\prime}$ of $\\ell_{c}$ and $\\ell_{b}$ lies on $\\omega$. If $B \\notin \\ell_{a}$ and $B \\notin \\ell_{c}$, then $T^{\\prime}$ and $T^{\\prime \\prime}$ are the second point of intersection of $\\ell_{b}$ and $\\omega$, hence they coincide. Otherwise, if, say, $B \\in \\ell_{c}$, then $\\ell_{c}=B C$, so $\\Varangle(B A, A C)=\\Varangle\\left(\\ell_{b}, \\ell_{c}\\right)=\\Varangle\\left(\\ell_{b}, B C\\right)$, which shows that $\\ell_{b}$ is tangent at $B$ to $\\omega$ and $T^{\\prime}=T^{\\prime \\prime}=B$. So $T^{\\prime}$ and $T^{\\prime \\prime}$ coincide in all the cases, and the conclusion of the claim follows. Now we prove that $X, X_{0}, T$ are collinear. Denote by $D_{b}$ and $D_{c}$ the reflections of the point $D$ in the lines $y$ and $z$, respectively. Then $D_{b}$ lies on $\\ell_{b}, D_{c}$ lies on $\\ell_{c}$, and $$ \\begin{aligned} \\Varangle\\left(D_{b} X, X D_{c}\\right) & =\\Varangle\\left(D_{b} X, D X\\right)+\\Varangle\\left(D X, X D_{c}\\right)=2 \\Varangle(y, D X)+2 \\Varangle(D X, z)=2 \\Varangle(y, z) \\\\ & =\\Varangle(B A, A C)=\\Varangle(B T, T C), \\end{aligned} $$ hence the quadrilateral $X D_{b} T D_{c}$ is cyclic. Notice also that since $X D_{b}=X D=X D_{c}$, the points $D, D_{b}, D_{c}$ lie on a circle with centre $X$. Using in this circle the diameter $D_{c} D_{c}^{\\prime}$ yields $\\Varangle\\left(D_{b} D_{c}, D_{c} X\\right)=90^{\\circ}+\\Varangle\\left(D_{b} D_{c}^{\\prime}, D_{c}^{\\prime} X\\right)=90^{\\circ}+\\Varangle\\left(D_{b} D, D D_{c}\\right)$. Therefore, $$ \\begin{gathered} \\Varangle\\left(\\ell_{b}, X T\\right)=\\Varangle\\left(D_{b} T, X T\\right)=\\Varangle\\left(D_{b} D_{c}, D_{c} X\\right)=90^{\\circ}+\\Varangle\\left(D_{b} D, D D_{c}\\right) \\\\ =90^{\\circ}+\\Varangle(B I, I C)=\\Varangle(B A, A I)=\\Varangle\\left(B A, A X_{0}\\right)=\\Varangle\\left(B T, T X_{0}\\right)=\\Varangle\\left(\\ell_{b}, X_{0} T\\right) \\end{gathered} $$ so the points $X, X_{0}, T$ are collinear. By a similar argument, $Y, Y_{0}, T$ and $Z, Z_{0}, T$ are collinear. As mentioned in the preamble, the statement of the problem follows. Comment 1. After proving Claim 1 one may proceed in another way. As it was shown, the reflections of $\\ell$ in the sidelines of $X Y Z$ are concurrent at $T$. Thus $\\ell$ is the Steiner line of $T$ with respect to $\\triangle X Y Z$ (that is the line containing the reflections $T_{a}, T_{b}, T_{c}$ of $T$ in the sidelines of $X Y Z$ ). The properties of the Steiner line imply that $T$ lies on $\\Omega$, and $\\ell$ passes through the orthocentre $H$ of the triangle $X Y Z$.  Let $H_{a}, H_{b}$, and $H_{c}$ be the reflections of the point $H$ in the lines $x, y$, and $z$, respectively. Then the triangle $H_{a} H_{b} H_{c}$ is inscribed in $\\Omega$ and homothetic to $A B C$ (by an easy angle chasing). Since $H_{a} \\in \\ell_{a}, H_{b} \\in \\ell_{b}$, and $H_{c} \\in \\ell_{c}$, the triangles $H_{a} H_{b} H_{c}$ and $A B C$ form a required pair of triangles $\\Delta$ and $\\delta$ mentioned in the preamble. Comment 2. The following observation shows how one may guess the description of the tangency point $T$ from Solution 1. Let us fix a direction and move the line $\\ell$ parallel to this direction with constant speed. Then the points $D, E$, and $F$ are moving with constant speeds along the lines $A I, B I$, and $C I$, respectively. In this case $x, y$, and $z$ are moving with constant speeds, defining a family of homothetic triangles $X Y Z$ with a common centre of homothety $T$. Notice that the triangle $X_{0} Y_{0} Z_{0}$ belongs to this family (for $\\ell$ passing through $I$ ). We may specify the location of $T$ considering the degenerate case when $x, y$, and $z$ are concurrent. In this degenerate case all the lines $x, y, z, \\ell, \\ell_{a}, \\ell_{b}, \\ell_{c}$ have a common point. Note that the lines $\\ell_{a}, \\ell_{b}, \\ell_{c}$ remain constant as $\\ell$ is moving (keeping its direction). Thus $T$ should be the common point of $\\ell_{a}, \\ell_{b}$, and $\\ell_{c}$, lying on $\\omega$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with circumcircle $\\omega$ and incentre $I$. A line $\\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\\Theta$. Show that the circumcircle of the triangle $\\Theta$ is tangent to $\\omega$. (Denmark)", "solution": "As mentioned in the preamble, it is sufficient to prove that the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\\omega$. Thus, it suffices to prove that $\\Varangle\\left(T X_{0}, T Y_{0}\\right)=$ $\\Varangle\\left(Z_{0} X_{0}, Z_{0} Y_{0}\\right)$, or, equivalently, $\\Varangle\\left(X X_{0}, Y Y_{0}\\right)=\\Varangle\\left(Z_{0} X_{0}, Z_{0} Y_{0}\\right)$. Recall that $Y Z$ and $Y_{0} Z_{0}$ are the perpendicular bisectors of $A D$ and $A I$, respectively. Then, the vector $\\vec{x}$ perpendicular to $Y Z$ and shifting the line $Y_{0} Z_{0}$ to $Y Z$ is equal to $\\frac{1}{2} \\overrightarrow{I D}$. Define the shifting vectors $\\vec{y}=\\frac{1}{2} \\overrightarrow{I E}, \\vec{z}=\\frac{1}{2} \\overrightarrow{I F}$ similarly. Consider now the triangle $U V W$ formed by the perpendiculars to $A I, B I$, and $C I$ through $D, E$, and $F$, respectively (see figure below). This is another triangle whose sides are parallel to the corresponding sides of $X Y Z$. Claim 2. $\\overrightarrow{I U}=2 \\overrightarrow{X_{0} X}, \\overrightarrow{I V}=2 \\overrightarrow{Y_{0} Y}, \\overrightarrow{I W}=2 \\overrightarrow{Z_{0} Z}$. Proof. We prove one of the relations, the other proofs being similar. To prove the equality of two vectors it suffices to project them onto two non-parallel axes and check that their projections are equal. The projection of $\\overrightarrow{X_{0} X}$ onto $I B$ equals $\\vec{y}$, while the projection of $\\overrightarrow{I U}$ onto $I B$ is $\\overrightarrow{I E}=2 \\vec{y}$. The projections onto the other axis $I C$ are $\\vec{z}$ and $\\overrightarrow{I F}=2 \\vec{z}$. Then $\\overrightarrow{I U}=2 \\overrightarrow{X_{0} X}$ follows. Notice that the line $\\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$; thus $U, V, W$, and $I$ are concyclic. It follows from Claim 2 that $\\Varangle\\left(X X_{0}, Y Y_{0}\\right)=\\Varangle(I U, I V)=$ $\\Varangle(W U, W V)=\\Varangle\\left(Z_{0} X_{0}, Z_{0} Y_{0}\\right)$, and we are done. ", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with circumcircle $\\omega$ and incentre $I$. A line $\\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\\Theta$. Show that the circumcircle of the triangle $\\Theta$ is tangent to $\\omega$. (Denmark)", "solution": "Let $I_{a}, I_{b}$, and $I_{c}$ be the excentres of triangle $A B C$ corresponding to $A, B$, and $C$, respectively. Also, let $u, v$, and $w$ be the lines through $D, E$, and $F$ which are perpendicular to $A I, B I$, and $C I$, respectively, and let $U V W$ be the triangle determined by these lines, where $u=V W, v=U W$ and $w=U V$ (see figure above). Notice that the line $u$ is the reflection of $I_{b} I_{c}$ in the line $x$, because $u, x$, and $I_{b} I_{c}$ are perpendicular to $A D$ and $x$ is the perpendicular bisector of $A D$. Likewise, $v$ and $I_{a} I_{c}$ are reflections of each other in $y$, while $w$ and $I_{a} I_{b}$ are reflections of each other in $z$. It follows that $X, Y$, and $Z$ are the midpoints of $U I_{a}, V I_{b}$ and $W I_{c}$, respectively, and that the triangles $U V W$, $X Y Z$ and $I_{a} I_{b} I_{c}$ are either translates of each other or homothetic with a common homothety centre. Construct the points $T$ and $S$ such that the quadrilaterals $U V I W, X Y T Z$ and $I_{a} I_{b} S I_{c}$ are homothetic. Then $T$ is the midpoint of $I S$. Moreover, note that $\\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$, hence $I$ belongs to the circumcircle of the triangle $U V W$, therefore $T$ belongs to $\\Omega$. Consider now the homothety or translation $h_{1}$ that maps $X Y Z T$ to $I_{a} I_{b} I_{c} S$ and the homothety $h_{2}$ with centre $I$ and factor $\\frac{1}{2}$. Furthermore, let $h=h_{2} \\circ h_{1}$. The transform $h$ can be a homothety or a translation, and $$ h(T)=h_{2}\\left(h_{1}(T)\\right)=h_{2}(S)=T $$ hence $T$ is a fixed point of $h$. So, $h$ is a homothety with centre $T$. Note that $h_{2}$ maps the excentres $I_{a}, I_{b}, I_{c}$ to $X_{0}, Y_{0}, Z_{0}$ defined in the preamble. Thus the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\\Omega$, and this completes the proof.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G6", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "A convex quadrilateral $A B C D$ satisfies $A B \\cdot C D=B C \\cdot D A$. A point $X$ is chosen inside the quadrilateral so that $\\angle X A B=\\angle X C D$ and $\\angle X B C=\\angle X D A$. Prove that $\\angle A X B+$ $\\angle C X D=180^{\\circ}$. (Poland)", "solution": "Let $B^{\\prime}$ be the reflection of $B$ in the internal angle bisector of $\\angle A X C$, so that $\\angle A X B^{\\prime}=\\angle C X B$ and $\\angle C X B^{\\prime}=\\angle A X B$. If $X, D$, and $B^{\\prime}$ are collinear, then we are done. Now assume the contrary. On the ray $X B^{\\prime}$ take a point $E$ such that $X E \\cdot X B=X A \\cdot X C$, so that $\\triangle A X E \\sim$ $\\triangle B X C$ and $\\triangle C X E \\sim \\triangle B X A$. We have $\\angle X C E+\\angle X C D=\\angle X B A+\\angle X A B<180^{\\circ}$ and $\\angle X A E+\\angle X A D=\\angle X D A+\\angle X A D<180^{\\circ}$, which proves that $X$ lies inside the angles $\\angle E C D$ and $\\angle E A D$ of the quadrilateral $E A D C$. Moreover, $X$ lies in the interior of exactly one of the two triangles $E A D, E C D$ (and in the exterior of the other). 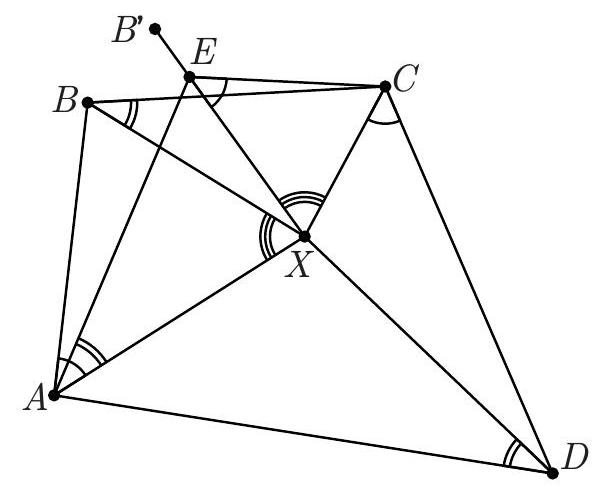 The similarities mentioned above imply $X A \\cdot B C=X B \\cdot A E$ and $X B \\cdot C E=X C \\cdot A B$. Multiplying these equalities with the given equality $A B \\cdot C D=B C \\cdot D A$, we obtain $X A \\cdot C D$. $C E=X C \\cdot A D \\cdot A E$, or, equivalently, $$ \\frac{X A \\cdot D E}{A D \\cdot A E}=\\frac{X C \\cdot D E}{C D \\cdot C E} $$ Lemma. Let $P Q R$ be a triangle, and let $X$ be a point in the interior of the angle $Q P R$ such that $\\angle Q P X=\\angle P R X$. Then $\\frac{P X \\cdot Q R}{P Q \\cdot P R}<1$ if and only if $X$ lies in the interior of the triangle $P Q R$. Proof. The locus of points $X$ with $\\angle Q P X=\\angle P R X$ lying inside the angle $Q P R$ is an arc $\\alpha$ of the circle $\\gamma$ through $R$ tangent to $P Q$ at $P$. Let $\\gamma$ intersect the line $Q R$ again at $Y$ (if $\\gamma$ is tangent to $Q R$, then set $Y=R)$. The similarity $\\triangle Q P Y \\sim \\triangle Q R P$ yields $P Y=\\frac{P Q \\cdot P R}{Q R}$. Now it suffices to show that $P X<P Y$ if and only if $X$ lies in the interior of the triangle $P Q R$. Let $m$ be a line through $Y$ parallel to $P Q$. Notice that the points $Z$ of $\\gamma$ satisfying $P Z<P Y$ are exactly those between the lines $m$ and $P Q$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G6", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "A convex quadrilateral $A B C D$ satisfies $A B \\cdot C D=B C \\cdot D A$. A point $X$ is chosen inside the quadrilateral so that $\\angle X A B=\\angle X C D$ and $\\angle X B C=\\angle X D A$. Prove that $\\angle A X B+$ $\\angle C X D=180^{\\circ}$. (Poland)", "solution": "The solution consists of two parts. In Part 1 we show that it suffices to prove that $$ \\frac{X B}{X D}=\\frac{A B}{C D} $$ and $$ \\frac{X A}{X C}=\\frac{D A}{B C} $$ In Part 2 we establish these equalities. Part 1. Using the sine law and applying (1) we obtain $$ \\frac{\\sin \\angle A X B}{\\sin \\angle X A B}=\\frac{A B}{X B}=\\frac{C D}{X D}=\\frac{\\sin \\angle C X D}{\\sin \\angle X C D} $$ so $\\sin \\angle A X B=\\sin \\angle C X D$ by the problem conditions. Similarly, (2) yields $\\sin \\angle D X A=$ $\\sin \\angle B X C$. If at least one of the pairs $(\\angle A X B, \\angle C X D)$ and $(\\angle B X C, \\angle D X A)$ consists of supplementary angles, then we are done. Otherwise, $\\angle A X B=\\angle C X D$ and $\\angle D X A=\\angle B X C$. In this case $X=A C \\cap B D$, and the problem conditions yield that $A B C D$ is a parallelogram and hence a rhombus. In this last case the claim also holds. Part 2. To prove the desired equality (1), invert $A B C D$ at centre $X$ with unit radius; the images of points are denoted by primes. We have $$ \\angle A^{\\prime} B^{\\prime} C^{\\prime}=\\angle X B^{\\prime} A^{\\prime}+\\angle X B^{\\prime} C^{\\prime}=\\angle X A B+\\angle X C B=\\angle X C D+\\angle X C B=\\angle B C D . $$ Similarly, the corresponding angles of quadrilaterals $A B C D$ and $D^{\\prime} A^{\\prime} B^{\\prime} C^{\\prime}$ are equal. Moreover, we have $$ A^{\\prime} B^{\\prime} \\cdot C^{\\prime} D^{\\prime}=\\frac{A B}{X A \\cdot X B} \\cdot \\frac{C D}{X C \\cdot X D}=\\frac{B C}{X B \\cdot X C} \\cdot \\frac{D A}{X D \\cdot D A}=B^{\\prime} C^{\\prime} \\cdot D^{\\prime} A^{\\prime} $$ 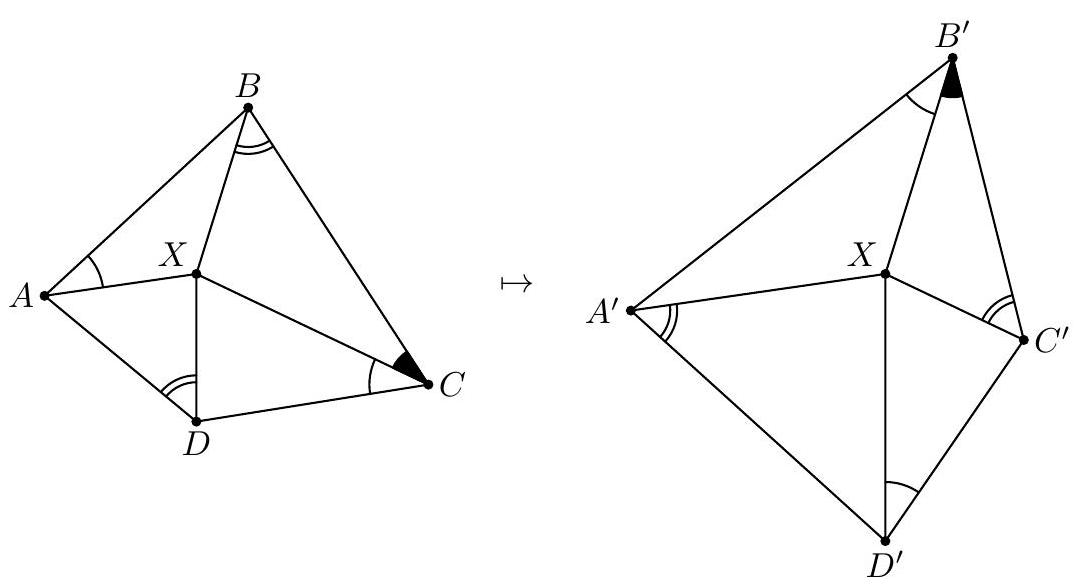 Now we need the following Lemma. Lemma. Assume that the corresponding angles of convex quadrilaterals $X Y Z T$ and $X^{\\prime} Y^{\\prime} Z^{\\prime} T^{\\prime}$ are equal, and that $X Y \\cdot Z T=Y Z \\cdot T X$ and $X^{\\prime} Y^{\\prime} \\cdot Z^{\\prime} T^{\\prime}=Y^{\\prime} Z^{\\prime} \\cdot T^{\\prime} X^{\\prime}$. Then the two quadrilaterals are similar. Proof. Take the quadrilateral $X Y Z_{1} T_{1}$ similar to $X^{\\prime} Y^{\\prime} Z^{\\prime} T^{\\prime}$ and sharing the side $X Y$ with $X Y Z T$, such that $Z_{1}$ and $T_{1}$ lie on the rays $Y Z$ and $X T$, respectively, and $Z_{1} T_{1} \\| Z T$. We need to prove that $Z_{1}=Z$ and $T_{1}=T$. Assume the contrary. Without loss of generality, $T X>X T_{1}$. Let segments $X Z$ and $Z_{1} T_{1}$ intersect at $U$. We have $$ \\frac{T_{1} X}{T_{1} Z_{1}}<\\frac{T_{1} X}{T_{1} U}=\\frac{T X}{Z T}=\\frac{X Y}{Y Z}<\\frac{X Y}{Y Z_{1}} $$ thus $T_{1} X \\cdot Y Z_{1}<T_{1} Z_{1} \\cdot X Y$. A contradiction. 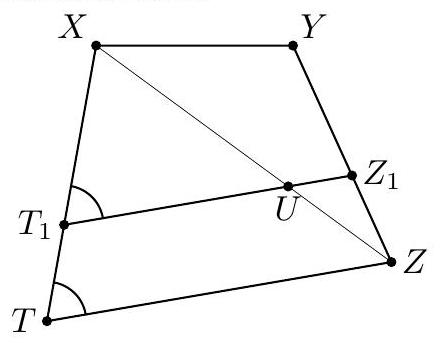 It follows from the Lemma that the quadrilaterals $A B C D$ and $D^{\\prime} A^{\\prime} B^{\\prime} C^{\\prime}$ are similar, hence $$ \\frac{B C}{A B}=\\frac{A^{\\prime} B^{\\prime}}{D^{\\prime} A^{\\prime}}=\\frac{A B}{X A \\cdot X B} \\cdot \\frac{X D \\cdot X A}{D A}=\\frac{A B}{A D} \\cdot \\frac{X D}{X B} $$ and therefore $$ \\frac{X B}{X D}=\\frac{A B^{2}}{B C \\cdot A D}=\\frac{A B^{2}}{A B \\cdot C D}=\\frac{A B}{C D} $$ We obtain (1), as desired; (2) is proved similarly. Comment. Part 1 is an easy one, while part 2 seems to be crucial. On the other hand, after the proof of the similarity $D^{\\prime} A^{\\prime} B^{\\prime} C^{\\prime} \\sim A B C D$ one may finish the solution in different ways, e.g., as follows. The similarity taking $D^{\\prime} A^{\\prime} B^{\\prime} C^{\\prime}$ to $A B C D$ maps $X$ to the point $X^{\\prime}$ isogonally conjugate of $X$ with respect to $A B C D$ (i.e. to the point $X^{\\prime}$ inside $A B C D$ such that $\\angle B A X=\\angle D A X^{\\prime}$, $\\left.\\angle C B X=\\angle A B X^{\\prime}, \\angle D C X=\\angle B C X^{\\prime}, \\angle A D X=\\angle C D X^{\\prime}\\right)$. It is known that the required equality $\\angle A X B+\\angle C X D=180^{\\circ}$ is one of known conditions on a point $X$ inside $A B C D$ equivalent to the existence of its isogonal conjugate. This page is intentionally left blank", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G7", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $O$ be the circumcentre, and $\\Omega$ be the circumcircle of an acute-angled triangle $A B C$. Let $P$ be an arbitrary point on $\\Omega$, distinct from $A, B, C$, and their antipodes in $\\Omega$. Denote the circumcentres of the triangles $A O P, B O P$, and $C O P$ by $O_{A}, O_{B}$, and $O_{C}$, respectively. The lines $\\ell_{A}, \\ell_{B}$, and $\\ell_{C}$ perpendicular to $B C, C A$, and $A B$ pass through $O_{A}, O_{B}$, and $O_{C}$, respectively. Prove that the circumcircle of the triangle formed by $\\ell_{A}, \\ell_{B}$, and $\\ell_{C}$ is tangent to the line $O P$. (Russia)", "solution": "As usual, we denote the directed angle between the lines $a$ and $b$ by $\\Varangle(a, b)$. We frequently use the fact that $a_{1} \\perp a_{2}$ and $b_{1} \\perp b_{2}$ yield $\\Varangle\\left(a_{1}, b_{1}\\right)=\\Varangle\\left(a_{2}, b_{2}\\right)$. Let the lines $\\ell_{B}$ and $\\ell_{C}$ meet at $L_{A}$; define the points $L_{B}$ and $L_{C}$ similarly. Note that the sidelines of the triangle $L_{A} L_{B} L_{C}$ are perpendicular to the corresponding sidelines of $A B C$. Points $O_{A}, O_{B}, O_{C}$ are located on the corresponding sidelines of $L_{A} L_{B} L_{C}$; moreover, $O_{A}, O_{B}$, $O_{C}$ all lie on the perpendicular bisector of $O P$. 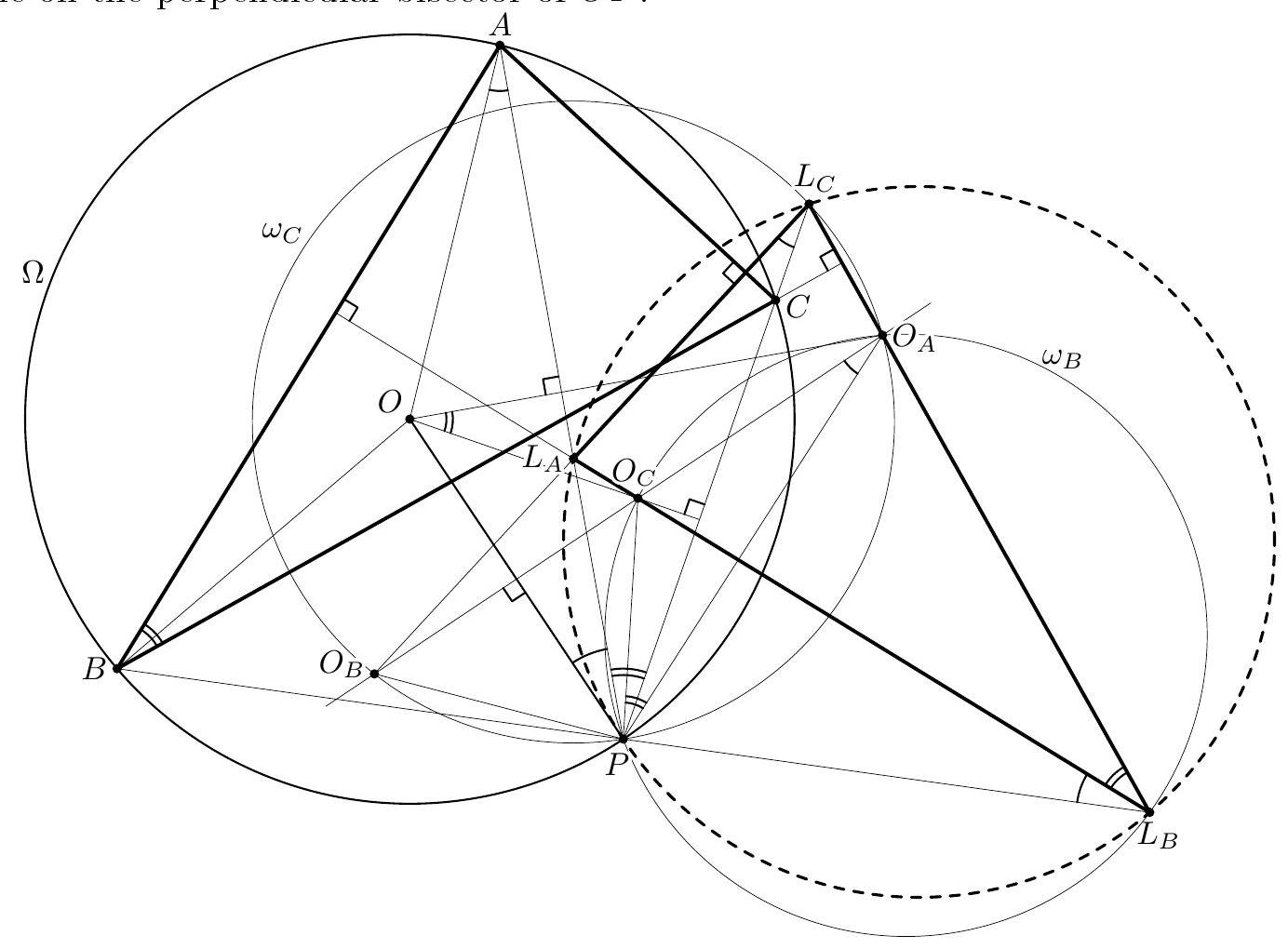 Claim 1. The points $L_{B}, P, O_{A}$, and $O_{C}$ are concyclic. Proof. Since $O$ is symmetric to $P$ in $O_{A} O_{C}$, we have $$ \\Varangle\\left(O_{A} P, O_{C} P\\right)=\\Varangle\\left(O_{C} O, O_{A} O\\right)=\\Varangle(C P, A P)=\\Varangle(C B, A B)=\\Varangle\\left(O_{A} L_{B}, O_{C} L_{B}\\right) . $$ Denote the circle through $L_{B}, P, O_{A}$, and $O_{C}$ by $\\omega_{B}$. Define the circles $\\omega_{A}$ and $\\omega_{C}$ similarly. Claim 2. The circumcircle of the triangle $L_{A} L_{B} L_{C}$ passes through $P$. Proof. From cyclic quadruples of points in the circles $\\omega_{B}$ and $\\omega_{C}$, we have $$ \\begin{aligned} \\Varangle\\left(L_{C} L_{A}, L_{C} P\\right) & =\\Varangle\\left(L_{C} O_{B}, L_{C} P\\right)=\\Varangle\\left(O_{A} O_{B}, O_{A} P\\right) \\\\ & =\\Varangle\\left(O_{A} O_{C}, O_{A} P\\right)=\\Varangle\\left(L_{B} O_{C}, L_{B} P\\right)=\\Varangle\\left(L_{B} L_{A}, L_{B} P\\right) . \\end{aligned} $$ Claim 3. The points $P, L_{C}$, and $C$ are collinear. Proof. We have $\\Varangle\\left(P L_{C}, L_{C} L_{A}\\right)=\\Varangle\\left(P L_{C}, L_{C} O_{B}\\right)=\\Varangle\\left(P O_{A}, O_{A} O_{B}\\right)$. Further, since $O_{A}$ is the centre of the circle $A O P, \\Varangle\\left(P O_{A}, O_{A} O_{B}\\right)=\\Varangle(P A, A O)$. As $O$ is the circumcentre of the triangle $P C A, \\Varangle(P A, A O)=\\pi / 2-\\Varangle(C A, C P)=\\Varangle\\left(C P, L_{C} L_{A}\\right)$. We obtain $\\Varangle\\left(P L_{C}, L_{C} L_{A}\\right)=$ $\\Varangle\\left(C P, L_{C} L_{A}\\right)$, which shows that $P \\in C L_{C}$. Similarly, the points $P, L_{A}, A$ are collinear, and the points $P, L_{B}, B$ are also collinear. Finally, the computation above also shows that $$ \\Varangle\\left(O P, P L_{A}\\right)=\\Varangle(P A, A O)=\\Varangle\\left(P L_{C}, L_{C} L_{A}\\right) $$ which means that $O P$ is tangent to the circle $P L_{A} L_{B} L_{C}$. Comment 1. The proof of Claim 2 may be replaced by the following remark: since $P$ belongs to the circles $\\omega_{A}$ and $\\omega_{C}, P$ is the Miquel point of the four lines $\\ell_{A}, \\ell_{B}, \\ell_{C}$, and $O_{A} O_{B} O_{C}$. Comment 2. Claims 2 and 3 can be proved in several different ways and, in particular, in the reverse order. Claim 3 implies that the triangles $A B C$ and $L_{A} L_{B} L_{C}$ are perspective with perspector $P$. Claim 2 can be derived from this observation using spiral similarity. Consider the centre $Q$ of the spiral similarity that maps $A B C$ to $L_{A} L_{B} L_{C}$. From known spiral similarity properties, the points $L_{A}, L_{B}, P, Q$ are concyclic, and so are $L_{A}, L_{C}, P, Q$. Comment 3. The final conclusion can also be proved it terms of spiral similarity: the spiral similarity with centre $Q$ located on the circle $A B C$ maps the circle $A B C$ to the circle $P L_{A} L_{B} L_{C}$. Thus these circles are orthogonal. Comment 4. Notice that the homothety with centre $O$ and ratio 2 takes $O_{A}$ to $A^{\\prime}$ that is the common point of tangents to $\\Omega$ at $A$ and $P$. Similarly, let this homothety take $O_{B}$ to $B^{\\prime}$ and $O_{C}$ to $C^{\\prime}$. Let the tangents to $\\Omega$ at $B$ and $C$ meet at $A^{\\prime \\prime}$, and define the points $B^{\\prime \\prime}$ and $C^{\\prime \\prime}$ similarly. Now, replacing labels $O$ with $I, \\Omega$ with $\\omega$, and swapping labels $A \\leftrightarrow A^{\\prime \\prime}, B \\leftrightarrow B^{\\prime \\prime}, C \\leftrightarrow C^{\\prime \\prime}$ we obtain the following Reformulation. Let $\\omega$ be the incircle, and let $I$ be the incentre of a triangle $A B C$. Let $P$ be a point of $\\omega$ (other than the points of contact of $\\omega$ with the sides of $A B C$ ). The tangent to $\\omega$ at $P$ meets the lines $A B, B C$, and $C A$ at $A^{\\prime}, B^{\\prime}$, and $C^{\\prime}$, respectively. Line $\\ell_{A}$ parallel to the internal angle bisector of $\\angle B A C$ passes through $A^{\\prime}$; define lines $\\ell_{B}$ and $\\ell_{C}$ similarly. Prove that the line $I P$ is tangent to the circumcircle of the triangle formed by $\\ell_{A}, \\ell_{B}$, and $\\ell_{C}$. Though this formulation is equivalent to the original one, it seems more challenging, since the point of contact is now \"hidden\".", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N1", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Determine all pairs $(n, k)$ of distinct positive integers such that there exists a positive integer $s$ for which the numbers of divisors of $s n$ and of $s k$ are equal. (Ukraine)", "solution": "As usual, the number of divisors of a positive integer $n$ is denoted by $d(n)$. If $n=\\prod_{i} p_{i}^{\\alpha_{i}}$ is the prime factorisation of $n$, then $d(n)=\\prod_{i}\\left(\\alpha_{i}+1\\right)$. We start by showing that one cannot find any suitable number $s$ if $k \\mid n$ or $n \\mid k$ (and $k \\neq n$ ). Suppose that $n \\mid k$, and choose any positive integer $s$. Then the set of divisors of $s n$ is a proper subset of that of $s k$, hence $d(s n)<d(s k)$. Therefore, the pair $(n, k)$ does not satisfy the problem requirements. The case $k \\mid n$ is similar. Now assume that $n \\nmid k$ and $k \\nmid n$. Let $p_{1}, \\ldots, p_{t}$ be all primes dividing $n k$, and consider the prime factorisations $$ n=\\prod_{i=1}^{t} p_{i}^{\\alpha_{i}} \\quad \\text { and } \\quad k=\\prod_{i=1}^{t} p_{i}^{\\beta_{i}} $$ It is reasonable to search for the number $s$ having the form $$ s=\\prod_{i=1}^{t} p_{i}^{\\gamma_{i}} $$ The (nonnegative integer) exponents $\\gamma_{i}$ should be chosen so as to satisfy $$ \\frac{d(s n)}{d(s k)}=\\prod_{i=1}^{t} \\frac{\\alpha_{i}+\\gamma_{i}+1}{\\beta_{i}+\\gamma_{i}+1}=1 $$ First of all, if $\\alpha_{i}=\\beta_{i}$ for some $i$, then, regardless of the value of $\\gamma_{i}$, the corresponding factor in (1) equals 1 and does not affect the product. So we may assume that there is no such index $i$. For the other factors in (1), the following lemma is useful. Lemma. Let $\\alpha>\\beta$ be nonnegative integers. Then, for every integer $M \\geqslant \\beta+1$, there exists a nonnegative integer $\\gamma$ such that $$ \\frac{\\alpha+\\gamma+1}{\\beta+\\gamma+1}=1+\\frac{1}{M}=\\frac{M+1}{M} . $$ Proof. $$ \\frac{\\alpha+\\gamma+1}{\\beta+\\gamma+1}=1+\\frac{1}{M} \\Longleftrightarrow \\frac{\\alpha-\\beta}{\\beta+\\gamma+1}=\\frac{1}{M} \\Longleftrightarrow \\gamma=M(\\alpha-\\beta)-(\\beta+1) \\geqslant 0 . $$ Now we can finish the solution. Without loss of generality, there exists an index $u$ such that $\\alpha_{i}>\\beta_{i}$ for $i=1,2, \\ldots, u$, and $\\alpha_{i}<\\beta_{i}$ for $i=u+1, \\ldots, t$. The conditions $n \\nmid k$ and $k \\nmid n$ mean that $1 \\leqslant u \\leqslant t-1$. Choose an integer $X$ greater than all the $\\alpha_{i}$ and $\\beta_{i}$. By the lemma, we can define the numbers $\\gamma_{i}$ so as to satisfy $$ \\begin{array}{ll} \\frac{\\alpha_{i}+\\gamma_{i}+1}{\\beta_{i}+\\gamma_{i}+1}=\\frac{u X+i}{u X+i-1} & \\text { for } i=1,2, \\ldots, u, \\text { and } \\\\ \\frac{\\beta_{u+i}+\\gamma_{u+i}+1}{\\alpha_{u+i}+\\gamma_{u+i}+1}=\\frac{(t-u) X+i}{(t-u) X+i-1} & \\text { for } i=1,2, \\ldots, t-u . \\end{array} $$ Then we will have $$ \\frac{d(s n)}{d(s k)}=\\prod_{i=1}^{u} \\frac{u X+i}{u X+i-1} \\cdot \\prod_{i=1}^{t-u} \\frac{(t-u) X+i-1}{(t-u) X+i}=\\frac{u(X+1)}{u X} \\cdot \\frac{(t-u) X}{(t-u)(X+1)}=1, $$ as required. Comment. The lemma can be used in various ways, in order to provide a suitable value of $s$. In particular, one may apply induction on the number $t$ of prime factors, using identities like $$ \\frac{n}{n-1}=\\frac{n^{2}}{n^{2}-1} \\cdot \\frac{n+1}{n} $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N2", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $n>1$ be a positive integer. Each cell of an $n \\times n$ table contains an integer. Suppose that the following conditions are satisfied: (i) Each number in the table is congruent to 1 modulo $n$; (ii) The sum of numbers in any row, as well as the sum of numbers in any column, is congruent to $n$ modulo $n^{2}$. Let $R_{i}$ be the product of the numbers in the $i^{\\text {th }}$ row, and $C_{j}$ be the product of the numbers in the $j^{\\text {th }}$ column. Prove that the sums $R_{1}+\\cdots+R_{n}$ and $C_{1}+\\cdots+C_{n}$ are congruent modulo $n^{4}$. (Indonesia)", "solution": "Let $A_{i, j}$ be the entry in the $i^{\\text {th }}$ row and the $j^{\\text {th }}$ column; let $P$ be the product of all $n^{2}$ entries. For convenience, denote $a_{i, j}=A_{i, j}-1$ and $r_{i}=R_{i}-1$. We show that $$ \\sum_{i=1}^{n} R_{i} \\equiv(n-1)+P \\quad\\left(\\bmod n^{4}\\right) $$ Due to symmetry of the problem conditions, the sum of all the $C_{j}$ is also congruent to $(n-1)+P$ modulo $n^{4}$, whence the conclusion. By condition $(i)$, the number $n$ divides $a_{i, j}$ for all $i$ and $j$. So, every product of at least two of the $a_{i, j}$ is divisible by $n^{2}$, hence $R_{i}=\\prod_{j=1}^{n}\\left(1+a_{i, j}\\right)=1+\\sum_{j=1}^{n} a_{i, j}+\\sum_{1 \\leqslant j_{1}<j_{2} \\leqslant n} a_{i, j_{1}} a_{i, j_{2}}+\\cdots \\equiv 1+\\sum_{j=1}^{n} a_{i, j} \\equiv 1-n+\\sum_{j=1}^{n} A_{i, j} \\quad\\left(\\bmod n^{2}\\right)$ for every index $i$. Using condition (ii), we obtain $R_{i} \\equiv 1\\left(\\bmod n^{2}\\right)$, and so $n^{2} \\mid r_{i}$. Therefore, every product of at least two of the $r_{i}$ is divisible by $n^{4}$. Repeating the same argument, we obtain $$ P=\\prod_{i=1}^{n} R_{i}=\\prod_{i=1}^{n}\\left(1+r_{i}\\right) \\equiv 1+\\sum_{i=1}^{n} r_{i} \\quad\\left(\\bmod n^{4}\\right) $$ whence $$ \\sum_{i=1}^{n} R_{i}=n+\\sum_{i=1}^{n} r_{i} \\equiv n+(P-1) \\quad\\left(\\bmod n^{4}\\right) $$ as desired. Comment. The original version of the problem statement contained also the condition (iii) The product of all the numbers in the table is congruent to 1 modulo $n^{4}$. This condition appears to be superfluous, so it was omitted.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N2", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $n>1$ be a positive integer. Each cell of an $n \\times n$ table contains an integer. Suppose that the following conditions are satisfied: (i) Each number in the table is congruent to 1 modulo $n$; (ii) The sum of numbers in any row, as well as the sum of numbers in any column, is congruent to $n$ modulo $n^{2}$. Let $R_{i}$ be the product of the numbers in the $i^{\\text {th }}$ row, and $C_{j}$ be the product of the numbers in the $j^{\\text {th }}$ column. Prove that the sums $R_{1}+\\cdots+R_{n}$ and $C_{1}+\\cdots+C_{n}$ are congruent modulo $n^{4}$. (Indonesia)", "solution": "We present a more straightforward (though lengthier) way to establish (1). We also use the notation of $a_{i, j}$. By condition (i), all the $a_{i, j}$ are divisible by $n$. Therefore, we have $$ \\begin{aligned} P=\\prod_{i=1}^{n} \\prod_{j=1}^{n}\\left(1+a_{i, j}\\right) \\equiv 1+\\sum_{(i, j)} a_{i, j} & +\\sum_{\\left(i_{1}, j_{1}\\right),\\left(i_{2}, j_{2}\\right)} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}} \\\\ & +\\sum_{\\left(i_{1}, j_{1}\\right),\\left(i_{2}, j_{2}\\right),\\left(i_{3}, j_{3}\\right)} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}} a_{i_{3}, j_{3}}\\left(\\bmod n^{4}\\right), \\end{aligned} $$ where the last two sums are taken over all unordered pairs/triples of pairwise different pairs $(i, j)$; such conventions are applied throughout the solution. Similarly, $$ \\sum_{i=1}^{n} R_{i}=\\sum_{i=1}^{n} \\prod_{j=1}^{n}\\left(1+a_{i, j}\\right) \\equiv n+\\sum_{i} \\sum_{j} a_{i, j}+\\sum_{i} \\sum_{j_{1}, j_{2}} a_{i, j_{1}} a_{i, j_{2}}+\\sum_{i} \\sum_{j_{1}, j_{2}, j_{3}} a_{i, j_{1}} a_{i, j_{2}} a_{i, j_{3}} \\quad\\left(\\bmod n^{4}\\right) $$ Therefore, $$ \\begin{aligned} P+(n-1)-\\sum_{i} R_{i} \\equiv \\sum_{\\substack{\\left(i_{1}, j_{1}\\right),\\left(i_{2}, j_{2}\\right) \\\\ i_{1} \\neq i_{2}}} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}} & +\\sum_{\\substack{\\left(i_{1}, j_{1}\\right),\\left(i_{2}, j_{2}\\right),\\left(i_{3}, j_{3}\\right) \\\\ i_{1} \\neq i_{2} \\neq i_{3} \\neq i_{1}}} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}} a_{i_{3}, j_{3}} \\\\ & +\\sum_{\\substack{\\left(i_{1}, j_{1}\\right),\\left(i_{2}, j_{2}\\right),\\left(i_{3}, j_{3}\\right) \\\\ i_{1} \\neq i_{2}=i_{3}}} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}} a_{i_{3}, j_{3}}\\left(\\bmod n^{4}\\right) . \\end{aligned} $$ We show that in fact each of the three sums appearing in the right-hand part of this congruence is divisible by $n^{4}$; this yields (1). Denote those three sums by $\\Sigma_{1}, \\Sigma_{2}$, and $\\Sigma_{3}$ in order of appearance. Recall that by condition (ii) we have $$ \\sum_{j} a_{i, j} \\equiv 0 \\quad\\left(\\bmod n^{2}\\right) \\quad \\text { for all indices } i $$ For every two indices $i_{1}<i_{2}$ we have $$ \\sum_{j_{1}} \\sum_{j_{2}} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}}=\\left(\\sum_{j_{1}} a_{i_{1}, j_{1}}\\right) \\cdot\\left(\\sum_{j_{2}} a_{i_{2}, j_{2}}\\right) \\equiv 0 \\quad\\left(\\bmod n^{4}\\right) $$ since each of the two factors is divisible by $n^{2}$. Summing over all pairs $\\left(i_{1}, i_{2}\\right)$ we obtain $n^{4} \\mid \\Sigma_{1}$. Similarly, for every three indices $i_{1}<i_{2}<i_{3}$ we have $$ \\sum_{j_{1}} \\sum_{j_{2}} \\sum_{j_{3}} a_{i_{1}, j_{1}} a_{i_{2}, j_{2}} a_{i_{3}, j_{3}}=\\left(\\sum_{j_{1}} a_{i_{1}, j_{1}}\\right) \\cdot\\left(\\sum_{j_{2}} a_{i_{2}, j_{2}}\\right) \\cdot\\left(\\sum_{j_{3}} a_{i_{3}, j_{3}}\\right) $$ which is divisible even by $n^{6}$. Hence $n^{4} \\mid \\Sigma_{2}$. Finally, for every indices $i_{1} \\neq i_{2}=i_{3}$ and $j_{2}<j_{3}$ we have $$ a_{i_{2}, j_{2}} \\cdot a_{i_{2}, j_{3}} \\cdot \\sum_{j_{1}} a_{i_{1}, j_{1}} \\equiv 0 \\quad\\left(\\bmod n^{4}\\right) $$ since the three factors are divisible by $n, n$, and $n^{2}$, respectively. Summing over all 4 -tuples of indices $\\left(i_{1}, i_{2}, j_{2}, j_{3}\\right)$ we get $n^{4} \\mid \\Sigma_{3}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N3", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Define the sequence $a_{0}, a_{1}, a_{2}, \\ldots$ by $a_{n}=2^{n}+2^{\\lfloor n / 2\\rfloor}$. Prove that there are infinitely many terms of the sequence which can be expressed as a sum of (two or more) distinct terms of the sequence, as well as infinitely many of those which cannot be expressed in such a way. (Serbia)", "solution": "Call a nonnegative integer representable if it equals the sum of several (possibly 0 or 1) distinct terms of the sequence. We say that two nonnegative integers $b$ and $c$ are equivalent (written as $b \\sim c$ ) if they are either both representable or both non-representable. One can easily compute $$ S_{n-1}:=a_{0}+\\cdots+a_{n-1}=2^{n}+2^{\\lceil n / 2\\rceil}+2^{\\lfloor n / 2\\rfloor}-3 . $$ Indeed, we have $S_{n}-S_{n-1}=2^{n}+2^{\\lfloor n / 2\\rfloor}=a_{n}$ so we can use the induction. In particular, $S_{2 k-1}=2^{2 k}+2^{k+1}-3$. Note that, if $n \\geqslant 3$, then $2^{[n / 2]} \\geqslant 2^{2}>3$, so $$ S_{n-1}=2^{n}+2^{\\lceil n / 2\\rceil}+2^{\\lfloor n / 2\\rfloor}-3>2^{n}+2^{\\lfloor n / 2\\rfloor}=a_{n} . $$ Also notice that $S_{n-1}-a_{n}=2^{[n / 2]}-3<a_{n}$. The main tool of the solution is the following claim. Claim 1. Assume that $b$ is a positive integer such that $S_{n-1}-a_{n}<b<a_{n}$ for some $n \\geqslant 3$. Then $b \\sim S_{n-1}-b$. Proof. As seen above, we have $S_{n-1}>a_{n}$. Denote $c=S_{n-1}-b$; then $S_{n-1}-a_{n}<c<a_{n}$, so the roles of $b$ and $c$ are symmetrical. Assume that $b$ is representable. The representation cannot contain $a_{i}$ with $i \\geqslant n$, since $b<a_{n}$. So $b$ is the sum of some subset of $\\left\\{a_{0}, a_{1}, \\ldots, a_{n-1}\\right\\}$; then $c$ is the sum of the complement. The converse is obtained by swapping $b$ and $c$. We also need the following version of this claim. Claim 2. For any $n \\geqslant 3$, the number $a_{n}$ can be represented as a sum of two or more distinct terms of the sequence if and only if $S_{n-1}-a_{n}=2^{[n / 2]}-3$ is representable. Proof. Denote $c=S_{n-1}-a_{n}<a_{n}$. If $a_{n}$ satisfies the required condition, then it is the sum of some subset of $\\left\\{a_{0}, a_{1}, \\ldots, a_{n-1}\\right\\}$; then $c$ is the sum of the complement. Conversely, if $c$ is representable, then its representation consists only of the numbers from $\\left\\{a_{0}, \\ldots, a_{n-1}\\right\\}$, so $a_{n}$ is the sum of the complement. By Claim 2, in order to prove the problem statement, it suffices to find infinitely many representable numbers of the form $2^{t}-3$, as well as infinitely many non-representable ones. Claim 3. For every $t \\geqslant 3$, we have $2^{t}-3 \\sim 2^{4 t-6}-3$, and $2^{4 t-6}-3>2^{t}-3$. Proof. The inequality follows from $t \\geqslant 3$. In order to prove the equivalence, we apply Claim 1 twice in the following manner. First, since $S_{2 t-3}-a_{2 t-2}=2^{t-1}-3<2^{t}-3<2^{2 t-2}+2^{t-1}=a_{2 t-2}$, by Claim 1 we have $2^{t}-3 \\sim S_{2 t-3}-\\left(2^{t}-3\\right)=2^{2 t-2}$. Second, since $S_{4 t-7}-a_{4 t-6}=2^{2 t-3}-3<2^{2 t-2}<2^{4 t-6}+2^{2 t-3}=a_{4 t-6}$, by Claim 1 we have $2^{2 t-2} \\sim S_{4 t-7}-2^{2 t-2}=2^{4 t-6}-3$. Therefore, $2^{t}-3 \\sim 2^{2 t-2} \\sim 2^{4 t-6}-3$, as required. Now it is easy to find the required numbers. Indeed, the number $2^{3}-3=5=a_{0}+a_{1}$ is representable, so Claim 3 provides an infinite sequence of representable numbers $$ 2^{3}-3 \\sim 2^{6}-3 \\sim 2^{18}-3 \\sim \\cdots \\sim 2^{t}-3 \\sim 2^{4 t-6}-3 \\sim \\cdots \\text {. } $$ On the other hand, the number $2^{7}-3=125$ is non-representable (since by Claim 1 we have $125 \\sim S_{6}-125=24 \\sim S_{4}-24=17 \\sim S_{3}-17=4$ which is clearly non-representable). So Claim 3 provides an infinite sequence of non-representable numbers $$ 2^{7}-3 \\sim 2^{22}-3 \\sim 2^{82}-3 \\sim \\cdots \\sim 2^{t}-3 \\sim 2^{4 t-6}-3 \\sim \\cdots . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N3", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Define the sequence $a_{0}, a_{1}, a_{2}, \\ldots$ by $a_{n}=2^{n}+2^{\\lfloor n / 2\\rfloor}$. Prove that there are infinitely many terms of the sequence which can be expressed as a sum of (two or more) distinct terms of the sequence, as well as infinitely many of those which cannot be expressed in such a way. (Serbia)", "solution": "We keep the notion of representability and the notation $S_{n}$ from the previous solution. We say that an index $n$ is good if $a_{n}$ writes as a sum of smaller terms from the sequence $a_{0}, a_{1}, \\ldots$. Otherwise we say it is bad. We must prove that there are infinitely many good indices, as well as infinitely many bad ones. Lemma 1. If $m \\geqslant 0$ is an integer, then $4^{m}$ is representable if and only if either of $2 m+1$ and $2 m+2$ is good. Proof. The case $m=0$ is obvious, so we may assume that $m \\geqslant 1$. Let $n=2 m+1$ or $2 m+2$. Then $n \\geqslant 3$. We notice that $$ S_{n-1}<a_{n-2}+a_{n} $$ The inequality writes as $2^{n}+2^{\\lceil n / 2\\rceil}+2^{\\lfloor n / 2\\rfloor}-3<2^{n}+2^{\\lfloor n / 2\\rfloor}+2^{n-2}+2^{\\lfloor n / 2\\rfloor-1}$, i.e. as $2^{\\lceil n / 2\\rceil}<$ $2^{n-2}+2^{\\lfloor n / 2\\rfloor-1}+3$. If $n \\geqslant 4$, then $n / 2 \\leqslant n-2$, so $\\lceil n / 2\\rceil \\leqslant n-2$ and $2^{\\lceil n / 2\\rceil} \\leqslant 2^{n-2}$. For $n=3$ the inequality verifies separately. If $n$ is good, then $a_{n}$ writes as $a_{n}=a_{i_{1}}+\\cdots+a_{i_{r}}$, where $r \\geqslant 2$ and $i_{1}<\\cdots<i_{r}<n$. Then $i_{r}=n-1$ and $i_{r-1}=n-2$, for if $n-1$ or $n-2$ is missing from the sequence $i_{1}, \\ldots, i_{r}$, then $a_{i_{1}}+\\cdots+a_{i_{r}} \\leqslant a_{0}+\\cdots+a_{n-3}+a_{n-1}=S_{n-1}-a_{n-2}<a_{n}$. Thus, if $n$ is good, then both $a_{n}-a_{n-1}$ and $a_{n}-a_{n-1}-a_{n-2}$ are representable. We now consider the cases $n=2 m+1$ and $n=2 m+2$ separately. If $n=2 m+1$, then $a_{n}-a_{n-1}=a_{2 m+1}-a_{2 m}=\\left(2^{2 m+1}+2^{m}\\right)-\\left(2^{2 m}+2^{m}\\right)=2^{2 m}$. So we proved that, if $2 m+1$ is good, then $2^{2 m}$ is representable. Conversely, if $2^{2 m}$ is representable, then $2^{2 m}<a_{2 m}$, so $2^{2 m}$ is a sum of some distinct terms $a_{i}$ with $i<2 m$. It follows that $a_{2 m+1}=a_{2 m}+2^{2 m}$ writes as $a_{2 m}$ plus a sum of some distinct terms $a_{i}$ with $i<2 m$. Hence $2 m+1$ is good. If $n=2 m+2$, then $a_{n}-a_{n-1}-a_{n-2}=a_{2 m+2}-a_{2 m+1}-a_{2 m}=\\left(2^{2 m+2}+2^{m+1}\\right)-\\left(2^{2 m+1}+\\right.$ $\\left.2^{m}\\right)-\\left(2^{2 m}+2^{m}\\right)=2^{2 m}$. So we proved that, if $2 m+2$ is good, then $2^{2 m}$ is representable. Conversely, if $2^{2 m}$ is representable, then, as seen in the previous case, it writes as a sum of some distinct terms $a_{i}$ with $i<2 m$. Hence $a_{2 m+2}=a_{2 m+1}+a_{2 m}+2^{2 m}$ writes as $a_{2 m+1}+a_{2 m}$ plus a sum of some distinct terms $a_{i}$ with $i<2 m$. Thus $2 m+2$ is good. Lemma 2. If $k \\geqslant 2$, then $2^{4 k-2}$ is representable if and only if $2^{k+1}$ is representable. In particular, if $s \\geqslant 2$, then $4^{s}$ is representable if and only if $4^{4 s-3}$ is representable. Also, $4^{4 s-3}>4^{s}$. Proof. We have $2^{4 k-2}<a_{4 k-2}$, so in a representation of $2^{4 k-2}$ we can have only terms $a_{i}$ with $i \\leqslant 4 k-3$. Notice that $$ a_{0}+\\cdots+a_{4 k-3}=2^{4 k-2}+2^{2 k}-3<2^{4 k-2}+2^{2 k}+2^{k}=2^{4 k-2}+a_{2 k} . $$ Hence, any representation of $2^{4 k-2}$ must contain all terms from $a_{2 k}$ to $a_{4 k-3}$. (If any of these terms is missing, then the sum of the remaining ones is $\\leqslant\\left(a_{0}+\\cdots+a_{4 k-3}\\right)-a_{2 k}<2^{4 k-2}$. Hence, if $2^{4 k-2}$ is representable, then $2^{4 k-2}-\\sum_{i=2 k}^{4 k-3} a_{i}$ is representable. But $2^{4 k-2}-\\sum_{i=2 k}^{4 k-3} a_{i}=2^{4 k-2}-\\left(S_{4 k-3}-S_{2 k-1}\\right)=2^{4 k-2}-\\left(2^{4 k-2}+2^{2 k}-3\\right)+\\left(2^{2 k}+2^{k+1}-3\\right)=2^{k+1}$. So, if $2^{4 k-2}$ is representable, then $2^{k+1}$ is representable. Conversely, if $2^{k+1}$ is representable, then $2^{k+1}<2^{2 k}+2^{k}=a_{2 k}$, so $2^{k+1}$ writes as a sum of some distinct terms $a_{i}$ with $i<2 k$. It follows that $2^{4 k-2}=\\sum_{i=2 k}^{4 k-3} a_{i}+2^{k+1}$ writes as $a_{4 k-3}+a_{4 k-4}+\\cdots+a_{2 k}$ plus the sum of some distinct terms $a_{i}$ with $i<2 k$. Hence $2^{4 k-2}$ is representable. For the second statement, if $s \\geqslant 2$, then we just take $k=2 s-1$ and we notice that $2^{k+1}=4^{s}$ and $2^{4 k-2}=4^{4 s-3}$. Also, $s \\geqslant 2$ implies that $4 s-3>s$. Now $4^{2}=a_{2}+a_{3}$ is representable, whereas $4^{6}=4096$ is not. Indeed, note that $4^{6}=2^{12}<a_{12}$, so the only available terms for a representation are $a_{0}, \\ldots, a_{11}$, i.e., $2,3,6,10,20,36,72$, 136, 272, 528, 1056, 2080. Their sum is $S_{11}=4221$, which exceeds 4096 by 125 . Then any representation of 4096 must contain all the terms from $a_{0}, \\ldots, a_{11}$ that are greater that 125 , i.e., $136,272,528,1056,2080$. Their sum is 4072 . Since $4096-4072=24$ and 24 is clearly not representable, 4096 is non-representable as well. Starting with these values of $m$, by using Lemma 2, we can obtain infinitely many representable powers of 4, as well as infinitely many non-representable ones. By Lemma 1, this solves our problem. This page is intentionally left blank", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N4", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}, \\ldots$ be a sequence of positive integers such that $$ \\frac{a_{1}}{a_{2}}+\\frac{a_{2}}{a_{3}}+\\cdots+\\frac{a_{n-1}}{a_{n}}+\\frac{a_{n}}{a_{1}} $$ is an integer for all $n \\geqslant k$, where $k$ is some positive integer. Prove that there exists a positive integer $m$ such that $a_{n}=a_{n+1}$ for all $n \\geqslant m$. (Mongolia)", "solution": "The argument hinges on the following two facts: Let $a, b, c$ be positive integers such that $N=b / c+(c-b) / a$ is an integer. (1) If $\\operatorname{gcd}(a, c)=1$, then $c$ divides $b$; and (2) If $\\operatorname{gcd}(a, b, c)=1$, then $\\operatorname{gcd}(a, b)=1$. To prove (1), write $a b=c(a N+b-c)$. Since $\\operatorname{gcd}(a, c)=1$, it follows that $c$ divides $b$. To prove (2), write $c^{2}-b c=a(c N-b)$ to infer that $a$ divides $c^{2}-b c$. Letting $d=\\operatorname{gcd}(a, b)$, it follows that $d$ divides $c^{2}$, and since the two are relatively prime by hypothesis, $d=1$. Now, let $s_{n}=a_{1} / a_{2}+a_{2} / a_{3}+\\cdots+a_{n-1} / a_{n}+a_{n} / a_{1}$, let $\\delta_{n}=\\operatorname{gcd}\\left(a_{1}, a_{n}, a_{n+1}\\right)$ and write $$ s_{n+1}-s_{n}=\\frac{a_{n}}{a_{n+1}}+\\frac{a_{n+1}-a_{n}}{a_{1}}=\\frac{a_{n} / \\delta_{n}}{a_{n+1} / \\delta_{n}}+\\frac{a_{n+1} / \\delta_{n}-a_{n} / \\delta_{n}}{a_{1} / \\delta_{n}} . $$ Let $n \\geqslant k$. Since $\\operatorname{gcd}\\left(a_{1} / \\delta_{n}, a_{n} / \\delta_{n}, a_{n+1} / \\delta_{n}\\right)=1$, it follows by (2) that $\\operatorname{gcd}\\left(a_{1} / \\delta_{n}, a_{n} / \\delta_{n}\\right)=1$. Let $d_{n}=\\operatorname{gcd}\\left(a_{1}, a_{n}\\right)$. Then $d_{n}=\\delta_{n} \\cdot \\operatorname{gcd}\\left(a_{1} / \\delta_{n}, a_{n} / \\delta_{n}\\right)=\\delta_{n}$, so $d_{n}$ divides $a_{n+1}$, and therefore $d_{n}$ divides $d_{n+1}$. Consequently, from some rank on, the $d_{n}$ form a nondecreasing sequence of integers not exceeding $a_{1}$, so $d_{n}=d$ for all $n \\geqslant \\ell$, where $\\ell$ is some positive integer. Finally, since $\\operatorname{gcd}\\left(a_{1} / d, a_{n+1} / d\\right)=1$, it follows by (1) that $a_{n+1} / d$ divides $a_{n} / d$, so $a_{n} \\geqslant a_{n+1}$ for all $n \\geqslant \\ell$. The conclusion follows.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N4", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $a_{1}, a_{2}, \\ldots, a_{n}, \\ldots$ be a sequence of positive integers such that $$ \\frac{a_{1}}{a_{2}}+\\frac{a_{2}}{a_{3}}+\\cdots+\\frac{a_{n-1}}{a_{n}}+\\frac{a_{n}}{a_{1}} $$ is an integer for all $n \\geqslant k$, where $k$ is some positive integer. Prove that there exists a positive integer $m$ such that $a_{n}=a_{n+1}$ for all $n \\geqslant m$. (Mongolia)", "solution": "We use the same notation $s_{n}$. This time, we explore the exponents of primes in the prime factorizations of the $a_{n}$ for $n \\geqslant k$. To start, for every $n \\geqslant k$, we know that the number $$ s_{n+1}-s_{n}=\\frac{a_{n}}{a_{n+1}}+\\frac{a_{n+1}}{a_{1}}-\\frac{a_{n}}{a_{1}} $$ is integer. Multiplying it by $a_{1}$ we obtain that $a_{1} a_{n} / a_{n+1}$ is integer as well, so that $a_{n+1} \\mid a_{1} a_{n}$. This means that $a_{n} \\mid a_{1}^{n-k} a_{k}$, so all prime divisors of $a_{n}$ are among those of $a_{1} a_{k}$. There are finitely many such primes; therefore, it suffices to prove that the exponent of each of them in the prime factorization of $a_{n}$ is eventually constant. Choose any prime $p \\mid a_{1} a_{k}$. Recall that $v_{p}(q)$ is the standard notation for the exponent of $p$ in the prime factorization of a nonzero rational number $q$. Say that an index $n \\geqslant k$ is large if $v_{p}\\left(a_{n}\\right) \\geqslant v_{p}\\left(a_{1}\\right)$. We separate two cases. Case 1: There exists a large index $n$. If $v_{p}\\left(a_{n+1}\\right)<v_{p}\\left(a_{1}\\right)$, then $v_{p}\\left(a_{n} / a_{n+1}\\right)$ and $v_{p}\\left(a_{n} / a_{1}\\right)$ are nonnegative, while $v_{p}\\left(a_{n+1} / a_{1}\\right)<0$; hence $(*)$ cannot be an integer. This contradiction shows that index $n+1$ is also large. On the other hand, if $v_{p}\\left(a_{n+1}\\right)>v_{p}\\left(a_{n}\\right)$, then $v_{p}\\left(a_{n} / a_{n+1}\\right)<0$, while $v_{p}\\left(\\left(a_{n+1}-a_{n}\\right) / a_{1}\\right) \\geqslant 0$, so $(*)$ is not integer again. Thus, $v_{p}\\left(a_{1}\\right) \\leqslant v_{p}\\left(a_{n+1}\\right) \\leqslant v_{p}\\left(a_{n}\\right)$. The above arguments can now be applied successively to indices $n+1, n+2, \\ldots$, showing that all the indices greater than $n$ are large, and the sequence $v_{p}\\left(a_{n}\\right), v_{p}\\left(a_{n+1}\\right), v_{p}\\left(a_{n+2}\\right), \\ldots$ is nonincreasing — hence eventually constant. Case 2: There is no large index. We have $v_{p}\\left(a_{1}\\right)>v_{p}\\left(a_{n}\\right)$ for all $n \\geqslant k$. If we had $v_{p}\\left(a_{n+1}\\right)<v_{p}\\left(a_{n}\\right)$ for some $n \\geqslant k$, then $v_{p}\\left(a_{n+1} / a_{1}\\right)<v_{p}\\left(a_{n} / a_{1}\\right)<0<v_{p}\\left(a_{n} / a_{n+1}\\right)$ which would also yield that $(*)$ is not integer. Therefore, in this case the sequence $v_{p}\\left(a_{k}\\right), v_{p}\\left(a_{k+1}\\right), v_{p}\\left(a_{k+2}\\right), \\ldots$ is nondecreasing and bounded by $v_{p}\\left(a_{1}\\right)$ from above; hence it is also eventually constant. Comment. Given any positive odd integer $m$, consider the $m$-tuple $\\left(2,2^{2}, \\ldots, 2^{m-1}, 2^{m}\\right)$. Appending an infinite string of 1 's to this $m$-tuple yields an eventually constant sequence of integers satisfying the condition in the statement, and shows that the rank from which the sequence stabilises may be arbitrarily large. There are more sophisticated examples. The solution to part (b) of 10532, Amer. Math. Monthly, Vol. 105 No. 8 (Oct. 1998), 775-777 (available at https://www.jstor.org/stable/2589009), shows that, for every integer $m \\geqslant 5$, there exists an $m$-tuple $\\left(a_{1}, a_{2}, \\ldots, a_{m}\\right)$ of pairwise distinct positive integers such that $\\operatorname{gcd}\\left(a_{1}, a_{2}\\right)=\\operatorname{gcd}\\left(a_{2}, a_{3}\\right)=\\cdots=\\operatorname{gcd}\\left(a_{m-1}, a_{m}\\right)=\\operatorname{gcd}\\left(a_{m}, a_{1}\\right)=1$, and the sum $a_{1} / a_{2}+a_{2} / a_{3}+\\cdots+a_{m-1} / a_{m}+a_{m} / a_{1}$ is an integer. Letting $a_{m+k}=a_{1}, k=1,2, \\ldots$, extends such an $m$-tuple to an eventually constant sequence of positive integers satisfying the condition in the statement of the problem at hand. Here is the example given by the proposers of 10532. Let $b_{1}=2$, let $b_{k+1}=1+b_{1} \\cdots b_{k}=$ $1+b_{k}\\left(b_{k}-1\\right), k \\geqslant 1$, and set $B_{m}=b_{1} \\cdots b_{m-4}=b_{m-3}-1$. The $m$-tuple $\\left(a_{1}, a_{2}, \\ldots, a_{m}\\right)$ defined below satisfies the required conditions: $$ \\begin{aligned} a_{1}=1, \\quad a_{2} & =\\left(8 B_{m}+1\\right) B_{m}+8, \\quad a_{3}=8 B_{m}+1, \\quad a_{k}=b_{m-k} \\quad \\text { for } 4 \\leqslant k \\leqslant m-1, \\\\ & a_{m}=\\frac{a_{2}}{2} \\cdot a_{3} \\cdot \\frac{B_{m}}{2}=\\left(\\frac{1}{2}\\left(8 B_{m}+1\\right) B_{m}+4\\right) \\cdot\\left(8 B_{m}+1\\right) \\cdot \\frac{B_{m}}{2} . \\end{aligned} $$ It is readily checked that $a_{1}<a_{m-1}<a_{m-2}<\\cdots<a_{3}<a_{2}<a_{m}$. For further details we refer to the solution mentioned above. Acquaintance with this example (or more elaborated examples derived from) offers no advantage in tackling the problem.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N5", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia)", "solution": "Arguing indirectly, assume that $x y=a^{2}$ and $z t=c^{2}$ with $a, c>0$. Suppose that the number $x+y=z+t$ is odd. Then $x$ and $y$ have opposite parity, as well as $z$ and $t$. This means that both $x y$ and $z t$ are even, as well as $x y-z t=x+y$; a contradiction. Thus, $x+y$ is even, so the number $s=\\frac{x+y}{2}=\\frac{z+t}{2}$ is a positive integer. Next, we set $b=\\frac{|x-y|}{2}, d=\\frac{|z-t|}{2}$. Now the problem conditions yield $$ s^{2}=a^{2}+b^{2}=c^{2}+d^{2} $$ and $$ 2 s=a^{2}-c^{2}=d^{2}-b^{2} $$ (the last equality in (2) follows from (1)). We readily get from (2) that $a, d>0$. In the sequel we will use only the relations (1) and (2), along with the fact that $a, d, s$ are positive integers, while $b$ and $c$ are nonnegative integers, at most one of which may be zero. Since both relations are symmetric with respect to the simultaneous swappings $a \\leftrightarrow d$ and $b \\leftrightarrow c$, we assume, without loss of generality, that $b \\geqslant c$ (and hence $b>0$ ). Therefore, $d^{2}=2 s+b^{2}>c^{2}$, whence $$ d^{2}>\\frac{c^{2}+d^{2}}{2}=\\frac{s^{2}}{2} $$ On the other hand, since $d^{2}-b^{2}$ is even by (2), the numbers $b$ and $d$ have the same parity, so $0<b \\leqslant d-2$. Therefore, $$ 2 s=d^{2}-b^{2} \\geqslant d^{2}-(d-2)^{2}=4(d-1), \\quad \\text { i.e., } \\quad d \\leqslant \\frac{s}{2}+1 $$ Combining (3) and (4) we obtain $$ 2 s^{2}<4 d^{2} \\leqslant 4\\left(\\frac{s}{2}+1\\right)^{2}, \\quad \\text { or } \\quad(s-2)^{2}<8 $$ which yields $s \\leqslant 4$. Finally, an easy check shows that each number of the form $s^{2}$ with $1 \\leqslant s \\leqslant 4$ has a unique representation as a sum of two squares, namely $s^{2}=s^{2}+0^{2}$. Thus, (1) along with $a, d>0$ imply $b=c=0$, which is impossible.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N5", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia)", "solution": "We start with a complete description of all 4-tuples $(x, y, z, t)$ of positive integers satisfying (*). As in the solution above, we notice that the numbers $$ s=\\frac{x+y}{2}=\\frac{z+t}{2}, \\quad p=\\frac{x-y}{2}, \\quad \\text { and } \\quad q=\\frac{z-t}{2} $$ are integers (we may, and will, assume that $p, q \\geqslant 0$ ). We have $$ 2 s=x y-z t=(s+p)(s-p)-(s+q)(s-q)=q^{2}-p^{2} $$ so $p$ and $q$ have the same parity, and $q>p$. Set now $k=\\frac{q-p}{2}, \\ell=\\frac{q+p}{2}$. Then we have $s=\\frac{q^{2}-p^{2}}{2}=2 k \\ell$ and hence $$ \\begin{array}{rlrl} x & =s+p=2 k \\ell-k+\\ell, & y & =s-p=2 k \\ell+k-\\ell, \\\\ z & =s+q=2 k \\ell+k+\\ell, & t=s-q=2 k \\ell-k-\\ell . \\end{array} $$ Recall here that $\\ell \\geqslant k>0$ and, moreover, $(k, \\ell) \\neq(1,1)$, since otherwise $t=0$. Assume now that both $x y$ and $z t$ are squares. Then $x y z t$ is also a square. On the other hand, we have $$ \\begin{aligned} x y z t=(2 k \\ell-k+\\ell) & (2 k \\ell+k-\\ell)(2 k \\ell+k+\\ell)(2 k \\ell-k-\\ell) \\\\ & =\\left(4 k^{2} \\ell^{2}-(k-\\ell)^{2}\\right)\\left(4 k^{2} \\ell^{2}-(k+\\ell)^{2}\\right)=\\left(4 k^{2} \\ell^{2}-k^{2}-\\ell^{2}\\right)^{2}-4 k^{2} \\ell^{2} \\end{aligned} $$ Denote $D=4 k^{2} \\ell^{2}-k^{2}-\\ell^{2}>0$. From (6) we get $D^{2}>x y z t$. On the other hand, $$ \\begin{array}{r} (D-1)^{2}=D^{2}-2\\left(4 k^{2} \\ell^{2}-k^{2}-\\ell^{2}\\right)+1=\\left(D^{2}-4 k^{2} \\ell^{2}\\right)-\\left(2 k^{2}-1\\right)\\left(2 \\ell^{2}-1\\right)+2 \\\\ =x y z t-\\left(2 k^{2}-1\\right)\\left(2 \\ell^{2}-1\\right)+2<x y z t \\end{array} $$ since $\\ell \\geqslant 2$ and $k \\geqslant 1$. Thus $(D-1)^{2}<x y z t<D^{2}$, and $x y z t$ cannot be a perfect square; a contradiction. Comment. The first part of Solution 2 shows that all 4-tuples of positive integers $x \\geqslant y, z \\geqslant t$ satisfying (*) have the form (5), where $\\ell \\geqslant k>0$ and $\\ell \\geqslant 2$. The converse is also true: every pair of positive integers $\\ell \\geqslant k>0$, except for the pair $k=\\ell=1$, generates via (5) a 4-tuple of positive integers satisfying $(*)$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N6", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $f:\\{1,2,3, \\ldots\\} \\rightarrow\\{2,3, \\ldots\\}$ be a function such that $f(m+n) \\mid f(m)+f(n)$ for all pairs $m, n$ of positive integers. Prove that there exists a positive integer $c>1$ which divides all values of $f$. (Mexico)", "solution": "For every positive integer $m$, define $S_{m}=\\{n: m \\mid f(n)\\}$. Lemma. If the set $S_{m}$ is infinite, then $S_{m}=\\{d, 2 d, 3 d, \\ldots\\}=d \\cdot \\mathbb{Z}_{>0}$ for some positive integer $d$. Proof. Let $d=\\min S_{m}$; the definition of $S_{m}$ yields $m \\mid f(d)$. Whenever $n \\in S_{m}$ and $n>d$, we have $m|f(n)| f(n-d)+f(d)$, so $m \\mid f(n-d)$ and therefore $n-d \\in S_{m}$. Let $r \\leqslant d$ be the least positive integer with $n \\equiv r(\\bmod d)$; repeating the same step, we can see that $n-d, n-2 d, \\ldots, r \\in S_{m}$. By the minimality of $d$, this shows $r=d$ and therefore $d \\mid n$. Starting from an arbitrarily large element of $S_{m}$, the process above reaches all multiples of $d$; so they all are elements of $S_{m}$. The solution for the problem will be split into two cases. Case 1: The function $f$ is bounded. Call a prime $p$ frequent if the set $S_{p}$ is infinite, i.e., if $p$ divides $f(n)$ for infinitely many positive integers $n$; otherwise call $p$ sporadic. Since the function $f$ is bounded, there are only a finite number of primes that divide at least one $f(n)$; so altogether there are finitely many numbers $n$ such that $f(n)$ has a sporadic prime divisor. Let $N$ be a positive integer, greater than all those numbers $n$. Let $p_{1}, \\ldots, p_{k}$ be the frequent primes. By the lemma we have $S_{p_{i}}=d_{i} \\cdot \\mathbb{Z}_{>0}$ for some $d_{i}$. Consider the number $$ n=N d_{1} d_{2} \\cdots d_{k}+1 $$ Due to $n>N$, all prime divisors of $f(n)$ are frequent primes. Let $p_{i}$ be any frequent prime divisor of $f(n)$. Then $n \\in S_{p_{i}}$, and therefore $d_{i} \\mid n$. But $n \\equiv 1\\left(\\bmod d_{i}\\right)$, which means $d_{i}=1$. Hence $S_{p_{i}}=1 \\cdot \\mathbb{Z}_{>0}=\\mathbb{Z}_{>0}$ and therefore $p_{i}$ is a common divisor of all values $f(n)$. Case 2: $f$ is unbounded. We prove that $f(1)$ divides all $f(n)$. Let $a=f(1)$. Since $1 \\in S_{a}$, by the lemma it suffices to prove that $S_{a}$ is an infinite set. Call a positive integer $p$ a peak if $f(p)>\\max (f(1), \\ldots, f(p-1))$. Since $f$ is not bounded, there are infinitely many peaks. Let $1=p_{1}<p_{2}<\\ldots$ be the sequence of all peaks, and let $h_{k}=f\\left(p_{k}\\right)$. Notice that for any peak $p_{i}$ and for any $k<p_{i}$, we have $f\\left(p_{i}\\right) \\mid f(k)+f\\left(p_{i}-k\\right)<$ $2 f\\left(p_{i}\\right)$, hence $$ f(k)+f\\left(p_{i}-k\\right)=f\\left(p_{i}\\right)=h_{i} . $$ By the pigeonhole principle, among the numbers $h_{1}, h_{2}, \\ldots$ there are infinitely many that are congruent modulo $a$. Let $k_{0}<k_{1}<k_{2}<\\ldots$ be an infinite sequence of positive integers such that $h_{k_{0}} \\equiv h_{k_{1}} \\equiv \\ldots(\\bmod a)$. Notice that $$ f\\left(p_{k_{i}}-p_{k_{0}}\\right)=f\\left(p_{k_{i}}\\right)-f\\left(p_{k_{0}}\\right)=h_{k_{i}}-h_{k_{0}} \\equiv 0 \\quad(\\bmod a), $$ so $p_{k_{i}}-p_{k_{0}} \\in S_{a}$ for all $i=1,2, \\ldots$ This provides infinitely many elements in $S_{a}$. Hence, $S_{a}$ is an infinite set, and therefore $f(1)=a$ divides $f(n)$ for every $n$. Comment. As an extension of the solution above, it can be proven that if $f$ is not bounded then $f(n)=a n$ with $a=f(1)$. Take an arbitrary positive integer $n$; we will show that $f(n+1)=f(n)+a$. Then it follows by induction that $f(n)=a n$. Take a peak $p$ such that $p>n+2$ and $h=f(p)>f(n)+2 a$. By (1) we have $f(p-1)=$ $f(p)-f(1)=h-a$ and $f(n+1)=f(p)-f(p-n-1)=h-f(p-n-1)$. From $h-a=f(p-1) \\mid$ $f(n)+f(p-n-1)<f(n)+h<2(h-a)$ we get $f(n)+f(p-n-1)=h-a$. Then $$ f(n+1)-f(n)=(h-f(p-n-1))-(h-a-f(p-n-1))=a . $$ On the other hand, there exists a wide family of bounded functions satisfying the required properties. Here we present a few examples: $$ f(n)=c ; \\quad f(n)=\\left\\{\\begin{array}{ll} 2 c & \\text { if } n \\text { is even } \\\\ c & \\text { if } n \\text { is odd; } \\end{array} \\quad f(n)= \\begin{cases}2018 c & \\text { if } n \\leqslant 2018 \\\\ c & \\text { if } n>2018\\end{cases}\\right. $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N6", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $f:\\{1,2,3, \\ldots\\} \\rightarrow\\{2,3, \\ldots\\}$ be a function such that $f(m+n) \\mid f(m)+f(n)$ for all pairs $m, n$ of positive integers. Prove that there exists a positive integer $c>1$ which divides all values of $f$. (Mexico)", "solution": "Let $d_{n}=\\operatorname{gcd}(f(n), f(1))$. From $d_{n+1} \\mid f(1)$ and $d_{n+1}|f(n+1)| f(n)+f(1)$, we can see that $d_{n+1} \\mid f(n)$; then $d_{n+1} \\mid \\operatorname{gcd}(f(n), f(1))=d_{n}$. So the sequence $d_{1}, d_{2}, \\ldots$ is nonincreasing in the sense that every element is a divisor of the previous elements. Let $d=\\min \\left(d_{1}, d_{2}, \\ldots\\right)=\\operatorname{gcd}\\left(d_{1} \\cdot d_{2}, \\ldots\\right)=\\operatorname{gcd}(f(1), f(2), \\ldots)$; we have to prove $d \\geqslant 2$. For the sake of contradiction, suppose that the statement is wrong, so $d=1$; that means there is some index $n_{0}$ such that $d_{n}=1$ for every $n \\geqslant n_{0}$, i.e., $f(n)$ is coprime with $f(1)$. Claim 1. If $2^{k} \\geqslant n_{0}$ then $f\\left(2^{k}\\right) \\leqslant 2^{k}$. Proof. By the condition, $f(2 n) \\mid 2 f(n)$; a trivial induction yields $f\\left(2^{k}\\right) \\mid 2^{k} f(1)$. If $2^{k} \\geqslant n_{0}$ then $f\\left(2^{k}\\right)$ is coprime with $f(1)$, so $f\\left(2^{k}\\right)$ is a divisor of $2^{k}$. Claim 2. There is a constant $C$ such that $f(n)<n+C$ for every $n$. Proof. Take the first power of 2 which is greater than or equal to $n_{0}$ : let $K=2^{k} \\geqslant n_{0}$. By Claim 1, we have $f(K) \\leqslant K$. Notice that $f(n+K) \\mid f(n)+f(K)$ implies $f(n+K) \\leqslant$ $f(n)+f(K) \\leqslant f(n)+K$. If $n=t K+r$ for some $t \\geqslant 0$ and $1 \\leqslant r \\leqslant K$, then we conclude $f(n) \\leqslant K+f(n-K) \\leqslant 2 K+f(n-2 K) \\leqslant \\ldots \\leqslant t K+f(r)<n+\\max (f(1), f(2), \\ldots, f(K))$, so the claim is true with $C=\\max (f(1), \\ldots, f(K))$. Claim 3. If $a, b \\in \\mathbb{Z}_{>0}$ are coprime then $\\operatorname{gcd}(f(a), f(b)) \\mid f(1)$. In particular, if $a, b \\geqslant n_{0}$ are coprime then $f(a)$ and $f(b)$ are coprime. Proof. Let $d=\\operatorname{gcd}(f(a), f(b))$. We can replicate Euclid's algorithm. Formally, apply induction on $a+b$. If $a=1$ or $b=1$ then we already have $d \\mid f(1)$. Without loss of generality, suppose $1<a<b$. Then $d \\mid f(a)$ and $d|f(b)| f(a)+f(b-a)$, so $d \\mid f(b-a)$. Therefore $d$ divides $\\operatorname{gcd}(f(a), f(b-a))$ which is a divisor of $f(1)$ by the induction hypothesis. Let $p_{1}<p_{2}<\\ldots$ be the sequence of all prime numbers; for every $k$, let $q_{k}$ be the lowest power of $p_{k}$ with $q_{k} \\geqslant n_{0}$. (Notice that there are only finitely many positive integers with $q_{k} \\neq p_{k}$.) Take a positive integer $N$, and consider the numbers $$ f(1), f\\left(q_{1}\\right), f\\left(q_{2}\\right), \\ldots, f\\left(q_{N}\\right) $$ Here we have $N+1$ numbers, each being greater than 1 , and they are pairwise coprime by Claim 3. Therefore, they have at least $N+1$ different prime divisors in total, and their greatest prime divisor is at least $p_{N+1}$. Hence, $\\max \\left(f(1), f\\left(q_{1}\\right), \\ldots, f\\left(q_{N}\\right)\\right) \\geqslant p_{N+1}$. Choose $N$ such that $\\max \\left(q_{1}, \\ldots, q_{N}\\right)=p_{N}$ (this is achieved if $N$ is sufficiently large), and $p_{N+1}-p_{N}>C$ (that is possible, because there are arbitrarily long gaps between the primes). Then we establish a contradiction $$ p_{N+1} \\leqslant \\max \\left(f(1), f\\left(q_{1}\\right), \\ldots, f\\left(q_{N}\\right)\\right)<\\max \\left(1+C, q_{1}+C, \\ldots, q_{N}+C\\right)=p_{N}+C<p_{N+1} $$ which proves the statement.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N7", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $n \\geqslant 2018$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}, b_{1}, b_{2}, \\ldots, b_{n}$ be pairwise distinct positive integers not exceeding $5 n$. Suppose that the sequence $$ \\frac{a_{1}}{b_{1}}, \\frac{a_{2}}{b_{2}}, \\ldots, \\frac{a_{n}}{b_{n}} $$ forms an arithmetic progression. Prove that the terms of the sequence are equal.", "solution": "Suppose that (1) is an arithmetic progression with nonzero difference. Let the difference be $\\Delta=\\frac{c}{d}$, where $d>0$ and $c, d$ are coprime. We will show that too many denominators $b_{i}$ should be divisible by $d$. To this end, for any $1 \\leqslant i \\leqslant n$ and any prime divisor $p$ of $d$, say that the index $i$ is $p$-wrong, if $v_{p}\\left(b_{i}\\right)<v_{p}(d)$. $\\left(v_{p}(x)\\right.$ stands for the exponent of $p$ in the prime factorisation of $x$.) Claim 1. For any prime $p$, all $p$-wrong indices are congruent modulo $p$. In other words, the $p$-wrong indices (if they exist) are included in an arithmetic progression with difference $p$. Proof. Let $\\alpha=v_{p}(d)$. For the sake of contradiction, suppose that $i$ and $j$ are $p$-wrong indices (i.e., none of $b_{i}$ and $b_{j}$ is divisible by $\\left.p^{\\alpha}\\right)$ such that $i \\not \\equiv j(\\bmod p)$. Then the least common denominator of $\\frac{a_{i}}{b_{i}}$ and $\\frac{a_{j}}{b_{j}}$ is not divisible by $p^{\\alpha}$. But this is impossible because in their difference, $(i-j) \\Delta=\\frac{(i-j) c}{d}$, the numerator is coprime to $p$, but $p^{\\alpha}$ divides the denominator $d$. Claim 2. $d$ has no prime divisors greater than 5 . Proof. Suppose that $p \\geqslant 7$ is a prime divisor of $d$. Among the indices $1,2, \\ldots, n$, at most $\\left\\lceil\\frac{n}{p}\\right\\rceil<\\frac{n}{p}+1$ are $p$-wrong, so $p$ divides at least $\\frac{p-1}{p} n-1$ of $b_{1}, \\ldots, b_{n}$. Since these denominators are distinct, $$ 5 n \\geqslant \\max \\left\\{b_{i}: p \\mid b_{i}\\right\\} \\geqslant\\left(\\frac{p-1}{p} n-1\\right) p=(p-1)(n-1)-1 \\geqslant 6(n-1)-1>5 n, $$ a contradiction. Claim 3. For every $0 \\leqslant k \\leqslant n-30$, among the denominators $b_{k+1}, b_{k+2}, \\ldots, b_{k+30}$, at least $\\varphi(30)=8$ are divisible by $d$. Proof. By Claim 1, the 2 -wrong, 3 -wrong and 5 -wrong indices can be covered by three arithmetic progressions with differences 2,3 and 5 . By a simple inclusion-exclusion, $(2-1) \\cdot(3-1) \\cdot(5-1)=8$ indices are not covered; by Claim 2, we have $d \\mid b_{i}$ for every uncovered index $i$. Claim 4. $|\\Delta|<\\frac{20}{n-2}$ and $d>\\frac{n-2}{20}$. Proof. From the sequence (1), remove all fractions with $b_{n}<\\frac{n}{2}$, There remain at least $\\frac{n}{2}$ fractions, and they cannot exceed $\\frac{5 n}{n / 2}=10$. So we have at least $\\frac{n}{2}$ elements of the arithmetic progression (1) in the interval $(0,10]$, hence the difference must be below $\\frac{10}{n / 2-1}=\\frac{20}{n-2}$. The second inequality follows from $\\frac{1}{d} \\leqslant \\frac{|c|}{d}=|\\Delta|$. Now we have everything to get the final contradiction. By Claim 3, we have $d \\mid b_{i}$ for at least $\\left\\lfloor\\frac{n}{30}\\right\\rfloor \\cdot 8$ indices $i$. By Claim 4 , we have $d \\geqslant \\frac{n-2}{20}$. Therefore, $$ 5 n \\geqslant \\max \\left\\{b_{i}: d \\mid b_{i}\\right\\} \\geqslant\\left(\\left\\lfloor\\frac{n}{30}\\right\\rfloor \\cdot 8\\right) \\cdot d>\\left(\\frac{n}{30}-1\\right) \\cdot 8 \\cdot \\frac{n-2}{20}>5 n . $$ Comment 1. It is possible that all terms in (1) are equal, for example with $a_{i}=2 i-1$ and $b_{i}=4 i-2$ we have $\\frac{a_{i}}{b_{i}}=\\frac{1}{2}$. Comment 2. The bound $5 n$ in the statement is far from sharp; the solution above can be modified to work for $9 n$. For large $n$, the bound $5 n$ can be replaced by $n^{\\frac{3}{2}-\\varepsilon}$. The activities of the Problem Selection Committee were supported by DEDEMAN LA FANTANA vine la tine", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A1", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $\\mathbb{Q}_{>0}$ denote the set of all positive rational numbers. Determine all functions $f: \\mathbb{Q}_{>0} \\rightarrow \\mathbb{Q}_{>0}$ satisfying $$ f\\left(x^{2} f(y)^{2}\\right)=f(x)^{2} f(y) $$ for all $x, y \\in \\mathbb{Q}_{>0}$. (Switzerland) Answer: $f(x)=1$ for all $x \\in \\mathbb{Q}_{>0}$.", "solution": "Take any $a, b \\in \\mathbb{Q}_{>0}$. By substituting $x=f(a), y=b$ and $x=f(b), y=a$ into $(*)$ we get $$ f(f(a))^{2} f(b)=f\\left(f(a)^{2} f(b)^{2}\\right)=f(f(b))^{2} f(a) $$ which yields $$ \\frac{f(f(a))^{2}}{f(a)}=\\frac{f(f(b))^{2}}{f(b)} \\quad \\text { for all } a, b \\in \\mathbb{Q}_{>0} $$ In other words, this shows that there exists a constant $C \\in \\mathbb{Q}_{>0}$ such that $f(f(a))^{2}=C f(a)$, or $$ \\left(\\frac{f(f(a))}{C}\\right)^{2}=\\frac{f(a)}{C} \\quad \\text { for all } a \\in \\mathbb{Q}_{>0} \\text {. } $$ Denote by $f^{n}(x)=\\underbrace{f(f(\\ldots(f}_{n}(x)) \\ldots))$ the $n^{\\text {th }}$ iteration of $f$. Equality (1) yields $$ \\frac{f(a)}{C}=\\left(\\frac{f^{2}(a)}{C}\\right)^{2}=\\left(\\frac{f^{3}(a)}{C}\\right)^{4}=\\cdots=\\left(\\frac{f^{n+1}(a)}{C}\\right)^{2^{n}} $$ for all positive integer $n$. So, $f(a) / C$ is the $2^{n}$-th power of a rational number for all positive integer $n$. This is impossible unless $f(a) / C=1$, since otherwise the exponent of some prime in the prime decomposition of $f(a) / C$ is not divisible by sufficiently large powers of 2 . Therefore, $f(a)=C$ for all $a \\in \\mathbb{Q}_{>0}$. Finally, after substituting $f \\equiv C$ into (*) we get $C=C^{3}$, whence $C=1$. So $f(x) \\equiv 1$ is the unique function satisfying $(*)$. Comment 1. There are several variations of the solution above. For instance, one may start with finding $f(1)=1$. To do this, let $d=f(1)$. By substituting $x=y=1$ and $x=d^{2}, y=1$ into (*) we get $f\\left(d^{2}\\right)=d^{3}$ and $f\\left(d^{6}\\right)=f\\left(d^{2}\\right)^{2} \\cdot d=d^{7}$. By substituting now $x=1, y=d^{2}$ we obtain $f\\left(d^{6}\\right)=d^{2} \\cdot d^{3}=d^{5}$. Therefore, $d^{7}=f\\left(d^{6}\\right)=d^{5}$, whence $d=1$. After that, the rest of the solution simplifies a bit, since we already know that $C=\\frac{f(f(1))^{2}}{f(1)}=1$. Hence equation (1) becomes merely $f(f(a))^{2}=f(a)$, which yields $f(a)=1$ in a similar manner. Comment 2. There exist nonconstant functions $f: \\mathbb{R}^{+} \\rightarrow \\mathbb{R}^{+}$satisfying $(*)$ for all real $x, y>0-$ e.g., $f(x)=\\sqrt{x}$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A2", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find all positive integers $n \\geqslant 3$ for which there exist real numbers $a_{1}, a_{2}, \\ldots, a_{n}$, $a_{n+1}=a_{1}, a_{n+2}=a_{2}$ such that $$ a_{i} a_{i+1}+1=a_{i+2} $$ for all $i=1,2, \\ldots, n$. (Slovakia) Answer: $n$ can be any multiple of 3 .", "solution": "For the sake of convenience, extend the sequence $a_{1}, \\ldots, a_{n+2}$ to an infinite periodic sequence with period $n$. ( $n$ is not necessarily the shortest period.) If $n$ is divisible by 3 , then $\\left(a_{1}, a_{2}, \\ldots\\right)=(-1,-1,2,-1,-1,2, \\ldots)$ is an obvious solution. We will show that in every periodic sequence satisfying the recurrence, each positive term is followed by two negative values, and after them the next number is positive again. From this, it follows that $n$ is divisible by 3 . If the sequence contains two consecutive positive numbers $a_{i}, a_{i+1}$, then $a_{i+2}=a_{i} a_{i+1}+1>1$, so the next value is positive as well; by induction, all numbers are positive and greater than 1 . But then $a_{i+2}=a_{i} a_{i+1}+1 \\geqslant 1 \\cdot a_{i+1}+1>a_{i+1}$ for every index $i$, which is impossible: our sequence is periodic, so it cannot increase everywhere. If the number 0 occurs in the sequence, $a_{i}=0$ for some index $i$, then it follows that $a_{i+1}=a_{i-1} a_{i}+1$ and $a_{i+2}=a_{i} a_{i+1}+1$ are two consecutive positive elements in the sequences and we get the same contradiction again. Notice that after any two consecutive negative numbers the next one must be positive: if $a_{i}<0$ and $a_{i+1}<0$, then $a_{i+2}=a_{1} a_{i+1}+1>1>0$. Hence, the positive and negative numbers follow each other in such a way that each positive term is followed by one or two negative values and then comes the next positive term. Consider the case when the positive and negative values alternate. So, if $a_{i}$ is a negative value then $a_{i+1}$ is positive, $a_{i+2}$ is negative and $a_{i+3}$ is positive again. Notice that $a_{i} a_{i+1}+1=a_{i+2}<0<a_{i+3}=a_{i+1} a_{i+2}+1$; by $a_{i+1}>0$ we conclude $a_{i}<a_{i+2}$. Hence, the negative values form an infinite increasing subsequence, $a_{i}<a_{i+2}<a_{i+4}<\\ldots$, which is not possible, because the sequence is periodic. The only case left is when there are consecutive negative numbers in the sequence. Suppose that $a_{i}$ and $a_{i+1}$ are negative; then $a_{i+2}=a_{i} a_{i+1}+1>1$. The number $a_{i+3}$ must be negative. We show that $a_{i+4}$ also must be negative. Notice that $a_{i+3}$ is negative and $a_{i+4}=a_{i+2} a_{i+3}+1<1<a_{i} a_{i+1}+1=a_{i+2}$, so $$ a_{i+5}-a_{i+4}=\\left(a_{i+3} a_{i+4}+1\\right)-\\left(a_{i+2} a_{i+3}+1\\right)=a_{i+3}\\left(a_{i+4}-a_{i+2}\\right)>0, $$ therefore $a_{i+5}>a_{i+4}$. Since at most one of $a_{i+4}$ and $a_{i+5}$ can be positive, that means that $a_{i+4}$ must be negative. Now $a_{i+3}$ and $a_{i+4}$ are negative and $a_{i+5}$ is positive; so after two negative and a positive terms, the next three terms repeat the same pattern. That completes the solution.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A2", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find all positive integers $n \\geqslant 3$ for which there exist real numbers $a_{1}, a_{2}, \\ldots, a_{n}$, $a_{n+1}=a_{1}, a_{n+2}=a_{2}$ such that $$ a_{i} a_{i+1}+1=a_{i+2} $$ for all $i=1,2, \\ldots, n$. (Slovakia) Answer: $n$ can be any multiple of 3 .", "solution": "We prove that the shortest period of the sequence must be 3 . Then it follows that $n$ must be divisible by 3 . Notice that the equation $x^{2}+1=x$ has no real root, so the numbers $a_{1}, \\ldots, a_{n}$ cannot be all equal, hence the shortest period of the sequence cannot be 1 . By applying the recurrence relation for $i$ and $i+1$, $$ \\begin{gathered} \\left(a_{i+2}-1\\right) a_{i+2}=a_{i} a_{i+1} a_{i+2}=a_{i}\\left(a_{i+3}-1\\right), \\quad \\text { so } \\\\ a_{i+2}^{2}-a_{i} a_{i+3}=a_{i+2}-a_{i} . \\end{gathered} $$ By summing over $i=1,2, \\ldots, n$, we get $$ \\sum_{i=1}^{n}\\left(a_{i}-a_{i+3}\\right)^{2}=0 $$ That proves that $a_{i}=a_{i+3}$ for every index $i$, so the sequence $a_{1}, a_{2}, \\ldots$ is indeed periodic with period 3. The shortest period cannot be 1 , so it must be 3 ; therefore, $n$ is divisible by 3 . Comment. By solving the system of equations $a b+1=c, \\quad b c+1=a, \\quad c a+1=b$, it can be seen that the pattern $(-1,-1,2)$ is repeated in all sequences satisfying the problem conditions.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A3", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Given any set $S$ of positive integers, show that at least one of the following two assertions holds: (1) There exist distinct finite subsets $F$ and $G$ of $S$ such that $\\sum_{x \\in F} 1 / x=\\sum_{x \\in G} 1 / x$; (2) There exists a positive rational number $r<1$ such that $\\sum_{x \\in F} 1 / x \\neq r$ for all finite subsets $F$ of $S$. ## (Luxembourg)", "solution": "Argue indirectly. Agree, as usual, that the empty sum is 0 to consider rationals in $[0,1)$; adjoining 0 causes no harm, since $\\sum_{x \\in F} 1 / x=0$ for no nonempty finite subset $F$ of $S$. For every rational $r$ in $[0,1)$, let $F_{r}$ be the unique finite subset of $S$ such that $\\sum_{x \\in F_{r}} 1 / x=r$. The argument hinges on the lemma below. Lemma. If $x$ is a member of $S$ and $q$ and $r$ are rationals in $[0,1)$ such that $q-r=1 / x$, then $x$ is a member of $F_{q}$ if and only if it is not one of $F_{r}$. Proof. If $x$ is a member of $F_{q}$, then $$ \\sum_{y \\in F_{q} \\backslash\\{x\\}} \\frac{1}{y}=\\sum_{y \\in F_{q}} \\frac{1}{y}-\\frac{1}{x}=q-\\frac{1}{x}=r=\\sum_{y \\in F_{r}} \\frac{1}{y} $$ so $F_{r}=F_{q} \\backslash\\{x\\}$, and $x$ is not a member of $F_{r}$. Conversely, if $x$ is not a member of $F_{r}$, then $$ \\sum_{y \\in F_{r} \\cup\\{x\\}} \\frac{1}{y}=\\sum_{y \\in F_{r}} \\frac{1}{y}+\\frac{1}{x}=r+\\frac{1}{x}=q=\\sum_{y \\in F_{q}} \\frac{1}{y} $$ so $F_{q}=F_{r} \\cup\\{x\\}$, and $x$ is a member of $F_{q}$. Consider now an element $x$ of $S$ and a positive rational $r<1$. Let $n=\\lfloor r x\\rfloor$ and consider the sets $F_{r-k / x}, k=0, \\ldots, n$. Since $0 \\leqslant r-n / x<1 / x$, the set $F_{r-n / x}$ does not contain $x$, and a repeated application of the lemma shows that the $F_{r-(n-2 k) / x}$ do not contain $x$, whereas the $F_{r-(n-2 k-1) / x}$ do. Consequently, $x$ is a member of $F_{r}$ if and only if $n$ is odd. Finally, consider $F_{2 / 3}$. By the preceding, $\\lfloor 2 x / 3\\rfloor$ is odd for each $x$ in $F_{2 / 3}$, so $2 x / 3$ is not integral. Since $F_{2 / 3}$ is finite, there exists a positive rational $\\varepsilon$ such that $\\lfloor(2 / 3-\\varepsilon) x\\rfloor=\\lfloor 2 x / 3\\rfloor$ for all $x$ in $F_{2 / 3}$. This implies that $F_{2 / 3}$ is a subset of $F_{2 / 3-\\varepsilon}$ which is impossible. Comment. The solution above can be adapted to show that the problem statement still holds, if the condition $r<1$ in (2) is replaced with $r<\\delta$, for an arbitrary positive $\\delta$. This yields that, if $S$ does not satisfy (1), then there exist infinitely many positive rational numbers $r<1$ such that $\\sum_{x \\in F} 1 / x \\neq r$ for all finite subsets $F$ of $S$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A3", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Given any set $S$ of positive integers, show that at least one of the following two assertions holds: (1) There exist distinct finite subsets $F$ and $G$ of $S$ such that $\\sum_{x \\in F} 1 / x=\\sum_{x \\in G} 1 / x$; (2) There exists a positive rational number $r<1$ such that $\\sum_{x \\in F} 1 / x \\neq r$ for all finite subsets $F$ of $S$. ## (Luxembourg)", "solution": "A finite $S$ clearly satisfies (2), so let $S$ be infinite. If $S$ fails both conditions, so does $S \\backslash\\{1\\}$. We may and will therefore assume that $S$ consists of integers greater than 1 . Label the elements of $S$ increasingly $x_{1}<x_{2}<\\cdots$, where $x_{1} \\geqslant 2$. We first show that $S$ satisfies (2) if $x_{n+1} \\geqslant 2 x_{n}$ for all $n$. In this case, $x_{n} \\geqslant 2^{n-1} x_{1}$ for all $n$, so $$ s=\\sum_{n \\geqslant 1} \\frac{1}{x_{n}} \\leqslant \\sum_{n \\geqslant 1} \\frac{1}{2^{n-1} x_{1}}=\\frac{2}{x_{1}} $$ If $x_{1} \\geqslant 3$, or $x_{1}=2$ and $x_{n+1}>2 x_{n}$ for some $n$, then $\\sum_{x \\in F} 1 / x<s<1$ for every finite subset $F$ of $S$, so $S$ satisfies (2); and if $x_{1}=2$ and $x_{n+1}=2 x_{n}$ for all $n$, that is, $x_{n}=2^{n}$ for all $n$, then every finite subset $F$ of $S$ consists of powers of 2 , so $\\sum_{x \\in F} 1 / x \\neq 1 / 3$ and again $S$ satisfies (2). Finally, we deal with the case where $x_{n+1}<2 x_{n}$ for some $n$. Consider the positive rational $r=1 / x_{n}-1 / x_{n+1}<1 / x_{n+1}$. If $r=\\sum_{x \\in F} 1 / x$ for no finite subset $F$ of $S$, then $S$ satisfies (2). We now assume that $r=\\sum_{x \\in F_{0}} 1 / x$ for some finite subset $F_{0}$ of $S$, and show that $S$ satisfies (1). Since $\\sum_{x \\in F_{0}} 1 / x=r<1 / x_{n+1}$, it follows that $x_{n+1}$ is not a member of $F_{0}$, so $$ \\sum_{x \\in F_{0} \\cup\\left\\{x_{n+1}\\right\\}} \\frac{1}{x}=\\sum_{x \\in F_{0}} \\frac{1}{x}+\\frac{1}{x_{n+1}}=r+\\frac{1}{x_{n+1}}=\\frac{1}{x_{n}} $$ Consequently, $F=F_{0} \\cup\\left\\{x_{n+1}\\right\\}$ and $G=\\left\\{x_{n}\\right\\}$ are distinct finite subsets of $S$ such that $\\sum_{x \\in F} 1 / x=\\sum_{x \\in G} 1 / x$, and $S$ satisfies (1).", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A4", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $a_{0}, a_{1}, a_{2}, \\ldots$ be a sequence of real numbers such that $a_{0}=0, a_{1}=1$, and for every $n \\geqslant 2$ there exists $1 \\leqslant k \\leqslant n$ satisfying $$ a_{n}=\\frac{a_{n-1}+\\cdots+a_{n-k}}{k} $$ Find the maximal possible value of $a_{2018}-a_{2017}$. (Belgium) Answer: The maximal value is $\\frac{2016}{2017^{2}}$.", "solution": "The claimed maximal value is achieved at $$ \\begin{gathered} a_{1}=a_{2}=\\cdots=a_{2016}=1, \\quad a_{2017}=\\frac{a_{2016}+\\cdots+a_{0}}{2017}=1-\\frac{1}{2017}, \\\\ a_{2018}=\\frac{a_{2017}+\\cdots+a_{1}}{2017}=1-\\frac{1}{2017^{2}} . \\end{gathered} $$ Now we need to show that this value is optimal. For brevity, we use the notation $$ S(n, k)=a_{n-1}+a_{n-2}+\\cdots+a_{n-k} \\quad \\text { for nonnegative integers } k \\leqslant n \\text {. } $$ In particular, $S(n, 0)=0$ and $S(n, 1)=a_{n-1}$. In these terms, for every integer $n \\geqslant 2$ there exists a positive integer $k \\leqslant n$ such that $a_{n}=S(n, k) / k$. For every integer $n \\geqslant 1$ we define $$ M_{n}=\\max _{1 \\leqslant k \\leqslant n} \\frac{S(n, k)}{k}, \\quad m_{n}=\\min _{1 \\leqslant k \\leqslant n} \\frac{S(n, k)}{k}, \\quad \\text { and } \\quad \\Delta_{n}=M_{n}-m_{n} \\geqslant 0 . $$ By definition, $a_{n} \\in\\left[m_{n}, M_{n}\\right]$ for all $n \\geqslant 2$; on the other hand, $a_{n-1}=S(n, 1) / 1 \\in\\left[m_{n}, M_{n}\\right]$. Therefore, $$ a_{2018}-a_{2017} \\leqslant M_{2018}-m_{2018}=\\Delta_{2018}, $$ and we are interested in an upper bound for $\\Delta_{2018}$. Also by definition, for any $0<k \\leqslant n$ we have $k m_{n} \\leqslant S(n, k) \\leqslant k M_{n}$; notice that these inequalities are also valid for $k=0$. Claim 1. For every $n>2$, we have $\\Delta_{n} \\leqslant \\frac{n-1}{n} \\Delta_{n-1}$. Proof. Choose positive integers $k, \\ell \\leqslant n$ such that $M_{n}=S(n, k) / k$ and $m_{n}=S(n, \\ell) / \\ell$. We have $S(n, k)=a_{n-1}+S(n-1, k-1)$, so $$ k\\left(M_{n}-a_{n-1}\\right)=S(n, k)-k a_{n-1}=S(n-1, k-1)-(k-1) a_{n-1} \\leqslant(k-1)\\left(M_{n-1}-a_{n-1}\\right), $$ since $S(n-1, k-1) \\leqslant(k-1) M_{n-1}$. Similarly, we get $$ \\ell\\left(a_{n-1}-m_{n}\\right)=(\\ell-1) a_{n-1}-S(n-1, \\ell-1) \\leqslant(\\ell-1)\\left(a_{n-1}-m_{n-1}\\right) . $$ Since $m_{n-1} \\leqslant a_{n-1} \\leqslant M_{n-1}$ and $k, \\ell \\leqslant n$, the obtained inequalities yield $$ \\begin{array}{ll} M_{n}-a_{n-1} \\leqslant \\frac{k-1}{k}\\left(M_{n-1}-a_{n-1}\\right) \\leqslant \\frac{n-1}{n}\\left(M_{n-1}-a_{n-1}\\right) \\quad \\text { and } \\\\ a_{n-1}-m_{n} \\leqslant \\frac{\\ell-1}{\\ell}\\left(a_{n-1}-m_{n-1}\\right) \\leqslant \\frac{n-1}{n}\\left(a_{n-1}-m_{n-1}\\right) . \\end{array} $$ Therefore, $$ \\Delta_{n}=\\left(M_{n}-a_{n-1}\\right)+\\left(a_{n-1}-m_{n}\\right) \\leqslant \\frac{n-1}{n}\\left(\\left(M_{n-1}-a_{n-1}\\right)+\\left(a_{n-1}-m_{n-1}\\right)\\right)=\\frac{n-1}{n} \\Delta_{n-1} . $$ Back to the problem, if $a_{n}=1$ for all $n \\leqslant 2017$, then $a_{2018} \\leqslant 1$ and hence $a_{2018}-a_{2017} \\leqslant 0$. Otherwise, let $2 \\leqslant q \\leqslant 2017$ be the minimal index with $a_{q}<1$. We have $S(q, i)=i$ for all $i=1,2, \\ldots, q-1$, while $S(q, q)=q-1$. Therefore, $a_{q}<1$ yields $a_{q}=S(q, q) / q=1-\\frac{1}{q}$. Now we have $S(q+1, i)=i-\\frac{1}{q}$ for $i=1,2, \\ldots, q$, and $S(q+1, q+1)=q-\\frac{1}{q}$. This gives us $$ m_{q+1}=\\frac{S(q+1,1)}{1}=\\frac{S(q+1, q+1)}{q+1}=\\frac{q-1}{q} \\quad \\text { and } \\quad M_{q+1}=\\frac{S(q+1, q)}{q}=\\frac{q^{2}-1}{q^{2}} $$ so $\\Delta_{q+1}=M_{q+1}-m_{q+1}=(q-1) / q^{2}$. Denoting $N=2017 \\geqslant q$ and using Claim 1 for $n=q+2, q+3, \\ldots, N+1$ we finally obtain $$ \\Delta_{N+1} \\leqslant \\frac{q-1}{q^{2}} \\cdot \\frac{q+1}{q+2} \\cdot \\frac{q+2}{q+3} \\cdots \\frac{N}{N+1}=\\frac{1}{N+1}\\left(1-\\frac{1}{q^{2}}\\right) \\leqslant \\frac{1}{N+1}\\left(1-\\frac{1}{N^{2}}\\right)=\\frac{N-1}{N^{2}} $$ as required. Comment 1. One may check that the maximal value of $a_{2018}-a_{2017}$ is attained at the unique sequence, which is presented in the solution above. Comment 2. An easier question would be to determine the maximal value of $\\left|a_{2018}-a_{2017}\\right|$. In this version, the answer $\\frac{1}{2018}$ is achieved at $$ a_{1}=a_{2}=\\cdots=a_{2017}=1, \\quad a_{2018}=\\frac{a_{2017}+\\cdots+a_{0}}{2018}=1-\\frac{1}{2018} . $$ To prove that this value is optimal, it suffices to notice that $\\Delta_{2}=\\frac{1}{2}$ and to apply Claim 1 obtaining $$ \\left|a_{2018}-a_{2017}\\right| \\leqslant \\Delta_{2018} \\leqslant \\frac{1}{2} \\cdot \\frac{2}{3} \\cdots \\frac{2017}{2018}=\\frac{1}{2018} . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A4", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Let $a_{0}, a_{1}, a_{2}, \\ldots$ be a sequence of real numbers such that $a_{0}=0, a_{1}=1$, and for every $n \\geqslant 2$ there exists $1 \\leqslant k \\leqslant n$ satisfying $$ a_{n}=\\frac{a_{n-1}+\\cdots+a_{n-k}}{k} $$ Find the maximal possible value of $a_{2018}-a_{2017}$. (Belgium) Answer: The maximal value is $\\frac{2016}{2017^{2}}$.", "solution": "We present a different proof of the estimate $a_{2018}-a_{2017} \\leqslant \\frac{2016}{2017^{2}}$. We keep the same notations of $S(n, k), m_{n}$ and $M_{n}$ from the previous solution. Notice that $S(n, n)=S(n, n-1)$, as $a_{0}=0$. Also notice that for $0 \\leqslant k \\leqslant \\ell \\leqslant n$ we have $S(n, \\ell)=S(n, k)+S(n-k, \\ell-k)$. Claim 2. For every positive integer $n$, we have $m_{n} \\leqslant m_{n+1}$ and $M_{n+1} \\leqslant M_{n}$, so the segment $\\left[m_{n+1}, M_{n+1}\\right]$ is contained in $\\left[m_{n}, M_{n}\\right]$. Proof. Choose a positive integer $k \\leqslant n+1$ such that $m_{n+1}=S(n+1, k) / k$. Then we have $$ k m_{n+1}=S(n+1, k)=a_{n}+S(n, k-1) \\geqslant m_{n}+(k-1) m_{n}=k m_{n}, $$ which establishes the first inequality in the Claim. The proof of the second inequality is similar. Claim 3. For every positive integers $k \\geqslant n$, we have $m_{n} \\leqslant a_{k} \\leqslant M_{n}$. Proof. By Claim 2, we have $\\left[m_{k}, M_{k}\\right] \\subseteq\\left[m_{k-1}, M_{k-1}\\right] \\subseteq \\cdots \\subseteq\\left[m_{n}, M_{n}\\right]$. Since $a_{k} \\in\\left[m_{k}, M_{k}\\right]$, the claim follows. Claim 4. For every integer $n \\geqslant 2$, we have $M_{n}=S(n, n-1) /(n-1)$ and $m_{n}=S(n, n) / n$. Proof. We use induction on $n$. The base case $n=2$ is routine. To perform the induction step, we need to prove the inequalities $$ \\frac{S(n, n)}{n} \\leqslant \\frac{S(n, k)}{k} \\quad \\text { and } \\quad \\frac{S(n, k)}{k} \\leqslant \\frac{S(n, n-1)}{n-1} $$ for every positive integer $k \\leqslant n$. Clearly, these inequalities hold for $k=n$ and $k=n-1$, as $S(n, n)=S(n, n-1)>0$. In the sequel, we assume that $k<n-1$. Now the first inequality in (1) rewrites as $n S(n, k) \\geqslant k S(n, n)=k(S(n, k)+S(n-k, n-k))$, or, cancelling the terms occurring on both parts, as $$ (n-k) S(n, k) \\geqslant k S(n-k, n-k) \\Longleftrightarrow S(n, k) \\geqslant k \\cdot \\frac{S(n-k, n-k)}{n-k} $$ By the induction hypothesis, we have $S(n-k, n-k) /(n-k)=m_{n-k}$. By Claim 3, we get $a_{n-i} \\geqslant m_{n-k}$ for all $i=1,2, \\ldots, k$. Summing these $k$ inequalities we obtain $$ S(n, k) \\geqslant k m_{n-k}=k \\cdot \\frac{S(n-k, n-k)}{n-k} $$ as required. The second inequality in (1) is proved similarly. Indeed, this inequality is equivalent to $$ \\begin{aligned} (n-1) S(n, k) \\leqslant k S(n, n-1) & \\Longleftrightarrow(n-k-1) S(n, k) \\leqslant k S(n-k, n-k-1) \\\\ & \\Longleftrightarrow S(n, k) \\leqslant k \\cdot \\frac{S(n-k, n-k-1)}{n-k-1}=k M_{n-k} ; \\end{aligned} $$ the last inequality follows again from Claim 3, as each term in $S(n, k)$ is at most $M_{n-k}$. Now we can prove the required estimate for $a_{2018}-a_{2017}$. Set $N=2017$. By Claim 4 , $$ \\begin{aligned} a_{N+1}-a_{N} \\leqslant M_{N+1}-a_{N}=\\frac{S(N+1, N)}{N}-a_{N} & =\\frac{a_{N}+S(N, N-1)}{N}-a_{N} \\\\ & =\\frac{S(N, N-1)}{N}-\\frac{N-1}{N} \\cdot a_{N} . \\end{aligned} $$ On the other hand, the same Claim yields $$ a_{N} \\geqslant m_{N}=\\frac{S(N, N)}{N}=\\frac{S(N, N-1)}{N} . $$ Noticing that each term in $S(N, N-1)$ is at most 1 , so $S(N, N-1) \\leqslant N-1$, we finally obtain $$ a_{N+1}-a_{N} \\leqslant \\frac{S(N, N-1)}{N}-\\frac{N-1}{N} \\cdot \\frac{S(N, N-1)}{N}=\\frac{S(N, N-1)}{N^{2}} \\leqslant \\frac{N-1}{N^{2}} . $$ Comment 1. Claim 1 in Solution 1 can be deduced from Claims 2 and 4 in Solution 2. By Claim 4 we have $M_{n}=\\frac{S(n, n-1)}{n-1}$ and $m_{n}=\\frac{S(n, n)}{n}=\\frac{S(n, n-1)}{n}$. It follows that $\\Delta_{n}=M_{n}-m_{n}=$ $\\frac{S(n, n-1)}{(n-1) n}$ and so $M_{n}=n \\Delta_{n}$ and $m_{n}=(n-1) \\Delta_{n}$ Similarly, $M_{n-1}=(n-1) \\Delta_{n-1}$ and $m_{n-1}=(n-2) \\Delta_{n-1}$. Then the inequalities $m_{n-1} \\leqslant m_{n}$ and $M_{n} \\leqslant M_{n-1}$ from Claim 2 write as $(n-2) \\Delta_{n-1} \\leqslant(n-1) \\Delta_{n}$ and $n \\Delta_{n} \\leqslant(n-1) \\Delta_{n-1}$. Hence we have the double inequality $$ \\frac{n-2}{n-1} \\Delta_{n-1} \\leqslant \\Delta_{n} \\leqslant \\frac{n-1}{n} \\Delta_{n-1} $$ Comment 2. Both solutions above discuss the properties of an arbitrary sequence satisfying the problem conditions. Instead, one may investigate only an optimal sequence which maximises the value of $a_{2018}-a_{2017}$. Here we present an observation which allows to simplify such investigation - for instance, the proofs of Claim 1 in Solution 1 and Claim 4 in Solution 2. The sequence $\\left(a_{n}\\right)$ is uniquely determined by choosing, for every $n \\geqslant 2$, a positive integer $k(n) \\leqslant n$ such that $a_{n}=S(n, k(n)) / k(n)$. Take an arbitrary $2 \\leqslant n_{0} \\leqslant 2018$, and assume that all such integers $k(n)$, for $n \\neq n_{0}$, are fixed. Then, for every $n$, the value of $a_{n}$ is a linear function in $a_{n_{0}}$ (whose possible values constitute some discrete subset of $\\left[m_{n_{0}}, M_{n_{0}}\\right]$ containing both endpoints). Hence, $a_{2018}-a_{2017}$ is also a linear function in $a_{n_{0}}$, so it attains its maximal value at one of the endpoints of the segment $\\left[m_{n_{0}}, M_{n_{0}}\\right]$. This shows that, while dealing with an optimal sequence, we may assume $a_{n} \\in\\left\\{m_{n}, M_{n}\\right\\}$ for all $2 \\leqslant n \\leqslant 2018$. Now one can easily see that, if $a_{n}=m_{n}$, then $m_{n+1}=m_{n}$ and $M_{n+1} \\leqslant \\frac{m_{n}+n M_{n}}{n+1} ;$ similar estimates hold in the case $a_{n}=M_{n}$. This already establishes Claim 1, and simplifies the inductive proof of Claim 4, both applied to an optimal sequence.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A5", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Determine all functions $f:(0, \\infty) \\rightarrow \\mathbb{R}$ satisfying $$ \\left(x+\\frac{1}{x}\\right) f(y)=f(x y)+f\\left(\\frac{y}{x}\\right) $$ for all $x, y>0$. (South Korea) Answer: $f(x)=C_{1} x+\\frac{C_{2}}{x}$ with arbitrary constants $C_{1}$ and $C_{2}$.", "solution": "Fix a real number $a>1$, and take a new variable $t$. For the values $f(t), f\\left(t^{2}\\right)$, $f(a t)$ and $f\\left(a^{2} t^{2}\\right)$, the relation (1) provides a system of linear equations: $$ \\begin{array}{llll} x=y=t: & \\left(t+\\frac{1}{t}\\right) f(t) & =f\\left(t^{2}\\right)+f(1) \\\\ x=\\frac{t}{a}, y=a t: & \\left(\\frac{t}{a}+\\frac{a}{t}\\right) f(a t) & =f\\left(t^{2}\\right)+f\\left(a^{2}\\right) \\\\ x=a^{2} t, y=t: & \\left(a^{2} t+\\frac{1}{a^{2} t}\\right) f(t) & =f\\left(a^{2} t^{2}\\right)+f\\left(\\frac{1}{a^{2}}\\right) \\\\ x=y=a t: & \\left(a t+\\frac{1}{a t}\\right) f(a t) & =f\\left(a^{2} t^{2}\\right)+f(1) \\end{array} $$ In order to eliminate $f\\left(t^{2}\\right)$, take the difference of (2a) and (2b); from (2c) and (2d) eliminate $f\\left(a^{2} t^{2}\\right)$; then by taking a linear combination, eliminate $f(a t)$ as well: $$ \\begin{gathered} \\left(t+\\frac{1}{t}\\right) f(t)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right) f(a t)=f(1)-f\\left(a^{2}\\right) \\text { and } \\\\ \\left(a^{2} t+\\frac{1}{a^{2} t}\\right) f(t)-\\left(a t+\\frac{1}{a t}\\right) f(a t)=f\\left(1 / a^{2}\\right)-f(1), \\text { so } \\\\ \\left(\\left(a t+\\frac{1}{a t}\\right)\\left(t+\\frac{1}{t}\\right)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right)\\left(a^{2} t+\\frac{1}{a^{2} t}\\right)\\right) f(t) \\\\ =\\left(a t+\\frac{1}{a t}\\right)\\left(f(1)-f\\left(a^{2}\\right)\\right)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right)\\left(f\\left(1 / a^{2}\\right)-f(1)\\right) . \\end{gathered} $$ Notice that on the left-hand side, the coefficient of $f(t)$ is nonzero and does not depend on $t$ : $$ \\left(a t+\\frac{1}{a t}\\right)\\left(t+\\frac{1}{t}\\right)-\\left(\\frac{t}{a}+\\frac{a}{t}\\right)\\left(a^{2} t+\\frac{1}{a^{2} t}\\right)=a+\\frac{1}{a}-\\left(a^{3}+\\frac{1}{a^{3}}\\right)<0 . $$ After dividing by this fixed number, we get $$ f(t)=C_{1} t+\\frac{C_{2}}{t} $$ where the numbers $C_{1}$ and $C_{2}$ are expressed in terms of $a, f(1), f\\left(a^{2}\\right)$ and $f\\left(1 / a^{2}\\right)$, and they do not depend on $t$. The functions of the form (3) satisfy the equation: $$ \\left(x+\\frac{1}{x}\\right) f(y)=\\left(x+\\frac{1}{x}\\right)\\left(C_{1} y+\\frac{C_{2}}{y}\\right)=\\left(C_{1} x y+\\frac{C_{2}}{x y}\\right)+\\left(C_{1} \\frac{y}{x}+C_{2} \\frac{x}{y}\\right)=f(x y)+f\\left(\\frac{y}{x}\\right) . $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A5", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Determine all functions $f:(0, \\infty) \\rightarrow \\mathbb{R}$ satisfying $$ \\left(x+\\frac{1}{x}\\right) f(y)=f(x y)+f\\left(\\frac{y}{x}\\right) $$ for all $x, y>0$. (South Korea) Answer: $f(x)=C_{1} x+\\frac{C_{2}}{x}$ with arbitrary constants $C_{1}$ and $C_{2}$.", "solution": "We start with an observation. If we substitute $x=a \\neq 1$ and $y=a^{n}$ in (1), we obtain $$ f\\left(a^{n+1}\\right)-\\left(a+\\frac{1}{a}\\right) f\\left(a^{n}\\right)+f\\left(a^{n-1}\\right)=0 . $$ For the sequence $z_{n}=a^{n}$, this is a homogeneous linear recurrence of the second order, and its characteristic polynomial is $t^{2}-\\left(a+\\frac{1}{a}\\right) t+1=(t-a)\\left(t-\\frac{1}{a}\\right)$ with two distinct nonzero roots, namely $a$ and $1 / a$. As is well-known, the general solution is $z_{n}=C_{1} a^{n}+C_{2}(1 / a)^{n}$ where the index $n$ can be as well positive as negative. Of course, the numbers $C_{1}$ and $C_{2}$ may depend of the choice of $a$, so in fact we have two functions, $C_{1}$ and $C_{2}$, such that $$ f\\left(a^{n}\\right)=C_{1}(a) \\cdot a^{n}+\\frac{C_{2}(a)}{a^{n}} \\quad \\text { for every } a \\neq 1 \\text { and every integer } n \\text {. } $$ The relation (4) can be easily extended to rational values of $n$, so we may conjecture that $C_{1}$ and $C_{2}$ are constants, and whence $f(t)=C_{1} t+\\frac{C_{2}}{t}$. As it was seen in the previous solution, such functions indeed satisfy (1). The equation (1) is linear in $f$; so if some functions $f_{1}$ and $f_{2}$ satisfy (1) and $c_{1}, c_{2}$ are real numbers, then $c_{1} f_{1}(x)+c_{2} f_{2}(x)$ is also a solution of (1). In order to make our formulas simpler, define $$ f_{0}(x)=f(x)-f(1) \\cdot x \\text {. } $$ This function is another one satisfying (1) and the extra constraint $f_{0}(1)=0$. Repeating the same argument on linear recurrences, we can write $f_{0}(a)=K(a) a^{n}+\\frac{L(a)}{a^{n}}$ with some functions $K$ and $L$. By substituting $n=0$, we can see that $K(a)+L(a)=f_{0}(1)=0$ for every $a$. Hence, $$ f_{0}\\left(a^{n}\\right)=K(a)\\left(a^{n}-\\frac{1}{a^{n}}\\right) $$ Now take two numbers $a>b>1$ arbitrarily and substitute $x=(a / b)^{n}$ and $y=(a b)^{n}$ in (1): $$ \\begin{aligned} \\left(\\frac{a^{n}}{b^{n}}+\\frac{b^{n}}{a^{n}}\\right) f_{0}\\left((a b)^{n}\\right) & =f_{0}\\left(a^{2 n}\\right)+f_{0}\\left(b^{2 n}\\right), \\quad \\text { so } \\\\ \\left(\\frac{a^{n}}{b^{n}}+\\frac{b^{n}}{a^{n}}\\right) K(a b)\\left((a b)^{n}-\\frac{1}{(a b)^{n}}\\right) & =K(a)\\left(a^{2 n}-\\frac{1}{a^{2 n}}\\right)+K(b)\\left(b^{2 n}-\\frac{1}{b^{2 n}}\\right), \\quad \\text { or equivalently } \\\\ K(a b)\\left(a^{2 n}-\\frac{1}{a^{2 n}}+b^{2 n}-\\frac{1}{b^{2 n}}\\right) & =K(a)\\left(a^{2 n}-\\frac{1}{a^{2 n}}\\right)+K(b)\\left(b^{2 n}-\\frac{1}{b^{2 n}}\\right) . \\end{aligned} $$ By dividing (5) by $a^{2 n}$ and then taking limit with $n \\rightarrow+\\infty$ we get $K(a b)=K(a)$. Then (5) reduces to $K(a)=K(b)$. Hence, $K(a)=K(b)$ for all $a>b>1$. Fix $a>1$. For every $x>0$ there is some $b$ and an integer $n$ such that $1<b<a$ and $x=b^{n}$. Then $$ f_{0}(x)=f_{0}\\left(b^{n}\\right)=K(b)\\left(b^{n}-\\frac{1}{b^{n}}\\right)=K(a)\\left(x-\\frac{1}{x}\\right) . $$ Hence, we have $f(x)=f_{0}(x)+f(1) x=C_{1} x+\\frac{C_{2}}{x}$ with $C_{1}=K(a)+f(1)$ and $C_{2}=-K(a)$. Comment. After establishing (5), there are several variants of finishing the solution. For example, instead of taking a limit, we can obtain a system of linear equations for $K(a), K(b)$ and $K(a b)$ by substituting two positive integers $n$ in (5), say $n=1$ and $n=2$. This approach leads to a similar ending as in the first solution. Optionally, we define another function $f_{1}(x)=f_{0}(x)-C\\left(x-\\frac{1}{x}\\right)$ and prescribe $K(c)=0$ for another fixed $c$. Then we can choose $a b=c$ and decrease the number of terms in (5).", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A7", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find the maximal value of $$ S=\\sqrt[3]{\\frac{a}{b+7}}+\\sqrt[3]{\\frac{b}{c+7}}+\\sqrt[3]{\\frac{c}{d+7}}+\\sqrt[3]{\\frac{d}{a+7}} $$ where $a, b, c, d$ are nonnegative real numbers which satisfy $a+b+c+d=100$. (Taiwan) Answer: $\\frac{8}{\\sqrt[3]{7}}$, reached when $(a, b, c, d)$ is a cyclic permutation of $(1,49,1,49)$.", "solution": "Since the value $8 / \\sqrt[3]{7}$ is reached, it suffices to prove that $S \\leqslant 8 / \\sqrt[3]{7}$. Assume that $x, y, z, t$ is a permutation of the variables, with $x \\leqslant y \\leqslant z \\leqslant t$. Then, by the rearrangement inequality, $$ S \\leqslant\\left(\\sqrt[3]{\\frac{x}{t+7}}+\\sqrt[3]{\\frac{t}{x+7}}\\right)+\\left(\\sqrt[3]{\\frac{y}{z+7}}+\\sqrt[3]{\\frac{z}{y+7}}\\right) $$ Claim. The first bracket above does not exceed $\\sqrt[3]{\\frac{x+t+14}{7}}$. Proof. Since $$ X^{3}+Y^{3}+3 X Y Z-Z^{3}=\\frac{1}{2}(X+Y-Z)\\left((X-Y)^{2}+(X+Z)^{2}+(Y+Z)^{2}\\right) $$ the inequality $X+Y \\leqslant Z$ is equivalent (when $X, Y, Z \\geqslant 0$ ) to $X^{3}+Y^{3}+3 X Y Z \\leqslant Z^{3}$. Therefore, the claim is equivalent to $$ \\frac{x}{t+7}+\\frac{t}{x+7}+3 \\sqrt[3]{\\frac{x t(x+t+14)}{7(x+7)(t+7)}} \\leqslant \\frac{x+t+14}{7} $$ Notice that $$ \\begin{array}{r} 3 \\sqrt[3]{\\frac{x t(x+t+14)}{7(x+7)(t+7)}}=3 \\sqrt[3]{\\frac{t(x+7)}{7(t+7)} \\cdot \\frac{x(t+7)}{7(x+7)} \\cdot \\frac{7(x+t+14)}{(t+7)(x+7)}} \\\\ \\leqslant \\frac{t(x+7)}{7(t+7)}+\\frac{x(t+7)}{7(x+7)}+\\frac{7(x+t+14)}{(t+7)(x+7)} \\end{array} $$ by the AM-GM inequality, so it suffices to prove $$ \\frac{x}{t+7}+\\frac{t}{x+7}+\\frac{t(x+7)}{7(t+7)}+\\frac{x(t+7)}{7(x+7)}+\\frac{7(x+t+14)}{(t+7)(x+7)} \\leqslant \\frac{x+t+14}{7} . $$ A straightforward check verifies that the last inequality is in fact an equality. The claim leads now to $$ S \\leqslant \\sqrt[3]{\\frac{x+t+14}{7}}+\\sqrt[3]{\\frac{y+z+14}{7}} \\leqslant 2 \\sqrt[3]{\\frac{x+y+z+t+28}{14}}=\\frac{8}{\\sqrt[3]{7}} $$ the last inequality being due to the AM-CM inequality (or to the fact that $\\sqrt[3]{ }$ is concave on $[0, \\infty))$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "A7", "problem_type": "Algebra", "exam": "IMO-SL", "problem": "Find the maximal value of $$ S=\\sqrt[3]{\\frac{a}{b+7}}+\\sqrt[3]{\\frac{b}{c+7}}+\\sqrt[3]{\\frac{c}{d+7}}+\\sqrt[3]{\\frac{d}{a+7}} $$ where $a, b, c, d$ are nonnegative real numbers which satisfy $a+b+c+d=100$. (Taiwan) Answer: $\\frac{8}{\\sqrt[3]{7}}$, reached when $(a, b, c, d)$ is a cyclic permutation of $(1,49,1,49)$.", "solution": "We present a different proof for the estimate $S \\leqslant 8 / \\sqrt[3]{7}$. Start by using Hölder's inequality: $$ S^{3}=\\left(\\sum_{\\mathrm{cyc}} \\frac{\\sqrt[6]{a} \\cdot \\sqrt[6]{a}}{\\sqrt[3]{b+7}}\\right)^{3} \\leqslant \\sum_{\\mathrm{cyc}}(\\sqrt[6]{a})^{3} \\cdot \\sum_{\\mathrm{cyc}}(\\sqrt[6]{a})^{3} \\cdot \\sum_{\\mathrm{cyc}}\\left(\\frac{1}{\\sqrt[3]{b+7}}\\right)^{3}=\\left(\\sum_{\\mathrm{cyc}} \\sqrt{a}\\right)^{2} \\sum_{\\mathrm{cyc}} \\frac{1}{b+7} $$ Notice that $$ \\frac{(x-1)^{2}(x-7)^{2}}{x^{2}+7} \\geqslant 0 \\Longleftrightarrow x^{2}-16 x+71 \\geqslant \\frac{448}{x^{2}+7} $$ yields $$ \\sum \\frac{1}{b+7} \\leqslant \\frac{1}{448} \\sum(b-16 \\sqrt{b}+71)=\\frac{1}{448}\\left(384-16 \\sum \\sqrt{b}\\right)=\\frac{48-2 \\sum \\sqrt{b}}{56} $$ Finally, $$ S^{3} \\leqslant \\frac{1}{56}\\left(\\sum \\sqrt{a}\\right)^{2}\\left(48-2 \\sum \\sqrt{a}\\right) \\leqslant \\frac{1}{56}\\left(\\frac{\\sum \\sqrt{a}+\\sum \\sqrt{a}+\\left(48-2 \\sum \\sqrt{a}\\right)}{3}\\right)^{3}=\\frac{512}{7} $$ by the AM-GM inequality. The conclusion follows. Comment. All the above works if we replace 7 and 100 with $k>0$ and $2\\left(k^{2}+1\\right)$, respectively; in this case, the answer becomes $$ 2 \\sqrt[3]{\\frac{(k+1)^{2}}{k}} $$ Even further, a linear substitution allows to extend the solutions to a version with 7 and 100 being replaced with arbitrary positive real numbers $p$ and $q$ satisfying $q \\geqslant 4 p$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C2", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Queenie and Horst play a game on a $20 \\times 20$ chessboard. In the beginning the board is empty. In every turn, Horst places a black knight on an empty square in such a way that his new knight does not attack any previous knights. Then Queenie places a white queen on an empty square. The game gets finished when somebody cannot move. Find the maximal positive $K$ such that, regardless of the strategy of Queenie, Horst can put at least $K$ knights on the board. (Armenia) Answer: $K=20^{2} / 4=100$. In case of a $4 N \\times 4 M$ board, the answer is $K=4 N M$.", "solution": "We show two strategies, one for Horst to place at least 100 knights, and another strategy for Queenie that prevents Horst from putting more than 100 knights on the board. A strategy for Horst: Put knights only on black squares, until all black squares get occupied. Colour the squares of the board black and white in the usual way, such that the white and black squares alternate, and let Horst put his knights on black squares as long as it is possible. Two knights on squares of the same colour never attack each other. The number of black squares is $20^{2} / 2=200$. The two players occupy the squares in turn, so Horst will surely find empty black squares in his first 100 steps. A strategy for Queenie: Group the squares into cycles of length 4, and after each step of Horst, occupy the opposite square in the same cycle. Consider the squares of the board as vertices of a graph; let two squares be connected if two knights on those squares would attack each other. Notice that in a $4 \\times 4$ board the squares can be grouped into 4 cycles of length 4 , as shown in Figure 1. Divide the board into parts of size $4 \\times 4$, and perform the same grouping in every part; this way we arrange the 400 squares of the board into 100 cycles (Figure 2).  Figure 1  Figure 2  Figure 3 The strategy of Queenie can be as follows: Whenever Horst puts a new knight to a certain square $A$, which is part of some cycle $A-B-C-D-A$, let Queenie put her queen on the opposite square $C$ in that cycle (Figure 3). From this point, Horst cannot put any knight on $A$ or $C$ because those squares are already occupied, neither on $B$ or $D$ because those squares are attacked by the knight standing on $A$. Hence, Horst can put at most one knight on each cycle, that is at most 100 knights in total. Comment 1. Queenie's strategy can be prescribed by a simple rule: divide the board into $4 \\times 4$ parts; whenever Horst puts a knight in a part $P$, Queenie reflects that square about the centre of $P$ and puts her queen on the reflected square. Comment 2. The result remains the same if Queenie moves first. In the first turn, she may put her first queen arbitrarily. Later, if she has to put her next queen on a square that already contains a queen, she may move arbitrarily again.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C4", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "An anti-Pascal pyramid is a finite set of numbers, placed in a triangle-shaped array so that the first row of the array contains one number, the second row contains two numbers, the third row contains three numbers and so on; and, except for the numbers in the bottom row, each number equals the absolute value of the difference of the two numbers below it. For instance, the triangle below is an anti-Pascal pyramid with four rows, in which every integer from 1 to $1+2+3+4=10$ occurs exactly once: $$ \\begin{array}{ccccc} & & & \\\\ & 2 & 6 & \\\\ & 5 & 7 & \\\\ 8 & 3 & 10 & 9 . \\end{array} $$ Is it possible to form an anti-Pascal pyramid with 2018 rows, using every integer from 1 to $1+2+\\cdots+2018$ exactly once? (Iran) Answer: No, it is not possible.", "solution": "Let $T$ be an anti-Pascal pyramid with $n$ rows, containing every integer from 1 to $1+2+\\cdots+n$, and let $a_{1}$ be the topmost number in $T$ (Figure 1). The two numbers below $a_{1}$ are some $a_{2}$ and $b_{2}=a_{1}+a_{2}$, the two numbers below $b_{2}$ are some $a_{3}$ and $b_{3}=a_{1}+a_{2}+a_{3}$, and so on and so forth all the way down to the bottom row, where some $a_{n}$ and $b_{n}=a_{1}+a_{2}+\\cdots+a_{n}$ are the two neighbours below $b_{n-1}=a_{1}+a_{2}+\\cdots+a_{n-1}$. Since the $a_{k}$ are $n$ pairwise distinct positive integers whose sum does not exceed the largest number in $T$, which is $1+2+\\cdots+n$, it follows that they form a permutation of $1,2, \\ldots, n$.  Figure 1  Figure 2 Consider now (Figure 2) the two 'equilateral' subtriangles of $T$ whose bottom rows contain the numbers to the left, respectively right, of the pair $a_{n}, b_{n}$. (One of these subtriangles may very well be empty.) At least one of these subtriangles, say $T^{\\prime}$, has side length $\\ell \\geqslant\\lceil(n-2) / 2\\rceil$. Since $T^{\\prime}$ obeys the anti-Pascal rule, it contains $\\ell$ pairwise distinct positive integers $a_{1}^{\\prime}, a_{2}^{\\prime}, \\ldots, a_{\\ell}^{\\prime}$, where $a_{1}^{\\prime}$ is at the apex, and $a_{k}^{\\prime}$ and $b_{k}^{\\prime}=a_{1}^{\\prime}+a_{2}^{\\prime}+\\cdots+a_{k}^{\\prime}$ are the two neighbours below $b_{k-1}^{\\prime}$ for each $k=2,3 \\ldots, \\ell$. Since the $a_{k}$ all lie outside $T^{\\prime}$, and they form a permutation of $1,2, \\ldots, n$, the $a_{k}^{\\prime}$ are all greater than $n$. Consequently, $$ \\begin{array}{r} b_{\\ell}^{\\prime} \\geqslant(n+1)+(n+2)+\\cdots+(n+\\ell)=\\frac{\\ell(2 n+\\ell+1)}{2} \\\\ \\geqslant \\frac{1}{2} \\cdot \\frac{n-2}{2}\\left(2 n+\\frac{n-2}{2}+1\\right)=\\frac{5 n(n-2)}{8}, \\end{array} $$ which is greater than $1+2+\\cdots+n=n(n+1) / 2$ for $n=2018$. A contradiction. Comment. The above estimate may be slightly improved by noticing that $b_{\\ell}^{\\prime} \\neq b_{n}$. This implies $n(n+1) / 2=b_{n}>b_{\\ell}^{\\prime} \\geqslant\\lceil(n-2) / 2\\rceil(2 n+\\lceil(n-2) / 2\\rceil+1) / 2$, so $n \\leqslant 7$ if $n$ is odd, and $n \\leqslant 12$ if $n$ is even. It seems that the largest anti-Pascal pyramid whose entries are a permutation of the integers from 1 to $1+2+\\cdots+n$ has 5 rows.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $k$ be a positive integer. The organising committee of a tennis tournament is to schedule the matches for $2 k$ players so that every two players play once, each day exactly one match is played, and each player arrives to the tournament site the day of his first match, and departs the day of his last match. For every day a player is present on the tournament, the committee has to pay 1 coin to the hotel. The organisers want to design the schedule so as to minimise the total cost of all players' stays. Determine this minimum cost. (Russia) Answer: The required minimum is $k\\left(4 k^{2}+k-1\\right) / 2$.", "solution": "Enumerate the days of the tournament $1,2, \\ldots,\\left(\\begin{array}{c}2 k \\\\ 2\\end{array}\\right)$. Let $b_{1} \\leqslant b_{2} \\leqslant \\cdots \\leqslant b_{2 k}$ be the days the players arrive to the tournament, arranged in nondecreasing order; similarly, let $e_{1} \\geqslant \\cdots \\geqslant e_{2 k}$ be the days they depart arranged in nonincreasing order (it may happen that a player arrives on day $b_{i}$ and departs on day $e_{j}$, where $i \\neq j$ ). If a player arrives on day $b$ and departs on day $e$, then his stay cost is $e-b+1$. Therefore, the total stay cost is $$ \\Sigma=\\sum_{i=1}^{2 k} e_{i}-\\sum_{i=1}^{2 k} b_{i}+n=\\sum_{i=1}^{2 k}\\left(e_{i}-b_{i}+1\\right) $$ Bounding the total cost from below. To this end, estimate $e_{i+1}-b_{i+1}+1$. Before day $b_{i+1}$, only $i$ players were present, so at most $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ matches could be played. Therefore, $b_{i+1} \\leqslant\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)+1$. Similarly, at most $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ matches could be played after day $e_{i+1}$, so $e_{i} \\geqslant\\left(\\begin{array}{c}2 k \\\\ 2\\end{array}\\right)-\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$. Thus, $$ e_{i+1}-b_{i+1}+1 \\geqslant\\left(\\begin{array}{c} 2 k \\\\ 2 \\end{array}\\right)-2\\left(\\begin{array}{l} i \\\\ 2 \\end{array}\\right)=k(2 k-1)-i(i-1) $$ This lower bound can be improved for $i>k$ : List the $i$ players who arrived first, and the $i$ players who departed last; at least $2 i-2 k$ players appear in both lists. The matches between these players were counted twice, though the players in each pair have played only once. Therefore, if $i>k$, then $$ e_{i+1}-b_{i+1}+1 \\geqslant\\left(\\begin{array}{c} 2 k \\\\ 2 \\end{array}\\right)-2\\left(\\begin{array}{c} i \\\\ 2 \\end{array}\\right)+\\left(\\begin{array}{c} 2 i-2 k \\\\ 2 \\end{array}\\right)=(2 k-i)^{2} $$ An optimal tournament, We now describe a schedule in which the lower bounds above are all achieved simultaneously. Split players into two groups $X$ and $Y$, each of cardinality $k$. Next, partition the schedule into three parts. During the first part, the players from $X$ arrive one by one, and each newly arrived player immediately plays with everyone already present. During the third part (after all players from $X$ have already departed) the players from $Y$ depart one by one, each playing with everyone still present just before departing. In the middle part, everyone from $X$ should play with everyone from $Y$. Let $S_{1}, S_{2}, \\ldots, S_{k}$ be the players in $X$, and let $T_{1}, T_{2}, \\ldots, T_{k}$ be the players in $Y$. Let $T_{1}, T_{2}, \\ldots, T_{k}$ arrive in this order; after $T_{j}$ arrives, he immediately plays with all the $S_{i}, i>j$. Afterwards, players $S_{k}$, $S_{k-1}, \\ldots, S_{1}$ depart in this order; each $S_{i}$ plays with all the $T_{j}, i \\leqslant j$, just before his departure, and $S_{k}$ departs the day $T_{k}$ arrives. For $0 \\leqslant s \\leqslant k-1$, the number of matches played between $T_{k-s}$ 's arrival and $S_{k-s}$ 's departure is $$ \\sum_{j=k-s}^{k-1}(k-j)+1+\\sum_{j=k-s}^{k-1}(k-j+1)=\\frac{1}{2} s(s+1)+1+\\frac{1}{2} s(s+3)=(s+1)^{2} $$ Thus, if $i>k$, then the number of matches that have been played between $T_{i-k+1}$ 's arrival, which is $b_{i+1}$, and $S_{i-k+1}$ 's departure, which is $e_{i+1}$, is $(2 k-i)^{2}$; that is, $e_{i+1}-b_{i+1}+1=(2 k-i)^{2}$, showing the second lower bound achieved for all $i>k$. If $i \\leqslant k$, then the matches between the $i$ players present before $b_{i+1}$ all fall in the first part of the schedule, so there are $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ such, and $b_{i+1}=\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)+1$. Similarly, after $e_{i+1}$, there are $i$ players left, all $\\left(\\begin{array}{l}i \\\\ 2\\end{array}\\right)$ matches now fall in the third part of the schedule, and $e_{i+1}=\\left(\\begin{array}{c}2 k \\\\ 2\\end{array}\\right)-\\left(\\begin{array}{c}i \\\\ 2\\end{array}\\right)$. The first lower bound is therefore also achieved for all $i \\leqslant k$. Consequently, all lower bounds are achieved simultaneously, and the schedule is indeed optimal. Evaluation. Finally, evaluate the total cost for the optimal schedule: $$ \\begin{aligned} \\Sigma & =\\sum_{i=0}^{k}(k(2 k-1)-i(i-1))+\\sum_{i=k+1}^{2 k-1}(2 k-i)^{2}=(k+1) k(2 k-1)-\\sum_{i=0}^{k} i(i-1)+\\sum_{j=1}^{k-1} j^{2} \\\\ & =k(k+1)(2 k-1)-k^{2}+\\frac{1}{2} k(k+1)=\\frac{1}{2} k\\left(4 k^{2}+k-1\\right) . \\end{aligned} $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "C5", "problem_type": "Combinatorics", "exam": "IMO-SL", "problem": "Let $k$ be a positive integer. The organising committee of a tennis tournament is to schedule the matches for $2 k$ players so that every two players play once, each day exactly one match is played, and each player arrives to the tournament site the day of his first match, and departs the day of his last match. For every day a player is present on the tournament, the committee has to pay 1 coin to the hotel. The organisers want to design the schedule so as to minimise the total cost of all players' stays. Determine this minimum cost. (Russia) Answer: The required minimum is $k\\left(4 k^{2}+k-1\\right) / 2$.", "solution": "Consider any tournament schedule. Label players $P_{1}, P_{2}, \\ldots, P_{2 k}$ in order of their arrival, and label them again $Q_{2 k}, Q_{2 k-1}, \\ldots, Q_{1}$ in order of their departure, to define a permutation $a_{1}, a_{2}, \\ldots, a_{2 k}$ of $1,2, \\ldots, 2 k$ by $P_{i}=Q_{a_{i}}$. We first describe an optimal tournament for any given permutation $a_{1}, a_{2}, \\ldots, a_{2 k}$ of the indices $1,2, \\ldots, 2 k$. Next, we find an optimal permutation and an optimal tournament. Optimisation for a fixed $a_{1}, \\ldots, a_{2 k}$. We say that the cost of the match between $P_{i}$ and $P_{j}$ is the number of players present at the tournament when this match is played. Clearly, the Committee pays for each day the cost of the match of that day. Hence, we are to minimise the total cost of all matches. Notice that $Q_{2 k}$ 's departure does not precede $P_{2 k}$ 's arrival. Hence, the number of players at the tournament monotonically increases (non-strictly) until it reaches $2 k$, and then monotonically decreases (non-strictly). So, the best time to schedule the match between $P_{i}$ and $P_{j}$ is either when $P_{\\max (i, j)}$ arrives, or when $Q_{\\max \\left(a_{i}, a_{j}\\right)}$ departs, in which case the cost is $\\min \\left(\\max (i, j), \\max \\left(a_{i}, a_{j}\\right)\\right)$. Conversely, assuming that $i>j$, if this match is scheduled between the arrivals of $P_{i}$ and $P_{i+1}$, then its cost will be exactly $i=\\max (i, j)$. Similarly, one can make it cost $\\max \\left(a_{i}, a_{j}\\right)$. Obviously, these conditions can all be simultaneously satisfied, so the minimal cost for a fixed sequence $a_{1}, a_{2}, \\ldots, a_{2 k}$ is $$ \\Sigma\\left(a_{1}, \\ldots, a_{2 k}\\right)=\\sum_{1 \\leqslant i<j \\leqslant 2 k} \\min \\left(\\max (i, j), \\max \\left(a_{i}, a_{j}\\right)\\right) $$ Optimising the sequence $\\left(a_{i}\\right)$. Optimisation hinges on the lemma below. Lemma. If $a \\leqslant b$ and $c \\leqslant d$, then $$ \\begin{aligned} \\min (\\max (a, x), \\max (c, y))+\\min & (\\max (b, x), \\max (d, y)) \\\\ & \\geqslant \\min (\\max (a, x), \\max (d, y))+\\min (\\max (b, x), \\max (c, y)) \\end{aligned} $$ Proof. Write $a^{\\prime}=\\max (a, x) \\leqslant \\max (b, x)=b^{\\prime}$ and $c^{\\prime}=\\max (c, y) \\leqslant \\max (d, y)=d^{\\prime}$ and check that $\\min \\left(a^{\\prime}, c^{\\prime}\\right)+\\min \\left(b^{\\prime}, d^{\\prime}\\right) \\geqslant \\min \\left(a^{\\prime}, d^{\\prime}\\right)+\\min \\left(b^{\\prime}, c^{\\prime}\\right)$. Consider a permutation $a_{1}, a_{2}, \\ldots, a_{2 k}$ such that $a_{i}<a_{j}$ for some $i<j$. Swapping $a_{i}$ and $a_{j}$ does not change the $(i, j)$ th summand in (1), and for $\\ell \\notin\\{i, j\\}$ the sum of the $(i, \\ell)$ th and the $(j, \\ell)$ th summands does not increase by the Lemma. Hence the optimal value does not increase, but the number of disorders in the permutation increases. This process stops when $a_{i}=2 k+1-i$ for all $i$, so the required minimum is $$ \\begin{aligned} S(2 k, 2 k-1, \\ldots, 1) & =\\sum_{1 \\leqslant i<j \\leqslant 2 k} \\min (\\max (i, j), \\max (2 k+1-i, 2 k+1-j)) \\\\ & =\\sum_{1 \\leqslant i<j \\leqslant 2 k} \\min (j, 2 k+1-i) . \\end{aligned} $$ The latter sum is fairly tractable and yields the stated result; we omit the details. Comment. If the number of players is odd, say, $2 k-1$, the required minimum is $k(k-1)(4 k-1) / 2$. In this case, $|X|=k,|Y|=k-1$, the argument goes along the same lines, but some additional technicalities are to be taken care of. This page is intentionally left blank", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G3", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "A circle $\\omega$ of radius 1 is given. A collection $T$ of triangles is called good, if the following conditions hold: (i) each triangle from $T$ is inscribed in $\\omega$; (ii) no two triangles from $T$ have a common interior point. Determine all positive real numbers $t$ such that, for each positive integer $n$, there exists a good collection of $n$ triangles, each of perimeter greater than $t$. (South Africa) Answer: $t \\in(0,4]$.", "solution": "First, we show how to construct a good collection of $n$ triangles, each of perimeter greater than 4 . This will show that all $t \\leqslant 4$ satisfy the required conditions. Construct inductively an $(n+2)$-gon $B A_{1} A_{2} \\ldots A_{n} C$ inscribed in $\\omega$ such that $B C$ is a diameter, and $B A_{1} A_{2}, B A_{2} A_{3}, \\ldots, B A_{n-1} A_{n}, B A_{n} C$ is a good collection of $n$ triangles. For $n=1$, take any triangle $B A_{1} C$ inscribed in $\\omega$ such that $B C$ is a diameter; its perimeter is greater than $2 B C=4$. To perform the inductive step, assume that the $(n+2)$-gon $B A_{1} A_{2} \\ldots A_{n} C$ is already constructed. Since $A_{n} B+A_{n} C+B C>4$, one can choose a point $A_{n+1}$ on the small arc $\\widehat{C A_{n}}$, close enough to $C$, so that $A_{n} B+A_{n} A_{n+1}+B A_{n+1}$ is still greater than 4 . Thus each of these new triangles $B A_{n} A_{n+1}$ and $B A_{n+1} C$ has perimeter greater than 4, which completes the induction step.  We proceed by showing that no $t>4$ satisfies the conditions of the problem. To this end, we assume that there exists a good collection $T$ of $n$ triangles, each of perimeter greater than $t$, and then bound $n$ from above. Take $\\varepsilon>0$ such that $t=4+2 \\varepsilon$. Claim. There exists a positive constant $\\sigma=\\sigma(\\varepsilon)$ such that any triangle $\\Delta$ with perimeter $2 s \\geqslant 4+2 \\varepsilon$, inscribed in $\\omega$, has area $S(\\Delta)$ at least $\\sigma$. Proof. Let $a, b, c$ be the side lengths of $\\Delta$. Since $\\Delta$ is inscribed in $\\omega$, each side has length at most 2. Therefore, $s-a \\geqslant(2+\\varepsilon)-2=\\varepsilon$. Similarly, $s-b \\geqslant \\varepsilon$ and $s-c \\geqslant \\varepsilon$. By Heron's formula, $S(\\Delta)=\\sqrt{s(s-a)(s-b)(s-c)} \\geqslant \\sqrt{(2+\\varepsilon) \\varepsilon^{3}}$. Thus we can set $\\sigma(\\varepsilon)=\\sqrt{(2+\\varepsilon) \\varepsilon^{3}}$. Now we see that the total area $S$ of all triangles from $T$ is at least $n \\sigma(\\varepsilon)$. On the other hand, $S$ does not exceed the area of the disk bounded by $\\omega$. Thus $n \\sigma(\\varepsilon) \\leqslant \\pi$, which means that $n$ is bounded from above. Comment 1. One may prove the Claim using the formula $S=\\frac{a b c}{4 R}$ instead of Heron's formula. Comment 2. In the statement of the problem condition $(i)$ could be replaced by a weaker one: each triangle from $T$ lies within $\\omega$. This does not affect the solution above, but reduces the number of ways to prove the Claim. This page is intentionally left blank", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with circumcircle $\\omega$ and incentre $I$. A line $\\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\\Theta$. Show that the circumcircle of the triangle $\\Theta$ is tangent to $\\omega$. (Denmark) Preamble. Let $X=y \\cap z, Y=x \\cap z, Z=x \\cap y$ and let $\\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\\Delta$ and $\\delta$ inscribed into $\\Omega$ and $\\omega$, respectively. In order to prove that $\\Omega$ and $\\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\\Delta$ to $\\delta$ lies on $\\omega$ (or $\\Omega$ ), or, in other words, to show that $\\Delta$ and $\\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\\omega$ (or $\\Omega$ ). We use directed angles throughout all the solutions.", "solution": "Claim 1. The reflections $\\ell_{a}, \\ell_{b}$ and $\\ell_{c}$ of the line $\\ell$ in the lines $x, y$, and $z$, respectively, are concurrent at a point $T$ which belongs to $\\omega$.  Proof. Notice that $\\Varangle\\left(\\ell_{b}, \\ell_{c}\\right)=\\Varangle\\left(\\ell_{b}, \\ell\\right)+\\Varangle\\left(\\ell, \\ell_{c}\\right)=2 \\Varangle(y, \\ell)+2 \\Varangle(\\ell, z)=2 \\Varangle(y, z)$. But $y \\perp B I$ and $z \\perp C I$ implies $\\Varangle(y, z)=\\Varangle(B I, I C)$, so, since $2 \\Varangle(B I, I C)=\\Varangle(B A, A C)$, we obtain $$ \\Varangle\\left(\\ell_{b}, \\ell_{c}\\right)=\\Varangle(B A, A C) . $$ Since $A$ is the reflection of $D$ in $x$, $A$ belongs to $\\ell_{a}$; similarly, $B$ belongs to $\\ell_{b}$. Then (1) shows that the common point $T^{\\prime}$ of $\\ell_{a}$ and $\\ell_{b}$ lies on $\\omega$; similarly, the common point $T^{\\prime \\prime}$ of $\\ell_{c}$ and $\\ell_{b}$ lies on $\\omega$. If $B \\notin \\ell_{a}$ and $B \\notin \\ell_{c}$, then $T^{\\prime}$ and $T^{\\prime \\prime}$ are the second point of intersection of $\\ell_{b}$ and $\\omega$, hence they coincide. Otherwise, if, say, $B \\in \\ell_{c}$, then $\\ell_{c}=B C$, so $\\Varangle(B A, A C)=\\Varangle\\left(\\ell_{b}, \\ell_{c}\\right)=\\Varangle\\left(\\ell_{b}, B C\\right)$, which shows that $\\ell_{b}$ is tangent at $B$ to $\\omega$ and $T^{\\prime}=T^{\\prime \\prime}=B$. So $T^{\\prime}$ and $T^{\\prime \\prime}$ coincide in all the cases, and the conclusion of the claim follows. Now we prove that $X, X_{0}, T$ are collinear. Denote by $D_{b}$ and $D_{c}$ the reflections of the point $D$ in the lines $y$ and $z$, respectively. Then $D_{b}$ lies on $\\ell_{b}, D_{c}$ lies on $\\ell_{c}$, and $$ \\begin{aligned} \\Varangle\\left(D_{b} X, X D_{c}\\right) & =\\Varangle\\left(D_{b} X, D X\\right)+\\Varangle\\left(D X, X D_{c}\\right)=2 \\Varangle(y, D X)+2 \\Varangle(D X, z)=2 \\Varangle(y, z) \\\\ & =\\Varangle(B A, A C)=\\Varangle(B T, T C), \\end{aligned} $$ hence the quadrilateral $X D_{b} T D_{c}$ is cyclic. Notice also that since $X D_{b}=X D=X D_{c}$, the points $D, D_{b}, D_{c}$ lie on a circle with centre $X$. Using in this circle the diameter $D_{c} D_{c}^{\\prime}$ yields $\\Varangle\\left(D_{b} D_{c}, D_{c} X\\right)=90^{\\circ}+\\Varangle\\left(D_{b} D_{c}^{\\prime}, D_{c}^{\\prime} X\\right)=90^{\\circ}+\\Varangle\\left(D_{b} D, D D_{c}\\right)$. Therefore, $$ \\begin{gathered} \\Varangle\\left(\\ell_{b}, X T\\right)=\\Varangle\\left(D_{b} T, X T\\right)=\\Varangle\\left(D_{b} D_{c}, D_{c} X\\right)=90^{\\circ}+\\Varangle\\left(D_{b} D, D D_{c}\\right) \\\\ =90^{\\circ}+\\Varangle(B I, I C)=\\Varangle(B A, A I)=\\Varangle\\left(B A, A X_{0}\\right)=\\Varangle\\left(B T, T X_{0}\\right)=\\Varangle\\left(\\ell_{b}, X_{0} T\\right) \\end{gathered} $$ so the points $X, X_{0}, T$ are collinear. By a similar argument, $Y, Y_{0}, T$ and $Z, Z_{0}, T$ are collinear. As mentioned in the preamble, the statement of the problem follows. Comment 1. After proving Claim 1 one may proceed in another way. As it was shown, the reflections of $\\ell$ in the sidelines of $X Y Z$ are concurrent at $T$. Thus $\\ell$ is the Steiner line of $T$ with respect to $\\triangle X Y Z$ (that is the line containing the reflections $T_{a}, T_{b}, T_{c}$ of $T$ in the sidelines of $X Y Z$ ). The properties of the Steiner line imply that $T$ lies on $\\Omega$, and $\\ell$ passes through the orthocentre $H$ of the triangle $X Y Z$.  Let $H_{a}, H_{b}$, and $H_{c}$ be the reflections of the point $H$ in the lines $x, y$, and $z$, respectively. Then the triangle $H_{a} H_{b} H_{c}$ is inscribed in $\\Omega$ and homothetic to $A B C$ (by an easy angle chasing). Since $H_{a} \\in \\ell_{a}, H_{b} \\in \\ell_{b}$, and $H_{c} \\in \\ell_{c}$, the triangles $H_{a} H_{b} H_{c}$ and $A B C$ form a required pair of triangles $\\Delta$ and $\\delta$ mentioned in the preamble. Comment 2. The following observation shows how one may guess the description of the tangency point $T$ from Solution 1. Let us fix a direction and move the line $\\ell$ parallel to this direction with constant speed. Then the points $D, E$, and $F$ are moving with constant speeds along the lines $A I, B I$, and $C I$, respectively. In this case $x, y$, and $z$ are moving with constant speeds, defining a family of homothetic triangles $X Y Z$ with a common centre of homothety $T$. Notice that the triangle $X_{0} Y_{0} Z_{0}$ belongs to this family (for $\\ell$ passing through $I$ ). We may specify the location of $T$ considering the degenerate case when $x, y$, and $z$ are concurrent. In this degenerate case all the lines $x, y, z, \\ell, \\ell_{a}, \\ell_{b}, \\ell_{c}$ have a common point. Note that the lines $\\ell_{a}, \\ell_{b}, \\ell_{c}$ remain constant as $\\ell$ is moving (keeping its direction). Thus $T$ should be the common point of $\\ell_{a}, \\ell_{b}$, and $\\ell_{c}$, lying on $\\omega$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with circumcircle $\\omega$ and incentre $I$. A line $\\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\\Theta$. Show that the circumcircle of the triangle $\\Theta$ is tangent to $\\omega$. (Denmark) Preamble. Let $X=y \\cap z, Y=x \\cap z, Z=x \\cap y$ and let $\\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\\Delta$ and $\\delta$ inscribed into $\\Omega$ and $\\omega$, respectively. In order to prove that $\\Omega$ and $\\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\\Delta$ to $\\delta$ lies on $\\omega$ (or $\\Omega$ ), or, in other words, to show that $\\Delta$ and $\\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\\omega$ (or $\\Omega$ ). We use directed angles throughout all the solutions.", "solution": "As mentioned in the preamble, it is sufficient to prove that the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\\omega$. Thus, it suffices to prove that $\\Varangle\\left(T X_{0}, T Y_{0}\\right)=$ $\\Varangle\\left(Z_{0} X_{0}, Z_{0} Y_{0}\\right)$, or, equivalently, $\\Varangle\\left(X X_{0}, Y Y_{0}\\right)=\\Varangle\\left(Z_{0} X_{0}, Z_{0} Y_{0}\\right)$. Recall that $Y Z$ and $Y_{0} Z_{0}$ are the perpendicular bisectors of $A D$ and $A I$, respectively. Then, the vector $\\vec{x}$ perpendicular to $Y Z$ and shifting the line $Y_{0} Z_{0}$ to $Y Z$ is equal to $\\frac{1}{2} \\overrightarrow{I D}$. Define the shifting vectors $\\vec{y}=\\frac{1}{2} \\overrightarrow{I E}, \\vec{z}=\\frac{1}{2} \\overrightarrow{I F}$ similarly. Consider now the triangle $U V W$ formed by the perpendiculars to $A I, B I$, and $C I$ through $D, E$, and $F$, respectively (see figure below). This is another triangle whose sides are parallel to the corresponding sides of $X Y Z$. Claim 2. $\\overrightarrow{I U}=2 \\overrightarrow{X_{0} X}, \\overrightarrow{I V}=2 \\overrightarrow{Y_{0} Y}, \\overrightarrow{I W}=2 \\overrightarrow{Z_{0} Z}$. Proof. We prove one of the relations, the other proofs being similar. To prove the equality of two vectors it suffices to project them onto two non-parallel axes and check that their projections are equal. The projection of $\\overrightarrow{X_{0} X}$ onto $I B$ equals $\\vec{y}$, while the projection of $\\overrightarrow{I U}$ onto $I B$ is $\\overrightarrow{I E}=2 \\vec{y}$. The projections onto the other axis $I C$ are $\\vec{z}$ and $\\overrightarrow{I F}=2 \\vec{z}$. Then $\\overrightarrow{I U}=2 \\overrightarrow{X_{0} X}$ follows. Notice that the line $\\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$; thus $U, V, W$, and $I$ are concyclic. It follows from Claim 2 that $\\Varangle\\left(X X_{0}, Y Y_{0}\\right)=\\Varangle(I U, I V)=$ $\\Varangle(W U, W V)=\\Varangle\\left(Z_{0} X_{0}, Z_{0} Y_{0}\\right)$, and we are done. ", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "G5", "problem_type": "Geometry", "exam": "IMO-SL", "problem": "Let $A B C$ be a triangle with circumcircle $\\omega$ and incentre $I$. A line $\\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\\Theta$. Show that the circumcircle of the triangle $\\Theta$ is tangent to $\\omega$. (Denmark) Preamble. Let $X=y \\cap z, Y=x \\cap z, Z=x \\cap y$ and let $\\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\\Delta$ and $\\delta$ inscribed into $\\Omega$ and $\\omega$, respectively. In order to prove that $\\Omega$ and $\\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\\Delta$ to $\\delta$ lies on $\\omega$ (or $\\Omega$ ), or, in other words, to show that $\\Delta$ and $\\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\\omega$ (or $\\Omega$ ). We use directed angles throughout all the solutions.", "solution": "Let $I_{a}, I_{b}$, and $I_{c}$ be the excentres of triangle $A B C$ corresponding to $A, B$, and $C$, respectively. Also, let $u, v$, and $w$ be the lines through $D, E$, and $F$ which are perpendicular to $A I, B I$, and $C I$, respectively, and let $U V W$ be the triangle determined by these lines, where $u=V W, v=U W$ and $w=U V$ (see figure above). Notice that the line $u$ is the reflection of $I_{b} I_{c}$ in the line $x$, because $u, x$, and $I_{b} I_{c}$ are perpendicular to $A D$ and $x$ is the perpendicular bisector of $A D$. Likewise, $v$ and $I_{a} I_{c}$ are reflections of each other in $y$, while $w$ and $I_{a} I_{b}$ are reflections of each other in $z$. It follows that $X, Y$, and $Z$ are the midpoints of $U I_{a}, V I_{b}$ and $W I_{c}$, respectively, and that the triangles $U V W$, $X Y Z$ and $I_{a} I_{b} I_{c}$ are either translates of each other or homothetic with a common homothety centre. Construct the points $T$ and $S$ such that the quadrilaterals $U V I W, X Y T Z$ and $I_{a} I_{b} S I_{c}$ are homothetic. Then $T$ is the midpoint of $I S$. Moreover, note that $\\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$, hence $I$ belongs to the circumcircle of the triangle $U V W$, therefore $T$ belongs to $\\Omega$. Consider now the homothety or translation $h_{1}$ that maps $X Y Z T$ to $I_{a} I_{b} I_{c} S$ and the homothety $h_{2}$ with centre $I$ and factor $\\frac{1}{2}$. Furthermore, let $h=h_{2} \\circ h_{1}$. The transform $h$ can be a homothety or a translation, and $$ h(T)=h_{2}\\left(h_{1}(T)\\right)=h_{2}(S)=T $$ hence $T$ is a fixed point of $h$. So, $h$ is a homothety with centre $T$. Note that $h_{2}$ maps the excentres $I_{a}, I_{b}, I_{c}$ to $X_{0}, Y_{0}, Z_{0}$ defined in the preamble. Thus the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\\Omega$, and this completes the proof.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N1", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Determine all pairs $(n, k)$ of distinct positive integers such that there exists a positive integer $s$ for which the numbers of divisors of $s n$ and of $s k$ are equal. (Ukraine) Answer: All pairs $(n, k)$ such that $n \\nmid k$ and $k \\nmid n$.", "solution": "As usual, the number of divisors of a positive integer $n$ is denoted by $d(n)$. If $n=\\prod_{i} p_{i}^{\\alpha_{i}}$ is the prime factorisation of $n$, then $d(n)=\\prod_{i}\\left(\\alpha_{i}+1\\right)$. We start by showing that one cannot find any suitable number $s$ if $k \\mid n$ or $n \\mid k$ (and $k \\neq n$ ). Suppose that $n \\mid k$, and choose any positive integer $s$. Then the set of divisors of $s n$ is a proper subset of that of $s k$, hence $d(s n)<d(s k)$. Therefore, the pair $(n, k)$ does not satisfy the problem requirements. The case $k \\mid n$ is similar. Now assume that $n \\nmid k$ and $k \\nmid n$. Let $p_{1}, \\ldots, p_{t}$ be all primes dividing $n k$, and consider the prime factorisations $$ n=\\prod_{i=1}^{t} p_{i}^{\\alpha_{i}} \\quad \\text { and } \\quad k=\\prod_{i=1}^{t} p_{i}^{\\beta_{i}} $$ It is reasonable to search for the number $s$ having the form $$ s=\\prod_{i=1}^{t} p_{i}^{\\gamma_{i}} $$ The (nonnegative integer) exponents $\\gamma_{i}$ should be chosen so as to satisfy $$ \\frac{d(s n)}{d(s k)}=\\prod_{i=1}^{t} \\frac{\\alpha_{i}+\\gamma_{i}+1}{\\beta_{i}+\\gamma_{i}+1}=1 $$ First of all, if $\\alpha_{i}=\\beta_{i}$ for some $i$, then, regardless of the value of $\\gamma_{i}$, the corresponding factor in (1) equals 1 and does not affect the product. So we may assume that there is no such index $i$. For the other factors in (1), the following lemma is useful. Lemma. Let $\\alpha>\\beta$ be nonnegative integers. Then, for every integer $M \\geqslant \\beta+1$, there exists a nonnegative integer $\\gamma$ such that $$ \\frac{\\alpha+\\gamma+1}{\\beta+\\gamma+1}=1+\\frac{1}{M}=\\frac{M+1}{M} . $$ Proof. $$ \\frac{\\alpha+\\gamma+1}{\\beta+\\gamma+1}=1+\\frac{1}{M} \\Longleftrightarrow \\frac{\\alpha-\\beta}{\\beta+\\gamma+1}=\\frac{1}{M} \\Longleftrightarrow \\gamma=M(\\alpha-\\beta)-(\\beta+1) \\geqslant 0 . $$ Now we can finish the solution. Without loss of generality, there exists an index $u$ such that $\\alpha_{i}>\\beta_{i}$ for $i=1,2, \\ldots, u$, and $\\alpha_{i}<\\beta_{i}$ for $i=u+1, \\ldots, t$. The conditions $n \\nmid k$ and $k \\nmid n$ mean that $1 \\leqslant u \\leqslant t-1$. Choose an integer $X$ greater than all the $\\alpha_{i}$ and $\\beta_{i}$. By the lemma, we can define the numbers $\\gamma_{i}$ so as to satisfy $$ \\begin{array}{ll} \\frac{\\alpha_{i}+\\gamma_{i}+1}{\\beta_{i}+\\gamma_{i}+1}=\\frac{u X+i}{u X+i-1} & \\text { for } i=1,2, \\ldots, u, \\text { and } \\\\ \\frac{\\beta_{u+i}+\\gamma_{u+i}+1}{\\alpha_{u+i}+\\gamma_{u+i}+1}=\\frac{(t-u) X+i}{(t-u) X+i-1} & \\text { for } i=1,2, \\ldots, t-u . \\end{array} $$ Then we will have $$ \\frac{d(s n)}{d(s k)}=\\prod_{i=1}^{u} \\frac{u X+i}{u X+i-1} \\cdot \\prod_{i=1}^{t-u} \\frac{(t-u) X+i-1}{(t-u) X+i}=\\frac{u(X+1)}{u X} \\cdot \\frac{(t-u) X}{(t-u)(X+1)}=1, $$ as required. Comment. The lemma can be used in various ways, in order to provide a suitable value of $s$. In particular, one may apply induction on the number $t$ of prime factors, using identities like $$ \\frac{n}{n-1}=\\frac{n^{2}}{n^{2}-1} \\cdot \\frac{n+1}{n} $$", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N5", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t . $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia) Answer: No.", "solution": "Arguing indirectly, assume that $x y=a^{2}$ and $z t=c^{2}$ with $a, c>0$. Suppose that the number $x+y=z+t$ is odd. Then $x$ and $y$ have opposite parity, as well as $z$ and $t$. This means that both $x y$ and $z t$ are even, as well as $x y-z t=x+y$; a contradiction. Thus, $x+y$ is even, so the number $s=\\frac{x+y}{2}=\\frac{z+t}{2}$ is a positive integer. Next, we set $b=\\frac{|x-y|}{2}, d=\\frac{|z-t|}{2}$. Now the problem conditions yield $$ s^{2}=a^{2}+b^{2}=c^{2}+d^{2} $$ and $$ 2 s=a^{2}-c^{2}=d^{2}-b^{2} $$ (the last equality in (2) follows from (1)). We readily get from (2) that $a, d>0$. In the sequel we will use only the relations (1) and (2), along with the fact that $a, d, s$ are positive integers, while $b$ and $c$ are nonnegative integers, at most one of which may be zero. Since both relations are symmetric with respect to the simultaneous swappings $a \\leftrightarrow d$ and $b \\leftrightarrow c$, we assume, without loss of generality, that $b \\geqslant c$ (and hence $b>0$ ). Therefore, $d^{2}=2 s+b^{2}>c^{2}$, whence $$ d^{2}>\\frac{c^{2}+d^{2}}{2}=\\frac{s^{2}}{2} $$ On the other hand, since $d^{2}-b^{2}$ is even by (2), the numbers $b$ and $d$ have the same parity, so $0<b \\leqslant d-2$. Therefore, $$ 2 s=d^{2}-b^{2} \\geqslant d^{2}-(d-2)^{2}=4(d-1), \\quad \\text { i.e., } \\quad d \\leqslant \\frac{s}{2}+1 $$ Combining (3) and (4) we obtain $$ 2 s^{2}<4 d^{2} \\leqslant 4\\left(\\frac{s}{2}+1\\right)^{2}, \\quad \\text { or } \\quad(s-2)^{2}<8 $$ which yields $s \\leqslant 4$. Finally, an easy check shows that each number of the form $s^{2}$ with $1 \\leqslant s \\leqslant 4$ has a unique representation as a sum of two squares, namely $s^{2}=s^{2}+0^{2}$. Thus, (1) along with $a, d>0$ imply $b=c=0$, which is impossible.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N5", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t . $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia) Answer: No.", "solution": "We start with a complete description of all 4-tuples $(x, y, z, t)$ of positive integers satisfying (*). As in the solution above, we notice that the numbers $$ s=\\frac{x+y}{2}=\\frac{z+t}{2}, \\quad p=\\frac{x-y}{2}, \\quad \\text { and } \\quad q=\\frac{z-t}{2} $$ are integers (we may, and will, assume that $p, q \\geqslant 0$ ). We have $$ 2 s=x y-z t=(s+p)(s-p)-(s+q)(s-q)=q^{2}-p^{2} $$ so $p$ and $q$ have the same parity, and $q>p$. Set now $k=\\frac{q-p}{2}, \\ell=\\frac{q+p}{2}$. Then we have $s=\\frac{q^{2}-p^{2}}{2}=2 k \\ell$ and hence $$ \\begin{array}{rlrl} x & =s+p=2 k \\ell-k+\\ell, & y & =s-p=2 k \\ell+k-\\ell, \\\\ z & =s+q=2 k \\ell+k+\\ell, & t=s-q=2 k \\ell-k-\\ell . \\end{array} $$ Recall here that $\\ell \\geqslant k>0$ and, moreover, $(k, \\ell) \\neq(1,1)$, since otherwise $t=0$. Assume now that both $x y$ and $z t$ are squares. Then $x y z t$ is also a square. On the other hand, we have $$ \\begin{aligned} x y z t=(2 k \\ell-k+\\ell) & (2 k \\ell+k-\\ell)(2 k \\ell+k+\\ell)(2 k \\ell-k-\\ell) \\\\ & =\\left(4 k^{2} \\ell^{2}-(k-\\ell)^{2}\\right)\\left(4 k^{2} \\ell^{2}-(k+\\ell)^{2}\\right)=\\left(4 k^{2} \\ell^{2}-k^{2}-\\ell^{2}\\right)^{2}-4 k^{2} \\ell^{2} \\end{aligned} $$ Denote $D=4 k^{2} \\ell^{2}-k^{2}-\\ell^{2}>0$. From (6) we get $D^{2}>x y z t$. On the other hand, $$ \\begin{array}{r} (D-1)^{2}=D^{2}-2\\left(4 k^{2} \\ell^{2}-k^{2}-\\ell^{2}\\right)+1=\\left(D^{2}-4 k^{2} \\ell^{2}\\right)-\\left(2 k^{2}-1\\right)\\left(2 \\ell^{2}-1\\right)+2 \\\\ =x y z t-\\left(2 k^{2}-1\\right)\\left(2 \\ell^{2}-1\\right)+2<x y z t \\end{array} $$ since $\\ell \\geqslant 2$ and $k \\geqslant 1$. Thus $(D-1)^{2}<x y z t<D^{2}$, and $x y z t$ cannot be a perfect square; a contradiction. Comment. The first part of Solution 2 shows that all 4-tuples of positive integers $x \\geqslant y, z \\geqslant t$ satisfying (*) have the form (5), where $\\ell \\geqslant k>0$ and $\\ell \\geqslant 2$. The converse is also true: every pair of positive integers $\\ell \\geqslant k>0$, except for the pair $k=\\ell=1$, generates via (5) a 4-tuple of positive integers satisfying $(*)$.", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |
| {"year": "2018", "tier": "T0", "problem_label": "N7", "problem_type": "Number Theory", "exam": "IMO-SL", "problem": "Let $n \\geqslant 2018$ be an integer, and let $a_{1}, a_{2}, \\ldots, a_{n}, b_{1}, b_{2}, \\ldots, b_{n}$ be pairwise distinct positive integers not exceeding $5 n$. Suppose that the sequence $$ \\frac{a_{1}}{b_{1}}, \\frac{a_{2}}{b_{2}}, \\ldots, \\frac{a_{n}}{b_{n}} $$ forms an arithmetic progression. Prove that the terms of the sequence are equal. (Thailand)", "solution": "Suppose that (1) is an arithmetic progression with nonzero difference. Let the difference be $\\Delta=\\frac{c}{d}$, where $d>0$ and $c, d$ are coprime. We will show that too many denominators $b_{i}$ should be divisible by $d$. To this end, for any $1 \\leqslant i \\leqslant n$ and any prime divisor $p$ of $d$, say that the index $i$ is $p$-wrong, if $v_{p}\\left(b_{i}\\right)<v_{p}(d)$. $\\left(v_{p}(x)\\right.$ stands for the exponent of $p$ in the prime factorisation of $x$.) Claim 1. For any prime $p$, all $p$-wrong indices are congruent modulo $p$. In other words, the $p$-wrong indices (if they exist) are included in an arithmetic progression with difference $p$. Proof. Let $\\alpha=v_{p}(d)$. For the sake of contradiction, suppose that $i$ and $j$ are $p$-wrong indices (i.e., none of $b_{i}$ and $b_{j}$ is divisible by $\\left.p^{\\alpha}\\right)$ such that $i \\not \\equiv j(\\bmod p)$. Then the least common denominator of $\\frac{a_{i}}{b_{i}}$ and $\\frac{a_{j}}{b_{j}}$ is not divisible by $p^{\\alpha}$. But this is impossible because in their difference, $(i-j) \\Delta=\\frac{(i-j) c}{d}$, the numerator is coprime to $p$, but $p^{\\alpha}$ divides the denominator $d$. Claim 2. $d$ has no prime divisors greater than 5 . Proof. Suppose that $p \\geqslant 7$ is a prime divisor of $d$. Among the indices $1,2, \\ldots, n$, at most $\\left\\lceil\\frac{n}{p}\\right\\rceil<\\frac{n}{p}+1$ are $p$-wrong, so $p$ divides at least $\\frac{p-1}{p} n-1$ of $b_{1}, \\ldots, b_{n}$. Since these denominators are distinct, $$ 5 n \\geqslant \\max \\left\\{b_{i}: p \\mid b_{i}\\right\\} \\geqslant\\left(\\frac{p-1}{p} n-1\\right) p=(p-1)(n-1)-1 \\geqslant 6(n-1)-1>5 n, $$ a contradiction. Claim 3. For every $0 \\leqslant k \\leqslant n-30$, among the denominators $b_{k+1}, b_{k+2}, \\ldots, b_{k+30}$, at least $\\varphi(30)=8$ are divisible by $d$. Proof. By Claim 1, the 2 -wrong, 3 -wrong and 5 -wrong indices can be covered by three arithmetic progressions with differences 2,3 and 5 . By a simple inclusion-exclusion, $(2-1) \\cdot(3-1) \\cdot(5-1)=8$ indices are not covered; by Claim 2, we have $d \\mid b_{i}$ for every uncovered index $i$. Claim 4. $|\\Delta|<\\frac{20}{n-2}$ and $d>\\frac{n-2}{20}$. Proof. From the sequence (1), remove all fractions with $b_{n}<\\frac{n}{2}$, There remain at least $\\frac{n}{2}$ fractions, and they cannot exceed $\\frac{5 n}{n / 2}=10$. So we have at least $\\frac{n}{2}$ elements of the arithmetic progression (1) in the interval $(0,10]$, hence the difference must be below $\\frac{10}{n / 2-1}=\\frac{20}{n-2}$. The second inequality follows from $\\frac{1}{d} \\leqslant \\frac{|c|}{d}=|\\Delta|$. Now we have everything to get the final contradiction. By Claim 3, we have $d \\mid b_{i}$ for at least $\\left\\lfloor\\frac{n}{30}\\right\\rfloor \\cdot 8$ indices $i$. By Claim 4 , we have $d \\geqslant \\frac{n-2}{20}$. Therefore, $$ 5 n \\geqslant \\max \\left\\{b_{i}: d \\mid b_{i}\\right\\} \\geqslant\\left(\\left\\lfloor\\frac{n}{30}\\right\\rfloor \\cdot 8\\right) \\cdot d>\\left(\\frac{n}{30}-1\\right) \\cdot 8 \\cdot \\frac{n-2}{20}>5 n . $$ Comment 1. It is possible that all terms in (1) are equal, for example with $a_{i}=2 i-1$ and $b_{i}=4 i-2$ we have $\\frac{a_{i}}{b_{i}}=\\frac{1}{2}$. Comment 2. The bound $5 n$ in the statement is far from sharp; the solution above can be modified to work for $9 n$. For large $n$, the bound $5 n$ can be replaced by $n^{\\frac{3}{2}-\\varepsilon}$. The activities of the Problem Selection Committee were supported by DEDEMAN LA FANTANA vine la tine", "metadata": {"resource_path": "IMO_SL/segmented/en-IMO2018SL.jsonl"}} | |