OLYMPIADES FRANÇAISES DE MATHÉMATIQUES
TEST DE JANVIER - CORRIGÉ
MERCREDI 15 JANVIER 2014 DURÉE: 4 HEURES
\section*{Exercices du groupe B}
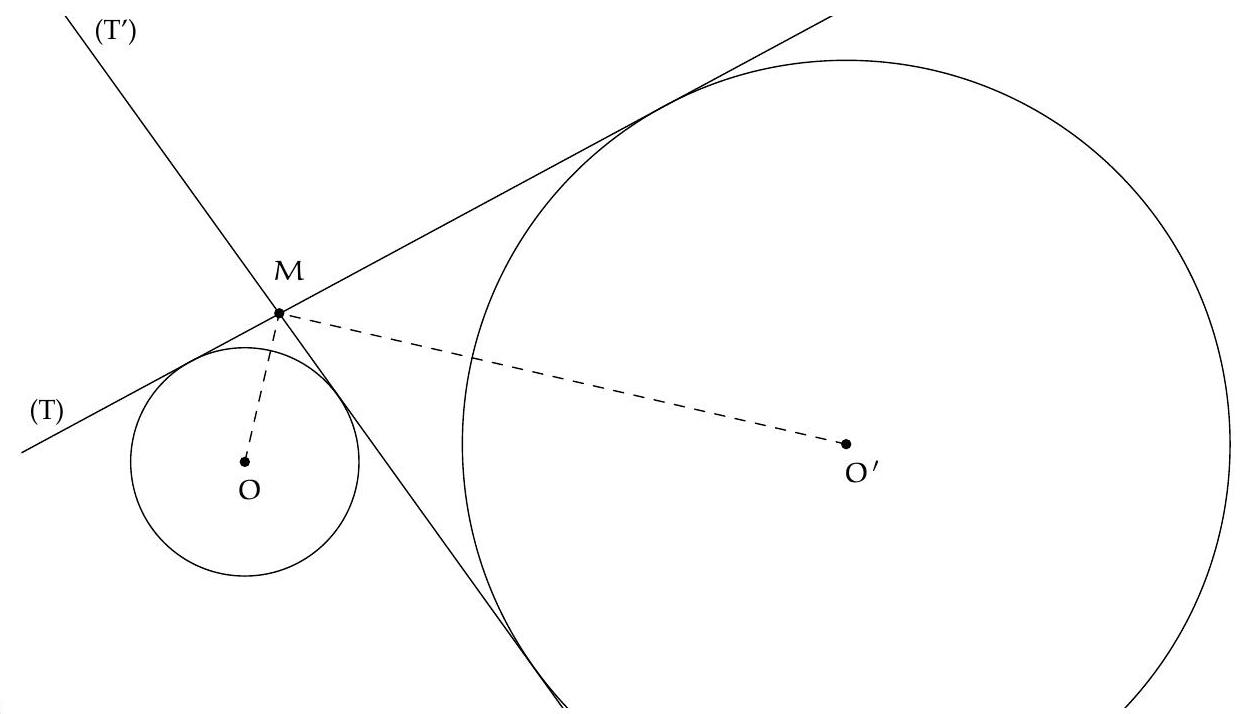
Exercice 1. Soient $C$ et $\mathrm{C}^{\prime}$ deux cercles de centres $O$ et $\mathrm{O}^{\prime}$, extérieurs l'un à l'autre. Une tangente commune extérieure coupe les deux tangentes communes intérieures aux points M et N .
Montrer que (OM) est perpendiculaire à ( $O^{\prime} M$ ) et que ( $O N$ ) est perpendiculaire à ( $O^{\prime} N$ ).
Solution de l'exercice 1
Soit (T) la tangente commune extérieure de l'énoncé. Soit ( $\mathrm{T}^{\prime}$ ) la tangente commune intérieure passant par $M$. Les droites $(T)$ et $\left(T^{\prime}\right)$ sont donc les deux tangentes à $C$ issues de $M$.
Comme ces deux tangentes sont symétriques par rapport à (OM), la droite (OM) est une bissectrice de ( $T$ ) et $\left(T^{\prime}\right)$. De même, $\left(O^{\prime} M\right.$ ) est une bissectrice de $(T)$ et $\left(T^{\prime}\right)$.
Comme les bissectrices de deux droites sont perpendiculaires, $(O M)$ et $\left(O^{\prime} M\right.$ ) sont perpendiculaires ou confondues.
Si elles étaient confondues, $\mathrm{O}, \mathrm{O}^{\prime}, \mathrm{M}$ seraient alignés, et les deux tangentes à ( C ) passant par $M$ seraient extérieures, ce qui n'est pas le cas.
Par conséquent, $(O M) \perp\left(O^{\prime} M\right)$. On montre de même que $(O N) \perp\left(O^{\prime} N\right)$. Exercice 2. Soit $k \geqslant 1$ un entier. À chaque client, un opérateur téléphonique propose $k$ numéros pour lesquels la communication est gratuite (si une personne $A$ choisit le numéro de $B$, alors les appels de $A$ vers $B$ et de $B$ vers $A$ sont gratuits). On considère un groupe de $n$ personnes.
- Si $n \geqslant 2 k+2$, montrer qu'il existe deux personnes qui ne pourront pas communiquer gratuitement.
- $\operatorname{Si} n=2 k+1$, montrer que les $n$ personnes peuvent faire en sorte que toute personne peut communiquer gratuitement avec n'importe quelle autre. Solution de l'exercice 2 On dira pour simplifier qu'une personne $A$ choisit une personne B si le numéro de $B$ fait parti des numéros choisis par $A$ vers lesquels la communication est gratuite.
- Comme chaque personne peut choisir au plus k autre personnes, il y a au plus kn paires de personnes qui peuvent communiquer gratuitement. Or le nombre total de paires de personnes est $n(n-1) / 2$, et on a
Ainsi, le nombre total de paires de personnes est strictement supérieur au nombre de paires de personnes qui peuvent communiquer gratuitement. Il existe donc forcément deux personnes qui ne pourront pas communiquer gratuitement. 2) Plaçons les $2 k+1$ personnes sur un cercle. Chaque personne choisit alors de communiquer gratuitement avec les $k$ personnes qui sont situées juste après elle. On vérifie aisément que cette configuration permet à toute personne de communiquer gratuitement avec n'importe quelle autre : par construction, chaque personne peut communiquer avec les $k$ personnes situées juste après elle ainsi qu'avec les $k$ personnes situées juste avant elles, autrement dit tout le monde.
Exercice 3. Soit $n \geqslant 1$ un entier. Déterminer tous les entiers $p \geqslant 1$ pour lesquels il existe des entiers strictement positifs $x_{1}<x_{2}<\cdots<x_{n}$ tels que
Solution de l'exercice 3 Nous allons montrer que l'ensemble des solutions est l'ensemble ${1,2, \ldots, n}$. Soient $p \geqslant 1$ un entier et des entiers strictement positifs $x_{1}<x_{2}<\cdots<x_{n}$ tels que
On remarque tout d'abord que $p \leqslant n$. En effet, si $i$ et $j$ sont deux entiers tels que $i>j$, alors $i \geqslant j+1$. On en déduit que $x_{i} \geqslant i$ pour tout entier $1 \leqslant i \leqslant n$. Ainsi
Donc $p \leqslant n$. Réciproquement, soit $1 \leqslant p \leqslant \mathrm{n}$ et montrons qu'il existe des entiers strictement positifs $x_{1}<x_{2}<\cdots<x_{n}$ tels que
Pour cela, on choisit les $x_{i}$ de sorte que parmi les différents quotients $i / x_{i}(1 \leqslant i \leqslant n)$ on ait $p-1$ quotients égaux à 1 et les $n-p+1$ autres égaux à $1 /(n-p+1)$. Plus précisément, on choisit: $x_{1}=1, x_{2}=2, \ldots, x_{p-1}=p-1, x_{p}=p(n-p+1), x_{p+1}=(p+1)(n-p+1), \ldots, x_{n}=n(n-p+1)$.
On vérifie aisément que $x_{1}<x_{2}<\cdots<x_{n}$ et que
Exercice commun
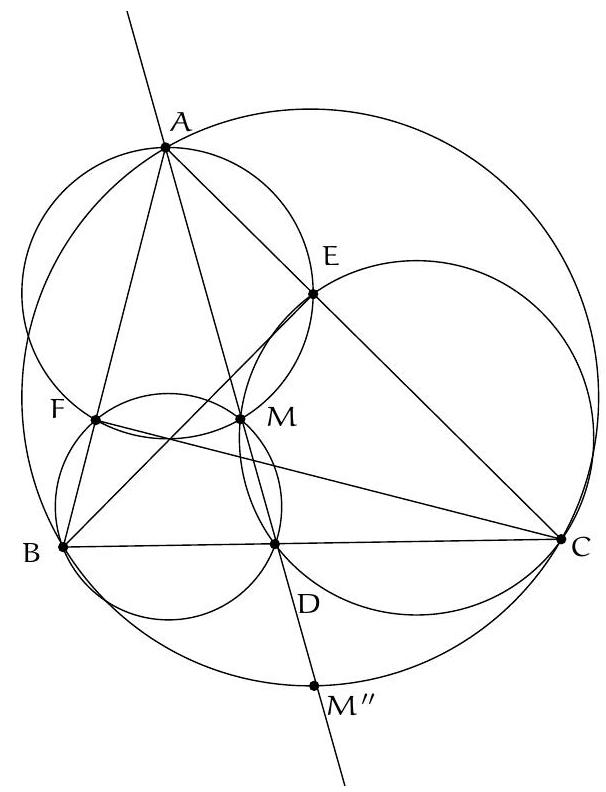
Exercice 4. Soit $A B C$ un triangle dont les angles sont aigus, et tel que $A B \neq A C$. On note $D$ le pied de la bissectrice de $\widehat{B A C}$. Le point $E$ (resp. $F$ ) désigne le pied de la hauteur issue de $B$ (resp. de C). Le cercle circonscrit au triangle DBF rencontre le cercle circonscrit au triangle DCE en un point $M$ autre que $D$.
Prouver que ME $=M F$.
Solution de l'exercice 4
Lemme 1. Les cercles AEF, BDF et CDE sont concourants en $M$. Cela découle immédiatement du théorème de Miquel mais rappelons tout de même la démonstration: $(M F, M E)=(M F, M D)+(M D, M E)=(B F, B D)+(C D, C E)=(A B, C D)+(C D, A C)=$ ( $A B, A C$ ) donc $A, E, F, M$ sont cocycliques.
Lemme 2. Les triangles $A E F$ et $A B C$ sont (indirectement) semblables. Les triangles $A F C$ et $A E B$ sont rectangles en $F$ et en $E$, et leurs angles en $A$ sont égaux, donc ils sont semblables. On en déduit que $\frac{A E}{A F}=\frac{A B}{A C}$. Ceci s'écrit encore $\frac{A E}{A B}=\frac{A F}{A C}$. Comme $\widehat{E A F}=\widehat{B A C}$, les triangles EAF et $B A C$ sont semblables. Il est clair que la similitude est indirecte puisque les angles orientés $(\overrightarrow{A B}, \overrightarrow{A C})$ et $(\overrightarrow{A E}, \overrightarrow{A F})$ sont opposés.
Revenons à l'exercice. Soit $M^{\prime}$ le point d'intersection autre que $A$ entre la bissectrice de $\widehat{B A C}$ et le cercle $A E F$. De même, on définit $M^{\prime \prime}$ comme le point d'intersection autre que $A$ entre la bissectrice de $\widehat{B A C}$ et le cercle $A B C$. Montrons que $M^{\prime}=M$.
On en déduit que $M^{\prime}$ appartient au cercle BDF. De même, il appartient au cercle CDE. Par conséquent, il est l'intersection des trois cercles BDF, CDE et $A E F$ : ceci prouve que $M^{\prime}=M$.
Enfin, comme les arcs MF et ME sont égaux (puisque (AM) est la bissectrice de $\widehat{F A E}$ ), on a $M F=M E$.
Autre solution.
Lemme 1. Deux cordes $\left[\mathrm{BB}^{\prime}\right]$ et $\left[\mathrm{CC}^{\prime}\right]$ d'un cercle se coupent en un point extérieur $A$. Alors les triangles $A B C$ et $A C^{\prime} B^{\prime}$ sont indirectement semblables.
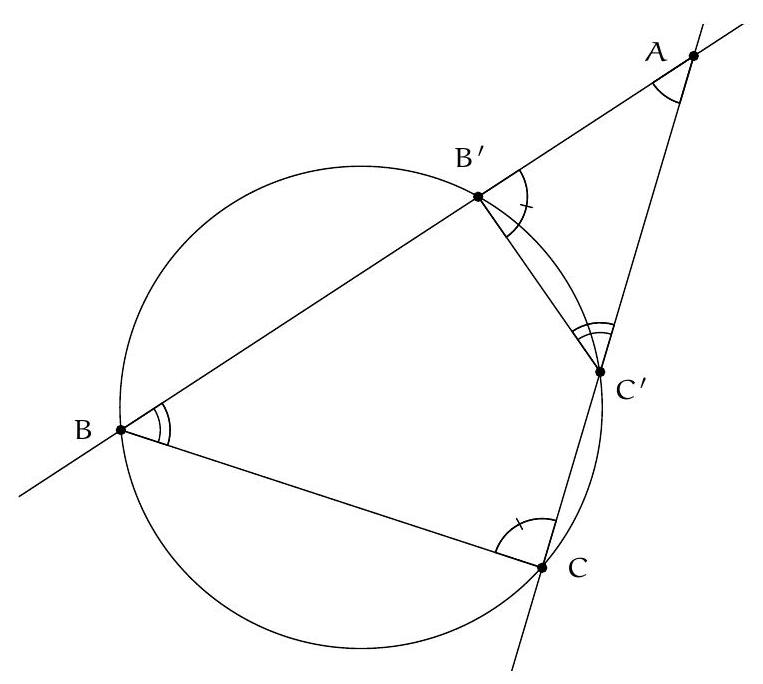
On a $\left(B^{\prime} C^{\prime}, B^{\prime} A\right)=\left(B^{\prime} C^{\prime}, B^{\prime} B\right)=\left(C C^{\prime}, C B\right)=(C A, C B)$ et de même $\left(C^{\prime} A, C^{\prime} B^{\prime}\right)=(B C, B A)$. Lemme 2. $\frac{D B}{D C}=\frac{A B}{A C}$. D'après la loi des sinus, on a $\frac{A B}{D B}=\frac{\sin \widehat{A D B}}{\sin \frac{\widehat{B A C}}{2}}=\frac{\sin \widehat{C D A}}{\sin \frac{\widehat{B A C}}{2}}=\frac{A C}{D C}$. Revenons à l'exercice. Comme AFC et AEB sont rectangles en $F$ et $E$ et ont le même angle en $A$, ils sont semblables. On en déduit $\frac{A F}{A E}=\frac{A C}{A B}$, ce qui s'écrit encore $A F \cdot A B=A E \cdot A C$. Autrement dit, $A$ a la même puissance par rapport aux deux cercles BFD et CED. Par conséquent, $A$ se trouve sur l'axe radical (MD). $D^{\prime}$ 'autre part, le lemme 1 entraîne que $A F M$ et $A D B$ sont semblables, donc $\frac{B D}{B A}=\frac{M F}{M A}$. De même, $\frac{C D}{C A}=\frac{M E}{M A}$. D'après le lemme 2 , on a $\frac{B D}{B A}=\frac{C D}{C A}$ donc $M F=M E$.
Exercices du groupe A
Exercice 5. On dit qu'une suite $\left(u_{n}\right){n \geqslant 1}$ est Sicilienne si $u{1}$ est un entier strictement positif, et si pour tout $n$,
Existe-t-il une suite Sicilienne $\left(u_{n}\right){n \geqslant 1}$ telle que $u{n}>1$ pour tout $n$ ? (N.B. $[x]$ désigne la partie entière de $x$. Par exemple, $[2,71828]=2$.)
Solution de l'exercice 5 Commençons par une simple remarque. Soit $\mathrm{f}: \mathbb{N}^{} \rightarrow \mathbb{N}^{}$ la fonction qui, à tout entier naturel non nul $n$, associe l'entier $n / 2$ si $n$ est pair, et $n+[\sqrt{n}]$ si $n$ est impair. Il est clair que l'image $f(n)$ est bien un entier naturel non nul.
Nous allons maintenant montrer que la réponse à la question de l'énoncé est négative : toute suite Sicilienne $\left(u_{n}\right){n \geqslant 1}$ contient un terme $u{n}=1$.
Soit $\left(u_{n}\right){n \geqslant 1}$ une suite Sicilienne : on note que $u{n+1}=f\left(u_{n}\right)$ pour tout entier $n \geqslant 1$. Soit alors $E=\left{u_{n} \mid n \geqslant 1\right}$ l'ensemble des valeurs prises par les termes de cette suite. $E$ est un ensemble d'entiers non vide, de sorte qu'il admet un minimum $M$, tel que $M \geqslant 1$ : il existe alors un entier $n \geqslant 1$ tel que $M=u_{n}$. Notre but est de montrer que $M=1$. Nous allons donc procéder par l'absurde, et supposer que $M \geqslant 2$.
Si $M$ est pair, alors $u_{n+1}=f\left(u_{n}\right)=f(M)=M / 2<M$ et, puisque $u_{n+1} \in E$, cela contredit la minimalité de $M$.
Si $M$ est impair, soit $k$ l'entier naturel non nul tel que $k^{2} \leqslant M<(k+1)^{2}$. Si $k$ est impair, alors $u_{n+1}=f(M)=M+k$, donc $M+k$ est pair, et $u_{n+2}=f\left(u_{n+1}\right)=f(M+k)=\frac{M+k}{2}$. Or, $M>1$, donc $M-k \geqslant M-\sqrt{M}=\sqrt{M}(\sqrt{M}-1)>0$, de sorte que $u_{n+2}<M$ : puisque $u_{n+2} \in E$, cela contredit la minimalité de $M$.
Ainsi, on sait que $M$ est impair et que $k$ est pair, donc que $k^{2}+1 \leqslant M<(k+1)^{2}$.
- Si $k^{2}+1 \leqslant M \leqslant k^{2}+k$, alors $k^{2} \leqslant f(M)=M+k<(k+1)^{2}$, puis $(k+1)^{2} \leqslant f^{2}(M)=$ $M+2 k<(k+2)^{2}$, donc $f^{3}(M)=M+3 k+1$ est pair, et enfin $f^{4}(M)=\frac{M+3 k+1}{2}$.
- Si $k^{2}+k+1 \leqslant M<(k+1)^{2}$, alors $(k+1)^{2} \leqslant f(M)=M+k<(k+2)^{2}$, donc $f^{2}(M)=$ $M+2 k+1$ est pair, et enfin $f^{3}(M)=\frac{M+2 k+1}{2}$. Il s'ensuit que $M=\min E \leqslant \min \left{f^{3}(M), f^{4}(M)\right} \leqslant \frac{M+3 k+1}{2}$, donc que $M \leqslant 3 k+1$. En particulier, $k^{2} \leqslant 3 k+1$, ce qui signifie que $k^{2}-3 k-1=\left(k-\frac{3}{2}\right)^{2}-\frac{13}{4} \leqslant 0$, donc que $k \leqslant \frac{3}{2}+\sqrt{\frac{13}{4}}<2+\sqrt{4}=4$. Puisque $k$ est pair et $M$ impair, en déduit que $k=2$ et que $M \in{5,7}$. On conclut donc l'exercice en montrant que $\mathbf{f}^{5}(5)=3<5$ et que $\mathrm{f}^{4}(7)=3<7$, ce qui permet bien d'établir que nulle valeur $M \geqslant 2$ n'est possible. Exercice 6. Déterminer tous les couples d'entiers positifs ou nuls $(x, y)$ pour lesquels $x^{2}+y^{2}$ divise à la fois $x^{3}+y$ et $x+y^{3}$. Solution de l'exercice 6 Tout d'abord, remarquons que les couples $(x, y) \in{(0,0),(1,0),(0,1),(1,1)}$ sont solutions.
On se place maintenant dans le cas où $(x, y)$ est une solution éventuelle autre que celles-ci. De plus, $x$ et $y$ jouant des rôles symétriques, on suppose ici que $x \leqslant y$, donc que $y \geqslant 2$. Si $x=0$, le problème revient à trouver $y$ tel que $y^{2}$ divise à la fois $y$ et $y^{3}$, ce qui est incompatible avec la contrainte $y \geqslant 2$. Ainsi, $y \geqslant 2$ et $x \geqslant 1$, donc $x y-1 \geqslant 1$.
Soit alors $d$ le PGCD de $x$ et $y$ : on note $x=d X$ et $y=d Y$, avec $X$ et $Y$ premiers entre eux : notons que $d>0$ et que $X^{2}+Y^{2}>0$. Il s'ensuit que $d\left(X^{2}+Y^{2}\right)$ divise à la fois $d^{2} X^{3}+Y$ et $X+d^{2} Y^{3}$. En particulier, $d$ divise à la fois $X$ et $Y$, donc $d=1$. Par conséquent, $\operatorname{PGCD}\left(x^{2}+y^{2}, x\right)=$ $\operatorname{PGCD}\left(\mathrm{y}^{2}, \mathrm{x}\right)=1$.
En outre, $x^{2}+y^{2}$ divise $y\left(x^{3}+y\right)-\left(x^{2}+y^{2}\right)=x^{2}(x y-1)$, de sorte que, d'après le théorème de Gauss, $x^{2}+y^{2}$ divise $x y-1$. Puisque $x y-1 \neq 0$, on en déduit que $x^{2}+y^{2} \leqslant x y-1$. Or, $x^{2}+y^{2}=(x y-1)+\left(x y+1+(x-y)^{2}\right)>x y-1$. On a ainsi montré que les quatre solutions sus-mentionnées sont les seules solutions au problème.
Exercice 7. On répartit des poids de respectivement $1 \mathrm{g}, 2 \mathrm{g}, \ldots, 200 \mathrm{~g}$ sur les deux plateaux d'une balance de sorte que chaque plateau contienne 100 poids.
Prouver que l'on peut échanger 50 poids d'un plateau avec 50 poids de l'autre plateau pour que la balance devienne équilibrée. Solution de l'exercice 7 Dans cette solution, on dira que deux poids sont complémentaires s'ils pèsent 201 grammes à eux deux.
Considérons alors les 100 poids situés sur le plateau de gauche. On peut les classer en trois catégories:
- les poids $a_{1}, \ldots, a_{n}$ de 100 grammes ou moins, dont le complémentaire est également sur le plateau de gauche;
- leurs complémentaires, qui sont les poids $A_{1}, \ldots, A_{n}$ de 101 grammes ou plus, dont le complémentaire est également sur le plateau de gauche (avec $A_{k}=201-a_{k}$ );
- enfin, les poids $b_{1}, \ldots, b_{\ell}$ dont le complémentaire est sur le plateau de droite.
De même, on peut classer les 100 poids du plateau de droite en trois catégories :
- les poids $c_{1}, \ldots, c_{m}$ de 100 grammes ou moins, dont le complémentaire est également sur le plateau de droite;
- leurs complémentaires, qui sont les poids $C_{1}, \ldots, C_{m}$ de 101 grammes ou plus, dont le complémentaire est également sur le plateau de gauche ; (avec $\mathrm{C}{\mathrm{k}}=201-\mathrm{c}{\mathrm{k}}$ );
- enfin, les poids $B_{1}, \ldots, B_{\ell}$ qui sont les complémentaires des poids $b_{1}, \ldots, b_{\ell}$ (avec $B_{k}=$ $201-b_{k}$ ) ; ce sont les poids du plateau de droite dont le complémentaire est sur le plateau de gauche. Notons que $100=2 \mathrm{n}+\ell=2 \mathrm{~m}+\ell$, de sorte que $\mathrm{m}=\mathrm{n}$. Deux possibilités s'offrent alors à nous:
- si $m=n \geqslant 25$, on conserve sur le plateau de gauche les 50 poids $a_{1}, \ldots, a_{25}$ et $A_{1}, \ldots, A_{25}$, et on $y$ transfère les 50 poids $c_{1}, \ldots, c_{25}$ et $C_{1}, \ldots, C_{25}$; tous les autres poids sont mis sur le plateau de droite;
- si $\mathrm{m}=\mathrm{n}<25$, cela signifie que $\ell>50$; dans ce cas, on conserve sur le plateau de gauche les 50 poids $b_{1}, \ldots, b_{50}$ et on y transfère les 50 poids $B_{1}, \ldots, B_{50}$; tous les autres poids sont mis sur le plateau de droite. Dans les deux cas, on a transféré 50 poids du plateau de gauche vers le plateau de droite, et réciproquement. En outre, chacun des deux plateaux est maintenant formé de 50 paires de poids complémentaires, de sorte que chacune pèse $50 \times 201$ grammes, et donc qu'elles ont bien le même poids.