French/md/tests/fr-2018-2019-Test-15-05-Corrigé.md

PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES

TEST DU 15 MAI 2019
DURÉE: 4H

Instructions

$\triangleright$ Le groupe Junior est constitué des élèves nés en 2004 ou après. Le groupe Senior est constitué des élèves nés en 2003 ou avant. $\triangleright$ Les exercices 1 à 4 ne concernent que les élèves du groupe Junior. Les exercices 5 à 7 ne concernent que les élèves du groupe Senior. $\triangleright$ Rédigez les différents problèmes sur des copies distinctes. Sur chaque copie, écrivez en haut à gauche votre nom en majuscules, votre prénom en minuscules. Écrivez votre classe et le numéro du problème traité en haut à droite. $\triangleright$ On demande des solutions complètement rédigées, où toute affirmation est soigneusement justifiée. La notation tiendra compte de la clarté et de la précision de la copie. Travaillez d'abord au brouillon, et rédigez ensuite au propre votre solution, ou une tentative, rédigée, de solution contenant des résultats significatifs pour le problème. Ne rendez pas vos brouillons : ils ne seraient pas pris en compte. $\triangleright$ Une solution complète rapportera plus de points que plusieurs tentatives inachevées. Il vaut mieux terminer un petit nombre de problèmes que de tous les aborder. $\triangleright$ Règles, équerres et compas sont autorisés. Les rapporteurs sont interdits. Les calculatrices sont interdites, ainsi que tous les instruments électroniques. Chaque exercice est noté sur 7 points.

^0

Exercices du groupe Junior

Exercice 1. Soit $S$ un ensemble d'entiers. On dit que $S$ est insommable si, pour tous les entiers $x$ et $y$ appartenant à $S$, la somme $x+y$ n'appartient pas à $S$. Pour tout entier $n \geqslant 1$, on note $s_{n}$ le nombre de sous-ensembles de ${1,2, \ldots, 2 n}$ qui sont insommables. Démontrer que $s_{n} \geqslant 2^{n}$. Solution de l'exercice 1 Soit $S$ une partie de ${n+1, \ldots, 2 n}$. Une telle partie est insommable, puisque, pour tous les entiers $x, y$ et $z$ appartenant à $S$, on a $x+y \geqslant 2(n+1)>2 n \geqslant z$. Or, il existe $2^{n}$ parties de ${n+1, \ldots, 2 n}$. On en déduit bien que $s_{n} \geqslant 2^{n}$.

Note : On peut en fait démontrer que $2^{\mathfrak{n}+4} \geqslant s_{n} \geqslant 2^{\mathfrak{n}+1}$ pour tout $n \geqslant 3$. L'inégalité $s_{n} \geqslant$ $2^{\mathrm{n}+1}$ s'obtient, par exemple, comme suit. Pour tout entier $k \in{1, \ldots, 2 \mathfrak{n}}$, on note $E_{k}$ l'ensemble des parties de ${\lfloor k / 2\rfloor+1, \ldots, k}$ auxquelles appartient $k$. $S i$ un ensemble $S$ appartient à $E_{k}$, alors pour tous $x$ et $y$ appartenant à $S$, on a bien $x+y \geqslant 2\lfloor k / 2\rfloor+2>k=\max S$, donc $S$ est insommable. Or, $E_{k}$ contient exactement $2^{k-\lfloor k / 2\rfloor-1}$ ensembles, et $k$ est l'élément maximum de tout ensemble $S$ appartenant à $E_{k}$, donc les ensembles $E_{k}$ sont deux à deux disjoints. Si on pose $k=2 \ell-\varepsilon$, avec $\varepsilon=0$ ou $\varepsilon=1$, on a alors $k-\lfloor k / 2\rfloor-1=2 \ell-\varepsilon-(\ell-\varepsilon)-1=\ell-1$, donc $\left|E_{k}\right|=2^{\ell-1}$. Enfin, puisque $\boldsymbol{n} \geqslant 3$, les ensembles ${1,2 \mathfrak{n}}$ et ${2,2 \mathfrak{n}}$ sont tous deux insommables, et n'appartiennent pas à $E_{2 n}$. On en déduit que

$$s_{2n}⩾2+\sum _{k=1}^{2n}\mid E_k\mid =2+\sum _{\mathrm{\ell }=1}^n\mid E_{2\mathrm{\ell }-1}\mid +\mid E_{2\mathrm{\ell }}\mid =2+2\sum _{\mathrm{\ell }=1}^n{2}^{\mathrm{\ell }-1}=2+2^{n+1}-2=2^{n+1}\mathrm{.}s\_\{2\; n\}\; \backslash geqslant\; 2+\backslash sum\_\{k=1\}^\{2\; n\}\backslash left|E\_\{k\}\backslash right|=2+\backslash sum\_\{\backslash ell=1\}^\{n\}\backslash left|E\_\{2\; \backslash ell-1\}\backslash right|+\backslash left|E\_\{2\; \backslash ell\}\backslash right|=2+2\; \backslash sum\_\{\backslash ell=1\}^\{n\}\; 2^\{\backslash ell-1\}=2+2^\{n+1\}-2=2^\{n+1\}\; .$$

Exercice 2. Soit $m$ et $n$ deux entiers naturels. Démontrer que $n!\neq m^{2}+2019$. Solution de l'exercice 2 Procédons par l'absurde, et supposons que l'on dispose de deux entiers naturels $m$ et $n$ tels que $n!=m^{2}+2019$. Tout d'abord, on sait que $n!\geqslant 2019>6!=720$, donc que $n \geqslant 7$. Par conséquent, $n!$ est divisible par $7!=2^{4} \times 3^{2} \times 5 \times 7$, et l'on a $0 \equiv m^{2}+2019$ $(\bmod 7!)$. En vertu de la décomposition en produit de facteurs premiers énoncée ci-dessus et du théorème Chinois, cela signifie que -2019 est un carré modulo $k$ pour tout entier $k$, parmi $2^{4}, 3^{2}$, 5 et 7 . On pourrait démontrer que cela ne constitue pas une contradiction pour $k=5$ et $k=7$. En revanche, -2019 n'est pas un carré modulo 9 (ni modulo 16). En effet, si m² $\equiv-2019 \equiv-3$ $(\bmod 9)$, alors 3 divise $m$, donc 9 divise $m^{2}$, qui devrait donc être congru à la fois à 0 et à -3 modulo 9. Ainsi, dès lors que $n \geqslant 7$, on a en fait $n!\equiv 0 \not \equiv m^{2}-3 \equiv m^{2}+2019(\bmod 9)$, ce qui montre bien que nulle paire d'entiers naturels ( $m, n$ ) ne peut satisfaire l'équation $n!=m^{2}+2019$. Note : On a également $-2019 \equiv 5(\bmod 8)$, alors que $n^{2} \equiv 1(\bmod 8)$ pour tout entier $n$ impair. Ainsi, comme prévu, -2019 n'est pas un carré modulo 8 , donc modulo $2^{4}$ non plus.

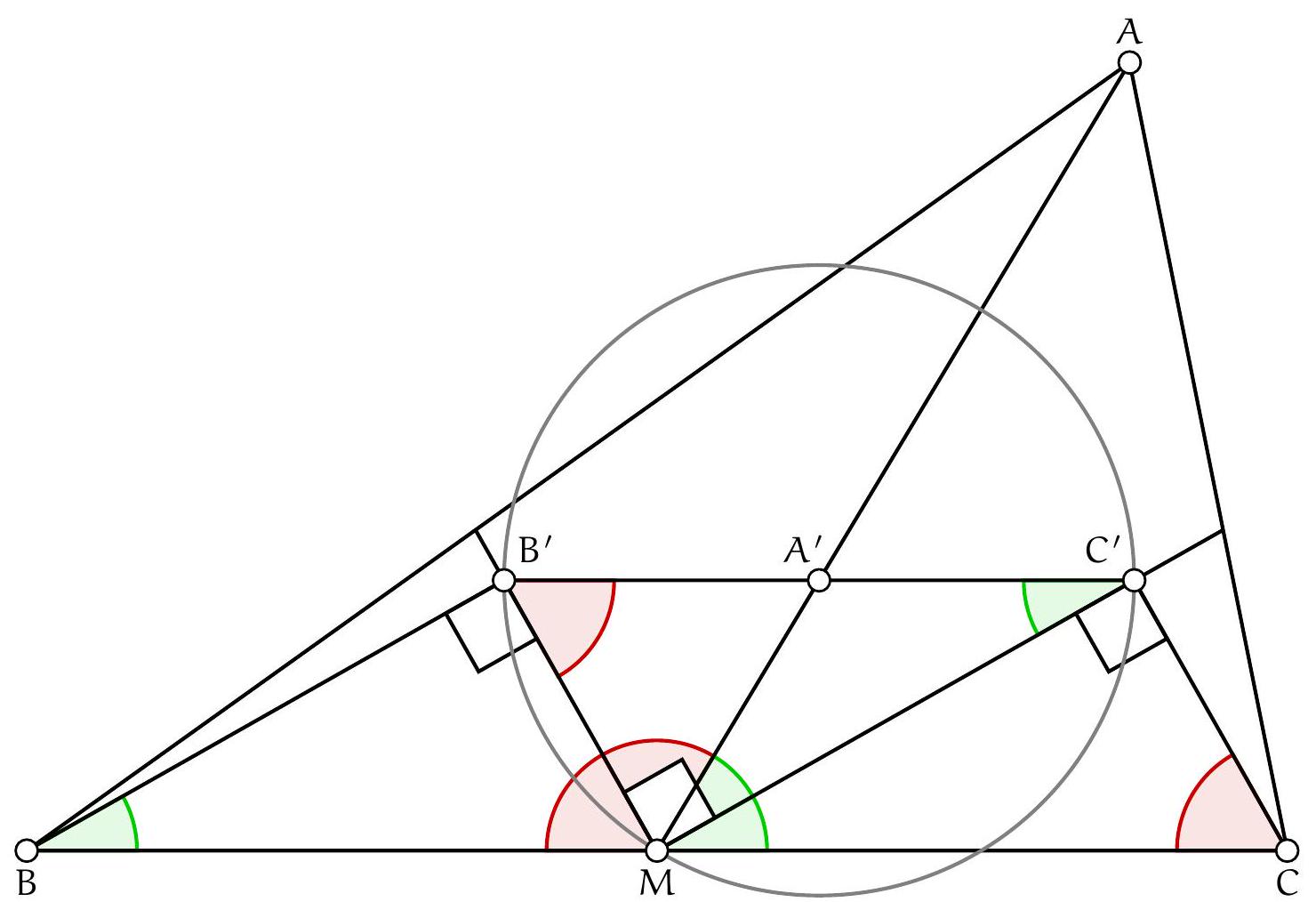
Exercice 3. Soit $A B C$ un triangle, et soit $M$ le pied de la médiane issue de $A$. Soit également $\ell_{\mathrm{b}}$ la bissectrice de $\widehat{A M B}$ et $\ell_{c}$ la bissectrice de $\widehat{A M C}$. Enfin, soit $B^{\prime}$ le projeté orthogonal de $B$ sur $\ell_{b}$, soit $C^{\prime}$ le projeté orthogonal de $C$ sur $\ell_{c}$, et soit $A^{\prime}$ le point $d^{\prime}$ intersection des droites $(A M)$ et ( $B^{\prime} C^{\prime}$ ). Démontrer que $A^{\prime} B^{\prime}=A^{\prime} C^{\prime}$. Solution de l'exercice 3 Soit $\beta$ l'angle $\widehat{A M B^{\prime}}$ et $\gamma$ l'angle $\widehat{A M C^{\prime}}$. Par construction, on sait que $2(\beta+\gamma)=180^{\circ}$, donc que $\widehat{\mathrm{B}^{\prime} \mathrm{MC}^{\prime}}=\beta+\gamma=90^{\circ}$. Ainsi, la droite $\ell_{\mathrm{b}}=\left(\mathrm{MB}^{\prime}\right)$ est perpendiculaire aux droites $\left(\mathrm{BB}^{\prime}\right)$ et $\ell_{c}=\left(M C^{\prime}\right)$, et la droite $\ell_{c}=\left(M C^{\prime}\right)$ est perpendiculaire aux droites $\left(C C^{\prime}\right)$ et $\ell_{b}=\left(M B^{\prime}\right)$. $D^{\prime}$ autre part, on remarque que $\widehat{\mathrm{B}^{\prime} \mathrm{BM}}=180^{\circ}-\widehat{\mathrm{BB}^{\prime} M}-\widehat{\mathrm{BMB}^{\prime}}=180^{\circ}-90^{\circ}-\beta=\gamma$ et que, de même, $\widehat{C^{\prime} C M}=\beta$. Ainsi, les deux triangles $B B^{\prime} M$ et $M C^{\prime} C$ sont semblables. En outre, puisque $M$ est le pied de la médiane de $A B C$ issue de $A$, $c^{\prime}$ est en fait le milieu de [BC], donc $B M=M C$. Les deux triangles $B B^{\prime} M$ et $M C C^{\prime}$ sont donc isométriques. En particulier, on en déduit que $B B^{\prime}=M C^{\prime}$ et que $C C^{\prime}=M B^{\prime}$. Mais alors, puisque le triangle $M B^{\prime} C^{\prime}$ est rectangle en $M$, il a un angle et deux côtés de mêmes mesures que le triangle $B^{\prime} M B$, et il est donc isométrique avec $B^{\prime} M B$ et avec $C^{\prime} C M$. On en déduit notamment que

$$\widehat{A^{\mathrm{\prime }}{C}^{\mathrm{\prime }}M}=\widehat{B^{\mathrm{\prime }}{C}^{\mathrm{\prime }}M}=\widehat{MB{B}^{\mathrm{\prime }}}=\gamma =\widehat{AM{C}^{\mathrm{\prime }}}=\widehat{A^{\mathrm{\prime }}M{C}^{\mathrm{\prime }}}\backslash widehat\{A^\{\backslash prime\}\; C^\{\backslash prime\}\; M\}=\backslash widehat\{B^\{\backslash prime\}\; C^\{\backslash prime\}\; M\}=\backslash widehat\{M\; B\; B^\{\backslash prime\}\}=\backslash gamma=\backslash widehat\{A\; M\; C^\{\backslash prime\}\}=\backslash widehat\{A^\{\backslash prime\}\; M\; C^\{\backslash prime\}\}$$

donc que le triangle $A^{\prime} C^{\prime} M$ est isocèle en $A^{\prime}$. De même, le triangle $A^{\prime} B^{\prime} M$ est isocèle en $A^{\prime}$, et on en conclut comme prévu que $A^{\prime} B^{\prime}=A^{\prime} M=A^{\prime} C^{\prime}$.

Exercice 4. Soit $\mathrm{f}: \mathbb{Z} \mapsto \mathbb{R}$ une fonction telle que

$$\mathbf{f}(\mathrm{n}+2)=(f(n+1)+\mathbf{f}(\mathrm{n}))\mathrm{/}2\backslash mathbf\{f\}(\backslash mathrm\{n\}+2)=(f(n+1)+\backslash mathbf\{f\}(\backslash mathrm\{n\}))\; /\; 2$$

pour tout entier $n$. On suppose que f est bornée, c'est-à-dire qu'il existe un réel $\mathbf{F}$ tel que $-F \leqslant f(n) \leqslant F$ pour tout $n$. Démontrer que $f$ est une fonction constante. Solution de l'exercice 4 Supposons que f n'est pas constante. Il existe donc un entier n et un réel $\varepsilon \neq 0$ tels que $f(n+1)-f(n)=\varepsilon$. Pour tout entier $k$, posons $\Delta_{k}=f(k+1)-f(k)$. Alors

$${\mathrm{\Delta }}_{k+1}=f(k+2)-f(k+1)=(f(k+1)+f(k))\mathrm{/}2-f(k+1)=-{\mathrm{\Delta }}_k\mathrm{/}2\backslash Delta\_\{k+1\}=f(k+2)-f(k+1)=(f(k+1)+f(k))\; /\; 2-f(k+1)=-\backslash Delta\_\{k\}\; /\; 2$$

et, réciproquement, $\Delta_{\mathrm{k}-1}=-2 \Delta_{\mathrm{k}}$. Une récurrence immédiate indique alors que $\Delta_{\mathrm{n}-\mathrm{k}}=$ $(-2)^{k} \varepsilon$ pour tout $k \geqslant 0$. Or, pour tout entier $k$, on sait que $\left|\Delta_{k}\right| \leqslant|\mathbf{f}(k+1)|+|f(k)| \leqslant 2 \mathbf{F}$. Mais ceci est incompatible avec le fait que $\left|\Delta_{n-k}\right|=2^{k}|\varepsilon|$ pout tout $k \geqslant 0$. Notre supposition initiale était donc absurde, et $f$ est bien constante.

Exercices du groupe Senior

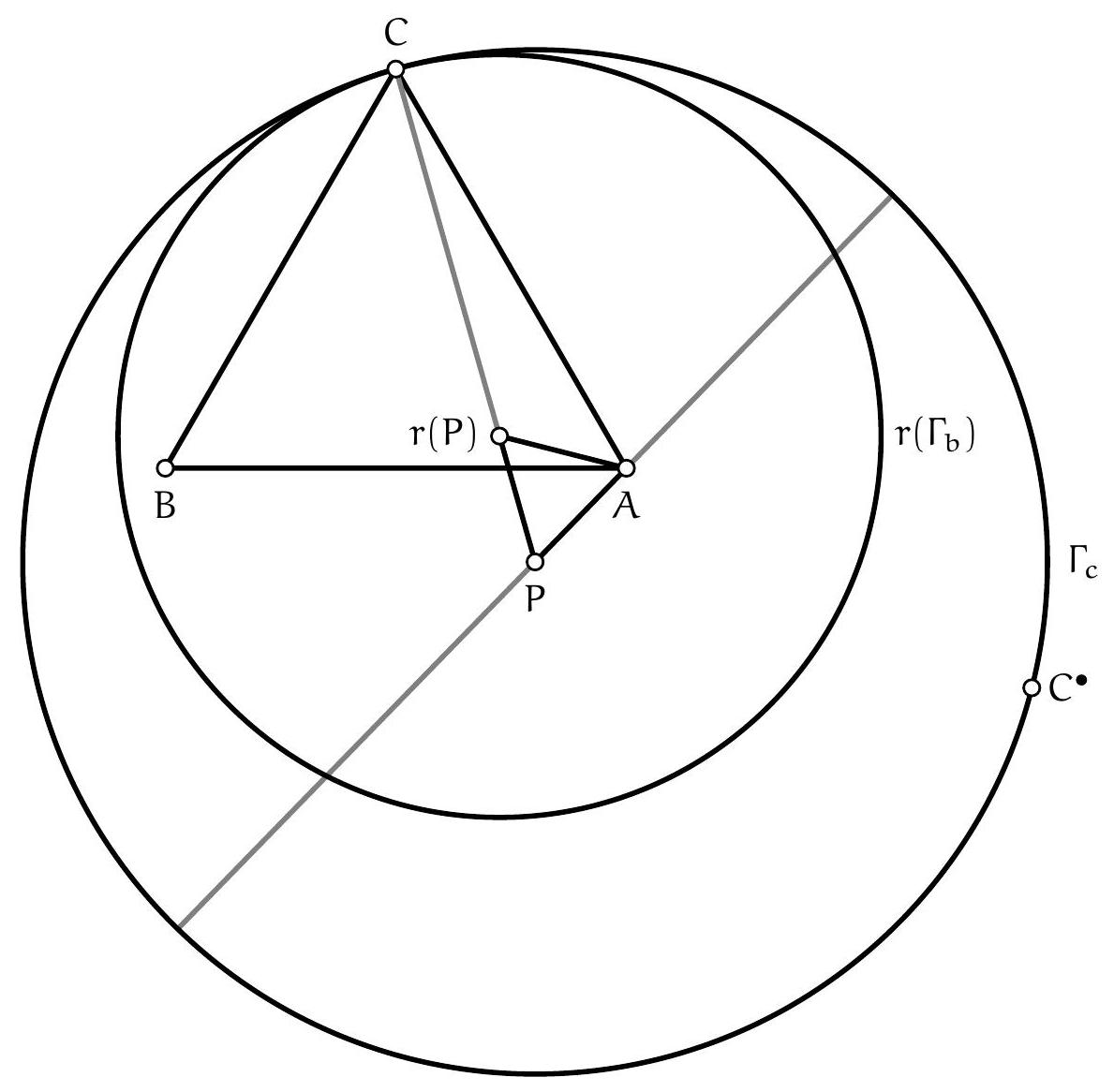
Exercice 5. Soit $A, B, C$ et $P$ quatre points du plan tels que $A B C$ soit un triangle équilatéral et que $A P<B P<C P$. On suppose que la seule donnée des longueurs $A P, B P$ et $C P$ nous permet de déterminer, de manière unique, la longueur $A B$. Démontrer que P appartient au cercle circonscrit à $A B C$. Solution de l'exercice 5 Soit $\Gamma_{\mathrm{a}}, \Gamma_{\mathrm{b}}$ et $\Gamma_{\mathrm{c}}$ les cercles de centre P et passant respectivement par $A$, $B$ et $C$. Soit également $C^{\bullet}$ le symétrique de $C$ par rapport à ( $A P$ ). Notons que $C^{\bullet}$ est le seul point de $\Gamma_{\mathrm{c}}$, autre que C lui-même, tel que $A C=A C^{\bullet}$. On note maintenant r la rotation de centre $\mathcal{A}$ et d'angle $60^{\circ}$ dans le sens horaire. Quitte à faire subir une symétrie à la figure de répart, on suppose que $C=r(B)$. Puis, à tout point $B^{\prime}$ de $\Gamma_{b}$, on associe le point $C^{\prime}=r\left(B^{\prime}\right)$. Le triangle $A B^{\prime} C^{\prime}$ est équilatéral, et l'hypothèse de l'énoncé stipule donc que, pour tout $B^{\prime}$, le point $C^{\prime}$ ne peut appartenir à $\Gamma_{c}$ que s'il est égal à $C$ ou à $C^{\bullet}$. Or, quand $B^{\prime}$ décrit $\Gamma_{b}$, le point $C^{\prime}$ décrit le cercle $r\left(\Gamma_{b}\right)$, de centre $r(P)$ et de rayon $P B$. Ce cercle ne peut contenir à la fois les points $C$ et $C^{\bullet}$, puisque alors son centre se trouverait sur la médiatrice (AP) de $\left[C^{\bullet}\right]$, ce qui n'est pas le cas de $r(P)$. Comme $\mathrm{r}\left(\Gamma_{\mathrm{b}}\right)$ contient déjà C , il ne peut donc pas contenir d'autre point de $\Gamma_{\mathrm{c}}$, et puisque $\mathrm{r}(\mathrm{P}) A=\mathrm{PA}<\mathrm{PB}$, on sait que $A$ est situé à l'intérieur $\operatorname{de} \mathrm{r}\left(\Gamma_{\mathrm{b}}\right)$, qui est donc tangent intérieurement, en le point $C$, à $\Gamma_{\mathrm{c}}$. Comme $P B=r(P) C<P C, c^{\prime}$ est en fait que les points $C, r(P)$ et $P$ sont alignés dans cet ordre. On en déduit que $P C=r(P) C+r(P) P=P B+P A$, ou encore que $C P \cdot A B=B P \cdot A C+A P$. $B C$. L'égalité de Ptolémée indique donc que les points $A, B, C$ et $P$ sont cocycliques, ce qui conclut.

Exercice 6. Soit $a_{0}, a_{1}, \ldots, a_{d}$ des entiers tels que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=1$. Pour tout entier $n \geqslant 1$, on pose

$$u_n=\sum _{k=0}^d{a}_k\phi (n+k)u\_\{n\}=\backslash sum\_\{k=0\}^\{d\}\; a\_\{k\}\; \backslash varphi(n+k)$$

Démontrer que 1 est le seul entier naturel divisant tous les entiers $u_{n}$. On rappelle que $\varphi(n+k)$ est le nombre d'entiers naturels $\ell<n+k$ tels que $\operatorname{PGCD}(\ell, n+k)=1$. Solution de l'exercice 6 Procédons par l'absurde, et supposons qu'il existe un nombre premier $p$ qui divise tous les entiers $u_{n}$. Tout d'abord, puisque $\varphi(1)=\varphi(2)=1$ et que $\varphi(\mathfrak{n})$ est pair pour tout $\mathfrak{n} \geqslant 2$, on remarque que $u_{1} \equiv a_{0}+a_{1}(\bmod 2)$ et que $u_{2} \equiv a_{0}(\bmod 2)$. Comme $a_{0}$ et $a_{1}$ sont premiers entre eux, les entiers $\mathfrak{u}{1}$ et $\mathfrak{u}{2}$ ne peuvent donc pas être pairs tous les deux, de sorte que $p \geqslant 3$. Soit alors $\delta$ le plus grand entier tel que $p$ ne divise pas $a_{\delta}$. Pour tout entier $n \geqslant 1$, on note $T_{n}$ le $\delta$-uplet $(\varphi(n), \varphi(n+1), \ldots, \varphi(n+\delta-1))$, considéré modulo $p$. Puisque $u_{n} \equiv 0(\bmod p)$, $c^{\prime}$ est que

$$\phi (n+\delta )\equiv -a_{\delta }^{-1}\sum _{k=0}^{\delta -1}{a}_k\phi (n+k)(p)\backslash varphi(n+\backslash delta)\; \backslash equiv-a\_\{\backslash delta\}^\{-1\}\; \backslash sum\_\{k=0\}^\{\backslash delta-1\}\; a\_\{k\}\; \backslash varphi(n+k)\; \backslash quad(\backslash bmod\; p)$$

Ainsi, si l'on note $\lambda:(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta} \mapsto(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta}$ la fonction définie par

$$\lambda :(x_0,x_1,\dots ,x_{\delta -1})\mapsto (x_1,x_2,\dots ,x_{\delta -1},-a_{\delta }^{-1}\sum _{k=0}^{\delta -1}{a}_k{x}_k)\backslash lambda:\backslash left(x\_\{0\},\; x\_\{1\},\; \backslash ldots,\; x\_\{\backslash delta-1\}\backslash right)\; \backslash mapsto\backslash left(x\_\{1\},\; x\_\{2\},\; \backslash ldots,\; x\_\{\backslash delta-1\},-a\_\{\backslash delta\}^\{-1\}\; \backslash sum\_\{k=0\}^\{\backslash delta-1\}\; a\_\{k\}\; x\_\{k\}\backslash right)$$

on a $\mathbf{T}{\mathfrak{n}+1}=\lambda\left(\mathbf{T}{\mathfrak{n}}\right)$. Or, d'après le principe des tiroirs, il existe deux entiers $k, \ell \geqslant 1$ tels que $\mathbf{T}{\mathrm{k}}=\mathbf{T}{\mathrm{k}+\ell}$. On a alors $\mathbf{T}{\mathbf{n}}=\mathbf{T}{\mathrm{n}+\ell}$ et $\varphi(\mathrm{n}) \equiv \varphi(\mathrm{n}+\ell)(\bmod p)$ pour tout $n \geqslant k$. On montre alors le lemme suivant : pour tous les entiers $a \geqslant 1$ et $b \geqslant 3$, il existe un nombre premier $q>a$ tel que $q \not \equiv 1(\bmod b)$. En effet, l'entier $m=\max {a, b}!-1$ est congru à -1 $(\bmod b)$, donc il admet nécessairement un facteur premier $q \not \equiv 1(\bmod b)$, et $q$ ne peut pas diviser $\mathrm{m}+1=\max {\mathrm{a}, \mathrm{b}}!$, donc $\mathrm{q}>\mathrm{a}$. En appliquant ce lemme deux fois de suite, on en déduit qu'il existe deux nombres premiers $q$ et $r$ tels que $q, r \not \equiv 1(\bmod p)$ et $q>r>k+\ell$. Mais alors $q$ est premier avec $\ell$, donc $q^{\varphi(\ell)} \equiv 1(\bmod \ell)$, et $\varphi\left(q^{\varphi(\ell)} n\right) \equiv \varphi(n)(\bmod p)$ pour tout $n \geqslant k$. Puisque $q>r \geqslant k$, on en déduit que

Comme $q, r \not \equiv 1(\bmod p), c^{\prime}$ est que $q^{\varphi(\ell)} \equiv(q-1) q^{\varphi(\ell)-1} \equiv 1(\bmod p)$, donc que $q^{\varphi(\ell)-1} \equiv 0$ $(\bmod p)$, ce qui est impossible. On a ainsi obtenu la contradiction souhaitée, ce qui conclut.

Note : On peut aussi faire appel au théorème de Dirichlet, qui affirme que, pour tous les entiers $a$ et $b$ premiers entre eux, il existe une infinité de nombres premiers $q \equiv a(\bmod b)$. Il existe alors des nombres premiers $q_{0}>q_{1}>\ldots>q_{d}>p+d$ congrus à $1(\bmod p)$. Puis, si on choisit $k \in{0,1}$ tel que $p$ ne divise pas $a_{k}$, il existe aussi un nombre premier $r$ tel que $r \equiv 2(\bmod p)$ et $r \equiv k-i\left(\bmod q_{i}\right)$ pour tout $i \neq k$. Alors $p$ ne divise pas $u_{r-k}$.

Exercice 7 . Soit $n \geqslant 2$ un entier. Clara dispose d'un plateau de taille $3 n \times 3 n$, semblable à un échiquier. Elle vient d'inventer une nouvelle pièce, le léopard, qu'elle peut mouvoir comme suit : en le déplaçant d'une case vers le haut, d'une case vers la droite, ou bien d'une case en diagonale, vers le bas et la gauche. Clara a posé son léopard sur une des cases du plateau, puis elle l'a déplacé, de sorte qu'il ne passe jamais deux fois par la même case, jusqu'à ce qu'il revienne à sa case de départ. Quelle est le plus grand nombre possible de déplacements que Clara a pu effectuer en procédant de la sorte?

Solution de l'exercice 7 Tout d'abord, Clara peut effectuer $9 \mathfrak{n}^{2}-3$ en procédant comme illustré ci-dessous dans le cas où $\mathrm{n}=3$.

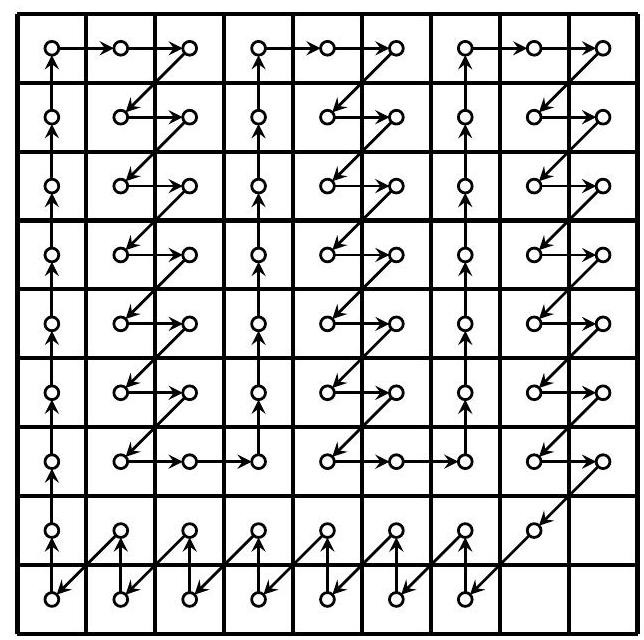
Montrons maintenant qu'elle ne peut pas mieux faire. Tout d'abord, on identifie chaque case en ligne $i$ (en partant du bas) et en colonne $j$ (en partant de la gauche) à la paire ( $i, j$ ), où $1 \leqslant i, j \leqslant 3 n$. Puis on colorie les cases du plateau de trois couleurs $C_{0}, C_{1}$ et $C_{2}$, en affectant à la case $(\mathfrak{i}, \mathfrak{j})$ la couleur $\mathrm{C}{\boldsymbol{i}+\boldsymbol{j}}(\bmod 3)$. Chaque mouvement du léopard consiste à se mouvoir d'un vecteur $(0,1),(1,0)$ ou $(-1,-1)$. Par conséquent, il passe systématiquement d'une case de couleur $C{k}$ à une case de couleur $C_{k+1}(\bmod 3)$. Il a donc effectué un nombre de déplacements divisible par 3, et il suffit de démontrer qu'il n'a pas pu passer par toutes les cases. À cette fin, remarquons que son parcours décrit un graphe planaire formé d'un seul cycle, qui contient donc une face interne (finie) et une face externe. Or, si le léopard est passé par la case $(1,3 \mathfrak{n})$, il a dû utiliser l'arête $(1,3 \mathfrak{n}) \rightarrow(2,3 \mathfrak{n})$, donc contourner sa face interne dans le sens horaire. Mais, de même, s'il est passé par la case ( $3 n, 1$ ), il a dû utiliser l'arête $(3 n, 1) \rightarrow(3 n, 2)$, donc contourner sa face interne dans le sens anti-horaire. Il n'a donc pas pu passer par ces deux cases lors du même trajet, ce qui conclut.

Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.